Гигантское магнитосопротивление

Явление, связанное с изменением проводимости в металлических слоях

Гигантское магнитосопротивление ( GMR ) — квантово-механический эффект магнитосопротивления, наблюдаемый в многослойных структурах , состоящих из чередующихся ферромагнитных и немагнитных проводящих слоев. Нобелевская премия по физике 2007 года была присуждена Альберту Ферту и Петеру Грюнбергу за открытие GMR, которое также заложило основу для изучения спинтроники .

Эффект наблюдается как существенное изменение электрического сопротивления в зависимости от того, находится ли намагниченность соседних ферромагнитных слоев в параллельном или антипараллельном выравнивании. Общее сопротивление относительно низкое для параллельного выравнивания и относительно высокое для антипараллельного выравнивания. Направление намагниченности можно контролировать, например, прикладывая внешнее магнитное поле. Эффект основан на зависимости рассеяния электронов от ориентации спина.

Основное применение GMR — в датчиках магнитного поля , которые используются для считывания данных с жестких дисков , биосенсоров , микроэлектромеханических систем (MEMS) и других устройств. ^[1] Многослойные структуры GMR также используются в магниторезистивной памяти с произвольным доступом (MRAM) в качестве ячеек, которые хранят один бит информации.

В литературе термин гигантское магнитосопротивление иногда путают с колоссальным магнитосопротивлением ферромагнитных и антиферромагнитных полупроводников, которое не связано с многослойной структурой. ^{[2] [3]}

Основополагающие результаты Альберта Ферта и Петера Грюнберга (1988): изменение сопротивления сверхрешеток Fe/Cr при 4,2 К во внешнем магнитном поле H. Ток и магнитное поле были параллельны оси [110] . Стрелка справа показывает максимальное изменение сопротивления. H _s — поле насыщения. ^{[примечание 1]}

Формулировка

Магнитосопротивление — зависимость электрического сопротивления образца от напряженности внешнего магнитного поля. Численно характеризуется величиной

${\displaystyle \delta _{H}={\frac {R(H)-R(0)}{R(0)}}}$

где R(H) — сопротивление образца в магнитном поле H, а R(0) соответствует H = 0. ^[4] Альтернативные формы этого выражения могут использовать электрическое удельное сопротивление вместо сопротивления, другой знак для δ _H , ^[5] и иногда нормализуются с помощью R(H), а не R(0). ^[6]

Термин «гигантское магнитосопротивление» указывает на то, что величина δ _H для многослойных структур значительно превышает анизотропное магнитосопротивление, имеющее типичное значение в пределах нескольких процентов. ^{[7] [8]}

История

GMR был открыт в 1988 году независимо ^{[9] [10]} группами Альберта Ферта из Университета Париж-Юг , Франция, и Петера Грюнберга из Исследовательского центра Юлих , Германия. Практическое значение этого экспериментального открытия было признано Нобелевской премией по физике, присужденной Ферту и Грюнбергу в 2007 году. ^[11]

Первые шаги

Первая математическая модель, описывающая влияние намагниченности на подвижность носителей заряда в твердых телах , связанную со спином этих носителей, была представлена ​​в 1936 году. Экспериментальные доказательства потенциального усиления δ _H известны с 1960-х годов. К концу 1980-х годов анизотропное магнитосопротивление было хорошо изучено, ^{[12] [13],} но соответствующее значение δ _H не превышало нескольких процентов. ^[7] Усиление δ _H стало возможным с появлением методов подготовки образцов, таких как молекулярно-лучевая эпитаксия , которая позволяет изготавливать многослойные тонкие пленки толщиной в несколько нанометров. ^[14]

Эксперимент и его интерпретация

Ферт и Грюнберг изучали электрическое сопротивление структур, включающих ферромагнитные и неферромагнитные материалы. В частности, Ферт работал над многослойными пленками, а Грюнберг в 1986 году открыл антиферромагнитное обменное взаимодействие в пленках Fe/Cr. ^[14]

Работа по открытию ГМС была выполнена двумя группами на немного разных образцах. Группа Ферта использовала сверхрешетки (001)Fe/(001) Cr, в которых слои Fe и Cr были нанесены в высоком вакууме на подложку (001) GaAs, поддерживаемую при 20 °C, а измерения магнитосопротивления проводились при низкой температуре (обычно 4,2 K). ^[10] Работа Грюнберга была выполнена на многослойных слоях Fe и Cr на (110) GaAs при комнатной температуре. ^[9]

В многослойных пленках Fe/Cr с толщиной слоев железа 3 нм увеличение толщины немагнитных слоев Cr с 0,9 до 3 нм ослабляло антиферромагнитную связь между слоями Fe и уменьшало поле размагничивания, которое также уменьшалось при нагревании образца от 4,2 К до комнатной температуры. Изменение толщины немагнитных слоев приводило к значительному уменьшению остаточной намагниченности в петле гистерезиса. Электрическое сопротивление изменялось до 50% при внешнем магнитном поле 4,2 К. Ферт назвал новый эффект гигантским магнитосопротивлением, чтобы подчеркнуть его отличие от анизотропного магнитосопротивления. ^{[10] [15]} Эксперимент Грюнберга ^[9] сделал то же самое открытие, но эффект был менее выраженным (3% по сравнению с 50%) из-за того, что образцы находились при комнатной температуре, а не при низкой температуре.

Первооткрыватели предположили, что эффект основан на спин-зависимом рассеянии электронов в сверхрешетке, в частности, на зависимости сопротивления слоев от относительной ориентации намагниченности и электронных спинов. ^{[9] [10]} Теория GMR для различных направлений тока была разработана в последующие несколько лет. В 1989 году Кэмли и Барнас рассчитали геометрию «тока в плоскости» (CIP), где ток течет вдоль слоев, в классическом приближении, ^[16] тогда как Леви и др. использовали квантовый формализм. ^[17] Теория GMR для тока, перпендикулярного слоям (ток, перпендикулярный плоскости или геометрия CPP), известная как теория Вале-Ферта, была представлена ​​в 1993 году. ^[18] Приложения предпочитают геометрию CPP ^[19], поскольку она обеспечивает большее отношение магнитосопротивления (δ _H ), ^[20] что приводит к большей чувствительности устройства. ^[21]

Теория

Основы

Рассеяние, зависящее от спина

Плотность электронных состояний (DOS) в магнитных и немагнитных металлах. 1: структура двух ферромагнитных и одного немагнитного слоев (стрелки указывают направление намагниченности). 2: расщепление DOS для электронов с различным направлением спина для каждого слоя (стрелки указывают направление спина). F: уровень Ферми . Магнитный момент антипараллелен направлению полного спина на уровне Ферми.

В магнитно-упорядоченных материалах электрическое сопротивление в значительной степени зависит от рассеяния электронов на магнитной подрешетке кристалла, образованной кристаллографически эквивалентными атомами с ненулевыми магнитными моментами. Рассеяние зависит от относительной ориентации электронных спинов и этих магнитных моментов: оно слабее всего, когда они параллельны, и сильнее всего, когда они антипараллельны; оно относительно сильно в парамагнитном состоянии, в котором магнитные моменты атомов имеют случайную ориентацию. ^{[7] [22]}

Для хороших проводников, таких как золото или медь, уровень Ферми лежит внутри sp- зоны, а d- зона полностью заполнена. В ферромагнетиках зависимость рассеяния электронов на атомах от ориентации их магнитных моментов связана с заполнением зоны, отвечающей за магнитные свойства металла, например, 3 d- зоны для железа , никеля или кобальта . D -зона ферромагнетиков расщеплена, так как содержит разное количество электронов со спинами, направленными вверх и вниз. Поэтому плотность электронных состояний на уровне Ферми также различна для спинов, направленных в противоположные стороны. Уровень Ферми для электронов с основным спином расположен внутри sp-зоны , и их транспорт аналогичен в ферромагнетиках и немагнитных металлах. Для электронов с неосновным спином sp- и d - зоны гибридизированы, и уровень Ферми лежит внутри d -зоны. Гибридизированная spd- зона имеет высокую плотность состояний, что приводит к более сильному рассеянию и, следовательно, к более короткому среднему свободному пробегу λ для спина меньшинства, чем для спина большинства. В никеле, легированном кобальтом, отношение λ _↑ /λ _↓ может достигать 20. ^[23]

Согласно теории Друде , проводимость пропорциональна λ, которая в тонких металлических пленках составляет от нескольких до нескольких десятков нанометров. Электроны «запоминают» направление спина в пределах так называемой длины релаксации спина (или длины диффузии спина), которая может значительно превышать длину свободного пробега. Спин-зависимый транспорт относится к зависимости электропроводности от направления спина носителей заряда. В ферромагнетиках он происходит за счет переходов электронов между нерасщепленной 4s и расщепленной 3d зонами. ^[7]

В некоторых материалах взаимодействие между электронами и атомами является самым слабым, когда их магнитные моменты антипараллельны, а не параллельны. Сочетание обоих типов материалов может привести к так называемому обратному эффекту GMR. ^{[7] [24]}

Зонная структура (слева) и плотность состояний (справа)

• 
  Медь (немагнитный металл). F – уровень Ферми. Вертикальная ось – энергия в эВ.
• 
  Кобальт (большинство спинов)
• 
  Кобальт (минорные спины)

Геометрии CIP и CPP

Спиновые клапаны в считывающей головке датчика в геометриях CIP (слева) и CPP (справа). Красный: провода, подающие ток на датчик, зеленый и желтый: ферромагнитные и немагнитные слои. V: разность потенциалов.

Электрический ток может передаваться через магнитные сверхрешетки двумя способами. В геометрии тока в плоскости (CIP) ток течет вдоль слоев, а электроды расположены с одной стороны структуры. В конфигурации тока перпендикулярно плоскости (CPP) ток передается перпендикулярно слоям, а электроды расположены с разных сторон сверхрешетки. ^[7] Геометрия CPP приводит к более чем вдвое более высокому GMR, но ее сложнее реализовать на практике, чем конфигурацию CIP. ^{[25] [26]}

Транспорт носителей через магнитную сверхрешетку

Спиновый клапан на основе эффекта GMR. FM: ферромагнитный слой (стрелки указывают направление намагниченности), NM: немагнитный слой. Электроны со спинами вверх и вниз рассеиваются в клапане по-разному.

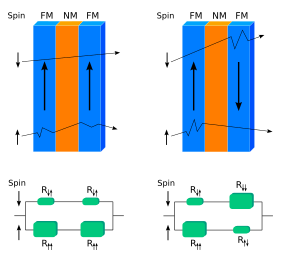
Магнитное упорядочение различается в сверхрешетках с ферромагнитным и антиферромагнитным взаимодействием между слоями. В первом случае направления намагниченности одинаковы в разных ферромагнитных слоях при отсутствии приложенного магнитного поля, тогда как во втором случае противоположные направления чередуются в многослойной структуре. Электроны, проходящие через ферромагнитную сверхрешетку, взаимодействуют с ней гораздо слабее, когда направления их спинов противоположны намагниченности решетки, чем когда они параллельны ей. Для антиферромагнитной сверхрешетки такая анизотропия не наблюдается; в результате она рассеивает электроны сильнее, чем ферромагнитная сверхрешетка, и обладает более высоким электрическим сопротивлением. ^[7]

Применение эффекта GMR требует динамического переключения между параллельной и антипараллельной намагниченностью слоев в сверхрешетке. В первом приближении плотность энергии взаимодействия между двумя ферромагнитными слоями, разделенными немагнитным слоем, пропорциональна скалярному произведению их намагниченностей:

${\displaystyle w=-J(\mathbf {M} _{1}\cdot \mathbf {M} _{2}).}$

Коэффициент J является осциллирующей функцией толщины немагнитного слоя d _s ; поэтому J может менять свою величину и знак. Если значение d _s соответствует антипараллельному состоянию, то внешнее поле может переключить сверхрешетку из антипараллельного состояния (высокое сопротивление) в параллельное состояние (низкое сопротивление). Полное сопротивление структуры можно записать как

${\displaystyle R=R_{0}+\Delta R\sin ^{2}{\frac {\theta }{2}},}$

где R ₀ — сопротивление ферромагнитной сверхрешетки, ΔR — приращение ГМС, а θ — угол между намагниченностями соседних слоев. ^[25]

Математическое описание

Явление GMR можно описать с помощью двух каналов проводимости, связанных со спином, соответствующих проводимости электронов, для которых сопротивление минимально или максимально. Связь между ними часто определяется через коэффициент спиновой анизотропии β. Этот коэффициент можно определить с помощью минимума и максимума удельного электрического сопротивления ρ _F± для спин-поляризованного тока в виде

${\displaystyle \rho _{F\pm }={\frac {2\rho _{F}}{1\pm \beta }},}$

где ρ _F — среднее удельное сопротивление ферромагнетика. ^[27]

Модель резистора для структур CIP и CPP

Если рассеяние носителей заряда на границе раздела ферромагнитного и немагнитного металла мало, а направление спинов электронов сохраняется достаточно долго, то удобно рассмотреть модель, в которой полное сопротивление образца представляет собой сумму сопротивлений магнитного и немагнитного слоев.

В этой модели имеются два канала проводимости для электронов с различным направлением спина относительно намагниченности слоев. Поэтому эквивалентная схема структуры GMR состоит из двух параллельных соединений, соответствующих каждому из каналов. В этом случае GMR можно выразить как

${\displaystyle \delta _{H}={\frac {\Delta R}{R}}={\frac {R_{\uparrow \downarrow }-R_{\uparrow \uparrow }}{R_{\uparrow \uparrow }}}={\frac {(\rho _{F+}-\rho _{F-})^{2}}{(2\rho _{F+}+\chi \rho _{N})(2\rho _{F-}+\chi \rho _{N})}}.}$

Здесь индекс R обозначает коллинеарную и противоположно ориентированную намагниченность в слоях, χ = b/a — отношение толщин магнитного и немагнитного слоев, а ρ _N — удельное сопротивление немагнитного металла. Это выражение применимо как для структур CIP, так и для структур CPP. При условии это соотношение можно упростить, используя коэффициент спиновой асимметрии ${\displaystyle \chi \rho _{N}\ll \rho _{F\pm }}$

${\displaystyle \delta _{H}={\frac {\beta ^{2}}{1-\beta ^{2}}}.}$

Такое устройство, сопротивление которого зависит от ориентации электронного спина, называется спиновым клапаном . Он «открыт», если намагниченности его слоев параллельны, и «закрыт» в противном случае. ^[28]

Модель Валета-Ферта

В 1993 году Тьерри Вале и Альбер Ферт представили модель гигантского магнитосопротивления в геометрии CPP, основанную на уравнениях Больцмана. В этой модели химический потенциал внутри магнитного слоя разделяется на две функции, соответствующие электронам со спинами, параллельными и антипараллельными намагниченности слоя. Если немагнитный слой достаточно тонкий, то во внешнем поле E ₀ поправки к электрохимическому потенциалу и полю внутри образца примут вид

${\displaystyle \Delta \mu ={\frac {\beta }{1-\beta ^{2}}}eE_{0}\ell _{s}e^{z/\ell _{s}},}$

${\displaystyle \Delta E={\frac {\beta ^{2}}{1-\beta ^{2}}}eE_{0}\ell _{s}e^{z/\ell _{s}},}$

где ℓ _s — средняя длина спиновой релаксации, а координата z отсчитывается от границы между магнитным и немагнитным слоями (z < 0 соответствует ферромагнетику). ^[18] Таким образом, электроны с большим химическим потенциалом будут накапливаться на границе ферромагнетика. ^[29] Это можно представить потенциалом накопления спинов V _AS или так называемым интерфейсным сопротивлением (присущим границе между ферромагнетиком и немагнитным материалом)

${\displaystyle R_{i}={\frac {\beta (\mu _{\uparrow \downarrow }-\mu _{\uparrow \uparrow })}{2ej}}={\frac {\beta ^{2}\ell _{sN}\rho _{N}}{1+(1-\beta ^{2})\ell _{sN}\rho _{N}/(\ell _{sF}\rho _{F})}},}$

где j — плотность тока в образце, ℓ _sN и ℓ _sF — длина спиновой релаксации в немагнитном и магнитном материалах соответственно. ^[30]

Подготовка устройства

Материалы и экспериментальные данные

Многие комбинации материалов демонстрируют ГМС ^[31] , наиболее распространенными являются следующие:

• FeCr ^[10]
• Co ₁₀ Cu ₉₀ : δ _H = 40% при комнатной температуре ^[32]
• [110]Co ₉₅ Fe ₅ /Cu: δ _H = 110% при комнатной температуре. ^[31]

Магнитосопротивление зависит от многих параметров, таких как геометрия устройства (CIP или CPP), его температура и толщина ферромагнитных и немагнитных слоев. При температуре 4,2 К и толщине слоев кобальта 1,5 нм увеличение толщины слоев меди d _Cu от 1 до 10 нм уменьшило δ _H с 80 до 10% в геометрии CIP. Между тем, в геометрии CPP максимум δ _H (125%) наблюдался при d _Cu = 2,5 нм, а увеличение d _Cu до 10 нм уменьшило δ _H до 60% осциллирующим образом. ^[33]

При нагревании сверхрешетки Co(1,2 нм)/Cu(1,1 нм) от температуры, близкой к нулю, до 300 К ее δ _H уменьшилась с 40 до 20% в геометрии CIP и со 100 до 55% в геометрии CPP. ^[34]

Немагнитные слои могут быть неметаллическими. Например, δ _H до 40% было продемонстрировано для органических слоев при 11 К. ^[35] Графеновые спиновые клапаны различных конструкций показали δ _H около 12% при 7 К и 10% при 300 К, что намного ниже теоретического предела 109%. ^[36]

Эффект GMR может быть усилен спиновыми фильтрами, которые отбирают электроны с определенной ориентацией спина; они сделаны из металлов, таких как кобальт. Для фильтра толщиной t изменение проводимости ΔG может быть выражено как

${\displaystyle \Delta G=\Delta G_{SV}+\Delta G_{f}(1-e^{\beta t/\lambda }),}$

где ΔG _SV — изменение проводимости спинового клапана без фильтра, ΔG _f — максимальное увеличение проводимости с фильтром, а β — параметр материала фильтра. ^[37]

Типы СВМР

GMR часто классифицируют по типу устройств, которые проявляют этот эффект. ^[38]

Фильмы

Антиферромагнитные сверхрешетки

GMR в пленках впервые наблюдали Ферт и Грюнберг при изучении сверхрешеток, состоящих из ферромагнитных и немагнитных слоев. Толщина немагнитных слоев была выбрана таким образом, чтобы взаимодействие между слоями было антиферромагнитным, а намагниченность в соседних магнитных слоях была антипараллельной. Тогда внешнее магнитное поле могло сделать векторы намагниченности параллельными, тем самым влияя на электрическое сопротивление структуры. ^[10]

Магнитные слои в таких структурах взаимодействуют посредством антиферромагнитной связи, что приводит к осциллирующей зависимости ГМС от толщины немагнитного слоя. В первых датчиках магнитного поля, использующих антиферромагнитные сверхрешетки, поле насыщения было очень большим, до десятков тысяч эрстед , из-за сильного антиферромагнитного взаимодействия между их слоями (изготовленными из хрома, железа или кобальта) и сильных полей анизотропии в них. Поэтому чувствительность приборов была очень низкой. Использование пермаллоя для магнитных и серебра для немагнитных слоев снизило поле насыщения до десятков эрстед. ^[39]

Спиновые клапаны, использующие обменное смещение

В наиболее успешных спиновых клапанах эффект GMR возникает из-за обменного смещения. Они включают в себя чувствительный слой, «фиксированный» слой и антиферромагнитный слой. Последний слой замораживает направление намагничивания в «фиксированном» слое. Чувствительный и антиферромагнитный слои сделаны тонкими, чтобы уменьшить сопротивление структуры. Клапан реагирует на внешнее магнитное поле, изменяя направление намагничивания в чувствительном слое относительно «фиксированного» слоя. ^[39]

Основным отличием этих спиновых клапанов от других многослойных ГМР-устройств является монотонная зависимость амплитуды эффекта от толщины d _N немагнитных слоев:

${\displaystyle \delta _{H}(d_{N})=\delta _{H0}{\frac {\exp \left(-d_{N}/\lambda _{N}\right)}{1+d_{N}/d_{0}}},}$

где δ _H0 — константа нормировки, λ _N — длина свободного пробега электронов в немагнитном материале, d ₀ — эффективная толщина, включающая взаимодействие между слоями. ^{[38] [40]} Зависимость от толщины ферромагнитного слоя можно задать как:

${\displaystyle \delta _{H}(d_{F})=\delta _{H1}{\frac {1-\exp \left(-d_{F}/\lambda _{F}\right)}{1+d_{F}/d_{0}}}.}$

Параметры имеют то же значение, что и в предыдущем уравнении, но теперь они относятся к ферромагнитному слою. ^[31]

Невзаимодействующие мультислои (псевдоспиновые клапаны)

GMR также может наблюдаться при отсутствии антиферромагнитных связующих слоев. В этом случае магнитосопротивление возникает из-за различий в коэрцитивных силах (например, для пермаллоя оно меньше, чем для кобальта). В многослойных материалах, таких как пермаллой/Cu/Co/Cu, внешнее магнитное поле переключает направление намагниченности насыщения на параллельное в сильных полях и на антипараллельное в слабых полях. Такие системы демонстрируют более низкое поле насыщения и большую δ _H, чем сверхрешетки с антиферромагнитной связью. ^[39] Похожий эффект наблюдается в структурах Co/Cu. Существование этих структур означает, что GMR не требует межслоевой связи и может возникать из-за распределения магнитных моментов, которые могут контролироваться внешним полем. ^[41]

Обратный эффект ГМС

В обратном GMR сопротивление минимально при антипараллельной ориентации намагниченности в слоях. Обратный GMR наблюдается, когда магнитные слои состоят из разных материалов, таких как NiCr/Cu/Co/Cu. Удельное сопротивление для электронов с противоположными спинами можно записать как ; оно имеет разные значения, т. е. разные коэффициенты β, для электронов со спином вверх и спином вниз. Если слой NiCr не слишком тонкий, его вклад может превышать вклад слоя Co, что приводит к обратному GMR. ^[24] Обратите внимание, что инверсия GMR зависит от знака произведения коэффициентов β в соседних ферромагнитных слоях, но не от знаков отдельных коэффициентов. ^[34] ${\displaystyle \rho _{\uparrow ,\downarrow }={\frac {2\rho _{F}}{1\pm \beta }}}$

Обратный ГМС также наблюдается, если сплав NiCr заменить на никель, легированный ванадием, но не при легировании никеля железом, кобальтом, марганцем, золотом или медью. ^[42]

GMR в зернистых структурах

ГМС в гранулированных сплавах ферромагнитных и немагнитных металлов был открыт в 1992 году и впоследствии объяснен спин-зависимым рассеянием носителей заряда на поверхности и в объеме зерен. Зерна образуют ферромагнитные кластеры диаметром около 10 нм, внедренные в немагнитный металл, образуя своего рода сверхрешетку. Необходимым условием для эффекта ГМС в таких структурах является плохая взаимная растворимость в его компонентах (например, кобальте и меди). Их свойства сильно зависят от температуры измерения и отжига. Они также могут демонстрировать обратный ГМС. ^{[32] [43]}

Приложения

Датчики спин-клапана

Общий принцип

Копия датчика GMR, разработанного Петером Грюнбергом

Одним из основных применений материалов GMR являются датчики магнитного поля, например, в жестких дисках ^[25] и биосенсорах, ^[31] , а также детекторы колебаний в MEMS. ^[31] Типичный датчик на основе GMR состоит из семи слоев:

1. Кремниевая подложка,
2. Связующий слой,
3. Чувствительный (нефиксированный) слой,
4. Немагнитный слой,
5. Фиксированный слой,
6. Антиферромагнитный (закрепляющий) слой,
7. Защитный слой.

Связующий и защитные слои часто изготавливаются из тантала , а типичным немагнитным материалом является медь. В чувствительном слое намагниченность может быть переориентирована внешним магнитным полем; он обычно изготавливается из сплавов NiFe или кобальта. Для антиферромагнитного слоя можно использовать FeMn или NiMn. Фиксированный слой изготавливается из магнитного материала, такого как кобальт. Такой датчик имеет асимметричную петлю гистерезиса из-за наличия магнитно-жесткого фиксированного слоя. ^{[44] [45]}

Спиновые клапаны могут проявлять анизотропное магнитосопротивление, что приводит к асимметрии кривой чувствительности. ^[46]

Жесткие диски

В жестких дисках (HDD) информация кодируется с помощью магнитных доменов , и изменение направления их намагниченности связано с уровнем логической 1, а отсутствие изменения соответствует логическому 0. Существует два метода записи: продольный и перпендикулярный.

В продольном методе намагниченность перпендикулярна поверхности. Между доменами образуется переходная область (доменные стенки), в которой магнитное поле выходит из материала. Если доменная стенка расположена на границе двух доменов северного полюса, то поле направлено наружу, а для двух доменов южного полюса оно направлено внутрь. Чтобы определить направление магнитного поля над доменной стенкой, направление намагниченности фиксируется перпендикулярно поверхности в антиферромагнитном слое и параллельно поверхности в чувствительном слое. Изменение направления внешнего магнитного поля отклоняет намагниченность в чувствительном слое. Когда поле стремится выровнять намагниченности в чувствительном и фиксированном слоях, электрическое сопротивление датчика уменьшается, и наоборот. ^[47]

Магнитная оперативная память

Использование спинового клапана в MRAM. 1: спиновый клапан как ячейка памяти (стрелки указывают на наличие ферромагнитных слоев), 2: строка, 3: столбец. Эллипсы со стрелками обозначают линии магнитного поля вокруг строк и столбцов при протекании через них электрического тока.

Ячейка магниторезистивной памяти с произвольным доступом (MRAM) имеет структуру, похожую на спин-клапанный датчик. Значение хранимых битов может быть закодировано через направление намагничивания в слое датчика; оно считывается путем измерения сопротивления структуры. Преимуществами данной технологии являются независимость от источника питания (информация сохраняется при отключении питания за счет потенциального барьера для переориентации намагниченности), низкое энергопотребление и высокая скорость. ^[25]

В типичном накопителе на основе GMR структура CIP расположена между двумя проводами, ориентированными перпендикулярно друг другу. Эти проводники называются линиями строк и столбцов. Импульсы электрического тока, проходящие по линиям, создают вихревое магнитное поле, которое влияет на структуру GMR. Линии поля имеют эллипсоидную форму, а направление поля (по часовой стрелке или против часовой стрелки) определяется направлением тока в линии. В структуре GMR намагниченность ориентирована вдоль линии.

Направление поля, создаваемого линией столбца, практически параллельно магнитным моментам, и оно не может их переориентировать. Линия ряда перпендикулярна и независимо от величины поля может повернуть намагниченность всего на 90°. При одновременном прохождении импульсов по линиям ряда и столбца, суммарное магнитное поле в месте расположения структуры ГМС будет направлено под острым углом по отношению к одним точкам и под тупым по отношению к другим. Если величина поля превысит некоторое критическое значение, последнее изменит свое направление.

Существует несколько методов хранения и считывания для описанной ячейки. В одном методе информация хранится в чувствительном слое; она считывается посредством измерения сопротивления и стирается при считывании. В другой схеме информация хранится в фиксированном слое, что требует более высоких токов записи по сравнению с токами считывания. ^[48]

Туннельное магнитосопротивление (TMR) является расширением спин-клапанного GMR, в котором электроны перемещаются со спинами, ориентированными перпендикулярно слоям через тонкий изолирующий туннельный барьер (заменяющий неферромагнитную прокладку). Это позволяет достичь большего импеданса, большего значения магнитосопротивления (~10× при комнатной температуре) и незначительной температурной зависимости. TMR теперь заменил GMR в MRAM и дисковых накопителях , в частности, для высокой плотности площади и перпендикулярной записи. ^[49]

Другие приложения

Магниторезистивные изоляторы для бесконтактной передачи сигнала между двумя электрически изолированными частями электрических цепей были впервые продемонстрированы в 1997 году как альтернатива оптоизоляторам . Мост Уитстона из четырех идентичных GMR-устройств нечувствителен к однородному магнитному полю и реагирует только тогда, когда направления поля антипараллельны в соседних плечах моста. Такие устройства были описаны в 2003 году и могут использоваться в качестве выпрямителей с линейной частотной характеристикой. ^[31]

Примечания

1. Эта схема не включает гистерезис, поскольку форма его петли в сверхрешетках сильно зависит от толщины немагнитного слоя d. Ферт наблюдал явный гистерезис с полем насыщения ~4 кГс и остаточной намагниченностью 60% от значения насыщения при d _Cu =1,8 нм. Когда d _Cu уменьшалось до 0,9 нм, GMR достигало максимума, но петля гистерезиса разрушалась; поле насыщения увеличивалось до 20 кГс, но остаточное поле было очень малым. (Baibich et al. 1988)

Цитаты

1. Рейг, Кардосо и Мукхопадьяй, 2013.
2. Нагаев, Э. Л. (1996). «Лантаноманганиты и другие магнитные проводники с гигантским магнитосопротивлением». Успехи физических наук . 166 (8): 833–858. doi :10.3367/UFNr.0166.199608b.0833.
3. Raveau, B.; Rao, CNR, ред. (1998). Колоссальное магнитосопротивление, упорядочение зарядов и связанные с этим свойства оксидов марганца . World Scientific Publishing Co. стр. 2. ISBN 978-981-02-3276-4.
4. Хирота, Э.; Иномата, К. (2002a). Гигантские магниторезистивные устройства . Springer. стр. 30. ISBN 978-3-540-41819-1.
5. Никитин, С.А. (2004). «Гигантское магнитосопротивление» (PDF) . Соросовский обозревательный журнал . 8 (2): 92–98.^{[ постоянная мертвая ссылка ]}
6. Пиппард, Альфред Брайан (2009). Магнитосопротивление в металлах . Кембриджские исследования по физике низких температур. Т. 2. Издательство Кембриджского университета. С. 8. ISBN 978-052111880-4.
7. Шапперт, Клод; Ферт, Альберт; Нгуен Ван Дау, Фредерик (2007). «Возникновение спиновой электроники в хранении данных». Nature Materials . 6 (11): 813–823. Bibcode :2007NatMa...6..813C. doi :10.1038/nmat2024. PMID  17972936. S2CID  21075877.
8. Хирота, Э.; Иномата, К. (2002b). Гигантские магниторезистивные устройства . Springer. стр. 23. ISBN 978-3-540-41819-1.
9. Бинаш, Г.; Грюнберг; Зауренбах; Цинн (1989). «Повышенное магнитосопротивление в слоистых магнитных структурах с антиферромагнитным межслойным обменом». Physical Review B. 39 ( 7): 4828–4830. Bibcode : 1989PhRvB..39.4828B. doi : 10.1103/PhysRevB.39.4828 . PMID  9948867.
10. Байбич и др. 1988.
11. "Нобелевская премия по физике 2007 года". Nobel Foundation . Архивировано из оригинала 5 августа 2011 года . Получено 27 февраля 2011 года .
12. Seitz, Frederick; Turnbull, David (1957). Advances in Research and Applications . Solid State Physics. Vol. 5. Academic Press. p. 31. ISBN 978-012607705-6.
13. Aboaf, JA (9 октября 1984 г.). «Новые магниторезистивные материалы». Патент США 4476454. Получено 11 апреля 2011 г.^{[ постоянная мертвая ссылка ]}
14. Fert, А. (2008a). "Нобелевская лекция: происхождение, развитие и будущее спинтроники*". Rev. Mod. Phys . 80 (4): 1517–1530. Bibcode :2008RvMP...80.1517F. doi : 10.1103/RevModPhys.80.1517 . Ферт, А. (2008б). «Происхождение, развитие и будущее спинтроники». Успехи физических наук . 178 (12): 1336–1348. doi :10.3367/UFNr.0178.200812f.1336.(Перепечатка Нобелевской лекции 2007 года от 8 декабря 2007 г.
15. Цымбал и Петтифор 2001, с. 120.
16. Camley, RE; Barnaś, J. (1989). «Теория эффектов гигантского магнитосопротивления в магнитных слоистых структурах с антиферромагнитной связью». Phys. Rev. Lett . 63 (6): 664–667. Bibcode :1989PhRvL..63..664C. doi :10.1103/PhysRevLett.63.664. PMID  10041140.
17. Ферт, Альберт; Леви, Питер М.; Чжан, Шуфэн (1990). «Электропроводность магнитных многослойных структур». Phys. Rev. Lett . 65 (13): 1643–1646. Bibcode : 1990PhRvL..65.1643L. doi : 10.1103/PhysRevLett.65.1643. PMID  10042322.
18. Valet, T.; Fert, A. (1993). "Теория перпендикулярного магнитосопротивления в магнитных многослойных материалах". Physical Review B. 48 ( 10): 7099–7113. Bibcode :1993PhRvB..48.7099V. doi :10.1103/PhysRevB.48.7099. PMID  10006879.
19. Нагасака, К. (30 июня 2005 г.). "Технология CPP-GMR для будущей высокоплотной магнитной записи" (PDF) . Fujitsu . Архивировано из оригинала (PDF) 6 августа 2008 г. . Получено 11 апреля 2011 г. .
20. Синдзё 2009.
21. Бушоу 2005, стр. 580.
22. Цымбал и Петтифор 2001, с. 122.
23. Цымбал и Петтифор 2001, стр. 126–132.
24. Buschow 2005, стр. 254.
25. Хвальковский А. В. «Гигантское магнитосопротивление: от открытия до Нобелевской премии». АМТ&К. Архивировано из оригинала 8 января 2015 года . Проверено 27 февраля 2011 г.
26. Басс, Дж.; Пратт, ВП (1999б). «Токово-перпендикулярное (CPP) магнитосопротивление в магнитных металлических многослойных материалах». Журнал магнетизма и магнитных материалов . 200 (1–3): 274–289. Bibcode : 1999JMMM..200..274B. doi : 10.1016/S0304-8853(99)00316-9.
27. Третьяк, Львов и Барабанов 2002, с. 243.
28. Третьяк, Львов и Барабанов 2002, стр. 258–261, 247–248.
29. Штер, Дж.; Зигманн, ХК (2006a). Магнетизм: от основ к наномасштабной динамике . Шпрингер-Верлаг Берлин Гейдельберг. п. 641. ИСБН 978-354030282-7.
30. Штер, Дж.; Зигманн, ХК (2006b). Магнетизм: от основ к наномасштабной динамике . Шпрингер-Верлаг Берлин Гейдельберг. стр. 648–649. ISBN 978-354030282-7.
31. Coehoorn, R. (2003). "Novel Magnetoelectronic Materials and Devices" (PDF) . Гигантское магнитосопротивление и магнитные взаимодействия в спиновых клапанах с обменным смещением. Lecture Notes . Technische Universiteit Eindhoven. Архивировано из оригинала (PDF) 24 июля 2011 г. . Получено 25 апреля 2011 г. .
32. Грановский, AB; Ильин, M.; Жуков, A.; Жукова, V.; Гонсалес, J. (2011). "Гигантское магнитосопротивление гранулярных микропроводов: спин-зависимое рассеяние в интегранулярных прокладках" (PDF) . Физика твердого тела . 53 (2): 320–322. Bibcode :2011PhSS...53..320G. doi :10.1134/S1063783411020107. S2CID  119767942.
33. Бушоу 2005, стр. 248.
34. Bass, J.; Pratt, WP (1999a). "Токово-перпендикулярное (CPP) магнитосопротивление в магнитных металлических многослойных материалах". Журнал магнетизма и магнитных материалов . 200 (1–3): 274–289. Bibcode : 1999JMMM..200..274B. doi : 10.1016/S0304-8853(99)00316-9.
35. Сан, Дали; Инь, Л; Сан, К; Го, Х; Гай, З; Чжан, ХГ; Уорд, ТЗ; Чэн, З; Шен, Дж (2010). «Гигантское магнитосопротивление в органических спиновых клапанах». Physical Review Letters . 104 (23): 236602. Bibcode : 2010PhRvL.104w6602S. doi : 10.1103/PhysRevLett.104.236602 . PMID  20867259.
36. Цинь, Руи; Лу, Цзин; Лай, Лин; Чжоу, Цзин; Ли, Хун; Лю, Цихан; Ло, Гуанфу; Чжао, Лина; Гао, Чжэнсян; Мэй, Вай Нин; Ли, Гуанпин (2010). «Гигантское магнитосопротивление при комнатной температуре более одного миллиарда процентов в устройстве из голых графеновых нанолент». Физ. Преподобный Б. 81 (23): 233403. Бибкод : 2010PhRvB..81w3403Q. doi : 10.1103/PhysRevB.81.233403.
37. Бланд, Дж. А. Ц.; Хайнрих, Б., ред. (2005). Ультратонкие магнитные структуры . Применение наномагнетизма. Т. IV. Springer. С. 161–163. ISBN 978-3-540-21954-5.
38. Tsymbal, Evgeny. "GMR Structures". Университет Небраски-Линкольна. Архивировано из оригинала 12 декабря 2012 года . Получено 11 апреля 2011 года .
39. Nalwa, Hari Singh (2002a). Справочник по тонкопленочным материалам: Наноматериалы и магнитные тонкие пленки . Том 5. Academic Press. С. 518–519. ISBN 978-012512908-4.
40. Налва, Хари Сингх (2002b). Справочник по тонкопленочным материалам: Наноматериалы и магнитные тонкие пленки . Том 5. Academic Press. С. 519, 525–526. ISBN 978-012512908-4.
41. Pu, FC (1996). Shang, CH; Wang, YJ (ред.). Аспекты современного магнетизма: Конспект лекций Восьмой китайской международной летней школы физики Пекин, Китай 28 августа-7 сентября 1995 г. World Scientific. стр. 122. ISBN 978-981022601-5.
42. Гимарайнш, Альберто П. (2009). Принципы наномагнетизма . Спрингер. п. 132. ИСБН 978-3-642-01481-9.
43. "Магнитные домены в гранулярных материалах GMR". Национальный институт стандартов и технологий. Архивировано из оригинала 12 августа 2011 г. Получено 12 марта 2011 г.
44. Wormington, Matthew; Brown, Elliot (2001). Исследование гигантских магниторезистивных (GMR) спин-клапанных структур с использованием рентгеновской дифракции и отражательной способности (PDF) . Достижения в рентгеновском анализе – труды Денверских рентгеновских конференций. Том 44. Международный центр дифракционных данных. С. 290–294. Архивировано из оригинала (PDF) 5 сентября 2014 г.
45. Dodrill, BC; Kelley, BJ "Magnetic In-line Metrology for GMR Spin-Valve Sensors" (PDF) . Lake Shore Cryotronics. Архивировано из оригинала (PDF) 5 января 2011 г. . Получено 12 марта 2011 г. .
46. Хартманн, У., ред. (2000). Магнитные многослойные структуры и гигантское магнитосопротивление . Серия Springer по поверхностным наукам. Т. 37. Springer. стр. 111. ISBN 978-3-540-65568-8.
47. Третьяк, Львов и Барабанов 2002, стр. 285–286.
48. Третьяк, Львов и Барабанов 2002, стр. 289–291.
49. Зайцев, Д.Д. "Магнетосопротивление, Туннельное". Словарь нанотехнологических терминов и терминов с нанотехнологиями . Роснано. Архивировано из оригинала 23 декабря 2011 года . Проверено 11 апреля 2011 г.

Библиография

• Baibich, MN; Broto, JM; Fert, A.; Nguyen Van Dau, F.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. (1988). "Гигантское магнитосопротивление магнитных сверхрешеток (001)Fe/(001)Cr". Physical Review Letters . 61 (21): 2472–2475. Bibcode :1988PhRvL..61.2472B. doi : 10.1103/PhysRevLett.61.2472 . hdl : 10183/99075 . PMID  10039127.
• Бушоу, КХДж (2005). Краткая энциклопедия магнитных и сверхпроводящих материалов (2-е изд.). Elsevier. ISBN 978-008044586-1.
• Рейг, Кандид; Кардосо, Сусана; Мукхопадхай, Субхас Чандра (2013). Датчики гигантского магниторезистивного (GMR) излучения — от основ до современных приложений. Springer. doi : 10.1007/978-3-642-37172-1. ISBN 978-3-642-37171-4.
• Синдзё, Теруя (29 июня 2009 г.). Наномагнетизм и спинтроника. Elsevier. ISBN 978-008093216-3.
• Третьяк О.В.; Львов, В.А.; Барабанов, О.В. (2002). Физические основы спиновой электроники[ Физические основы спиновой электроники ] (на украинском языке). Киевский университет . ISBN 966-594-323-5.
• Tsymbal, EY; Pettifor, DG (2001). "Перспективы гигантского магнитосопротивления". В Spaepen, Frans; Seitz, Frederick; Turnbull, David; Ehrenreich, Henry (ред.). Физика твердого тела . Физика твердого тела: достижения в исследованиях и приложениях. Том 56. Academic Press. ISBN 978-012607756-8.

Внешние ссылки

• Гигантское магнитосопротивление: действительно большая идея, лежащая в основе очень маленького инструмента Национальная лаборатория сильных магнитных полей
• Презентация GMR-техники (IBM Research) Архивировано 11 января 2012 г. на Wayback Machine