Межфазное тепловое сопротивление

Интерфейсное тепловое сопротивление , также известное как тепловое граничное сопротивление , или сопротивление Капицы , является мерой сопротивления тепловому потоку на границе раздела между двумя материалами. Хотя эти термины могут использоваться взаимозаменяемо, сопротивление Капицы технически относится к атомарно совершенному плоскому интерфейсу, тогда как тепловое граничное сопротивление является более широким термином. ^[1] Это тепловое сопротивление отличается от контактного сопротивления (не путать с электрическим контактным сопротивлением ), поскольку оно существует даже на атомарно совершенных интерфейсах. Из-за различий в электронных и вибрационных свойствах в разных материалах, когда носитель энергии (фонон или электрон, в зависимости от материала) пытается пересечь интерфейс, он будет рассеиваться на интерфейсе. Вероятность передачи после рассеяния будет зависеть от доступных энергетических состояний на стороне 1 и стороне 2 интерфейса.

Предполагая, что постоянный тепловой поток приложен к интерфейсу, это интерфейсное тепловое сопротивление приведет к конечному разрыву температуры на интерфейсе. Из расширения закона Фурье мы можем записать

${\displaystyle Q={\frac {\Delta T}{R}}=G\Delta T}$

где — приложенный поток, — наблюдаемое падение температуры, — тепловое граничное сопротивление, — его обратная величина или тепловая граничная проводимость. ${\displaystyle Q}$ ${\displaystyle \Delta T}$ ${\displaystyle R}$ ${\displaystyle G}$

Понимание термического сопротивления на границе раздела двух материалов имеет первостепенное значение при изучении их термических свойств. Интерфейсы часто вносят значительный вклад в наблюдаемые свойства материалов. Это еще более критично для наномасштабных систем, где интерфейсы могут существенно влиять на свойства относительно объемных материалов.

Низкое тепловое сопротивление на интерфейсах технологически важно для приложений, где необходимо очень высокое рассеивание тепла. Это вызывает особую озабоченность при разработке микроэлектронных полупроводниковых приборов, как определено в Международной технологической дорожной карте для полупроводников 2004 года, где устройство с размером элемента 8 нм, как прогнозируется, будет генерировать до 100000 Вт/см2 ^и потребует эффективного рассеивания тепла ожидаемого теплового потока на уровне кристалла в 1000 Вт/см2, ^что на порядок выше, чем у существующих устройств. ^[2] С другой стороны, приложения, требующие хорошей теплоизоляции, такие как турбины реактивных двигателей, выиграют от интерфейсов с высоким тепловым сопротивлением. Это также потребует интерфейсов материалов, которые стабильны при очень высокой температуре. Примерами являются металлокерамические композиты, которые в настоящее время используются для этих приложений. Высокое тепловое сопротивление также может быть достигнуто с помощью многослойных систем.

Как указано выше, тепловое граничное сопротивление обусловлено рассеянием носителей на интерфейсе. Тип рассеиваемых носителей будет зависеть от материалов, управляющих интерфейсами. Например, на интерфейсе металл-металл эффекты рассеяния электронов будут доминировать над тепловым граничным сопротивлением, поскольку электроны являются основными носителями тепловой энергии в металлах.

Две широко используемые предсказательные модели — это модель акустического несоответствия (AMM) и модель диффузного несоответствия (DMM). AMM предполагает геометрически идеальный интерфейс и перенос фононов через него полностью упругий, рассматривая фононы как волны в континууме. С другой стороны, DMM предполагает, что рассеяние на интерфейсе является диффузным, что верно для интерфейсов с характерной шероховатостью при повышенных температурах.

Моделирование молекулярной динамики (МД) является мощным инструментом для исследования межфазного термического сопротивления. Недавние исследования МД продемонстрировали, что межфазное термическое сопротивление твердое тело-жидкость снижается на наноструктурированных твердых поверхностях за счет увеличения энергии взаимодействия твердое тело-жидкость на единицу площади и уменьшения разницы в вибрационной плотности состояний между твердым телом и жидкостью. ^[3]

Теоретические модели

Основной моделью, которая исторически описывала сопротивление Капицы, является модель фононного газа. ^{[4] [5] [6]} В рамках этой модели существуют модели акустического несоответствия и диффузного несоответствия (AMM и DMM соответственно). Для обеих моделей предполагается, что интерфейс ведет себя точно так же, как и основная масса по обе стороны интерфейса (например, дисперсии объемных фононов, скорости и т. д.), при этом гибридные колебательные моды и фононы, которые их занимают, полностью игнорируются. Кроме того, модели AMM и DMM основаны только на упругом переносе фононов, обычно игнорируя электрические вклады, хотя в модели фононного газа можно учитывать электронные вклады. ^[7] Модели AMM и DMM следует применять для интерфейсов, где по крайней мере один из материалов является электроизолирующим. Тепловое сопротивление тогда является результатом переноса фононов через интерфейс. Энергия передается, когда фононы с более высокой энергией, которые существуют в более высокой плотности в более горячем материале, распространяются в более холодный материал, который, в свою очередь, передает фононы с более низкой энергией, создавая чистый поток энергии . ^[8]

Согласно моделям AMM и DMM, решающим фактором в определении теплового сопротивления на границе раздела является перекрытие фононных состояний. В частности, модели полностью игнорируют эффекты неупругого рассеяния и множественных фононных взаимодействий. Например, модели допускают только взаимодействие фонона, занимающего определенную частоту моды, с другим фононом, занимающим моду точно такой же частоты. В действительности, однако, это не так, и вероятность взаимодействия двух фононов можно рассчитать с помощью теории возмущений (квантовой механики) . В качестве примера в моделях AMM и DMM, учитывая два материала A и B, если материал A имеет низкую популяцию (или отсутствие популяции) фононов с определенным значением k, будет очень мало фононов этого волнового вектора (или, что эквивалентно, частоты) для распространения от A к B. Аналогично, из-за принципа детального баланса , AMM и DMM предсказывают, что очень мало фононов этого волнового вектора будут распространяться в противоположном направлении, от B к A, даже если материал B имеет большую популяцию фононов с этим волновым вектором. Таким образом, поскольку перекрытие между дисперсиями фононов мало, существует меньше мод, позволяющих переносить тепло в материале, что дает высокое тепловое сопротивление интерфейса по сравнению с материалами с высокой степенью перекрытия. ^[9] Ни одна из моделей не является очень эффективной для прогнозирования теплового сопротивления интерфейса (за исключением очень низкой температуры), но для большинства материалов они действуют как верхний и нижний пределы для реального поведения.

AMM и DMM различаются условиями, которые им требуются для распространения через интерфейс, поскольку модели сильно различаются в своей трактовке рассеяния на интерфейсе. В AMM интерфейс предполагается идеальным, что приводит к отсутствию рассеяния, поэтому фононы распространяются упруго через интерфейс. Волновые векторы, которые распространяются через интерфейс, определяются сохранением импульса. В DMM предполагается противоположная крайность — идеально рассеивающий интерфейс. В этом случае волновые векторы, которые распространяются через интерфейс, случайны и не зависят от падающих фононов на интерфейс. Для обеих моделей по-прежнему должен соблюдаться детальный баланс.

Для обеих моделей применимы основные уравнения модели фононного газа. ^{[4] [5] [6]} Поток энергии из одного материала в другой в одном измерении равен:

${\displaystyle Q_{1,2}=\sum _{k}n\left(k,T_{1}\right)E\nu \alpha \left(k,T_{1},T_{2}\right)}$

где — групповая скорость , которая аппроксимируется как скорость звука в материале для моделей AMM и DMM, — число фононов при заданном волновом векторе, E — энергия, а α — вероятность передачи через интерфейс. Таким образом, чистый поток — это разность потоков энергии: ${\displaystyle \nu }$ ${\displaystyle n\left(k,T_{1}\right)}$

${\displaystyle Q_{net}\ =\ Q_{1,2}\ -\ Q_{2,1}}$

Поскольку оба потока зависят от T ₁ и T ₂ , соотношение между потоком и разницей температур можно использовать для определения сопротивления теплового интерфейса на основе:

${\displaystyle R_{th}\ =\ {\frac {\Delta T}{Q/A}}}$

где A — площадь интерфейса. Эти основные уравнения составляют основу обеих моделей. n определяется на основе дисперсионного соотношения для материалов (например, модели Дебая ) и статистики Бозе-Эйнштейна . Энергия просто задается уравнением длины волны Де Бройля :

${\displaystyle E\ =\ \hbar \ \omega \left(k\right)\ }$

где . Основное различие между двумя моделями заключается в вероятности передачи , определение которой является более сложным. В каждом случае она определяется основными предположениями, которые формируют соответствующие модели. Предположение об упругом рассеянии затрудняет передачу фононов через интерфейс, что приводит к более низким вероятностям. В результате модель акустического несоответствия обычно представляет верхний предел для сопротивления теплового интерфейса, в то время как модель диффузного несоответствия представляет нижний предел. ^[10]

Примеры

Интерфейсы жидкого гелия

Типичное сопротивление интерфейса жидкого гелия с металлами. Сопротивление умножено на T ³ для устранения ожидаемой зависимости T ⁻³ . Адаптировано из ^[9]

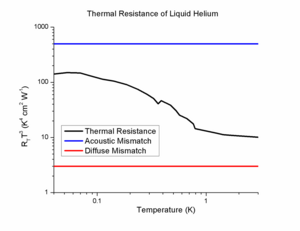
Наличие сопротивления теплового интерфейса, соответствующего прерывистой температуре на интерфейсе, было впервые предложено в исследованиях жидкого гелия в 1936 году. Хотя эта идея была впервые предложена в 1936 году, ^[9] только в 1941 году Петр Капица (Peter Kapitza) провел первое систематическое исследование поведения теплового интерфейса в жидком гелии. ^[11] Первой крупной моделью теплопередачи на интерфейсах была модель акустического несоответствия, которая предсказывала зависимость температуры T ⁻³ от сопротивления интерфейса, но она не смогла правильно смоделировать теплопроводность интерфейсов гелия на целых два порядка величины. Другое удивительное поведение теплового сопротивления наблюдалось в зависимости от давления . Поскольку скорость звука является сильной функцией температуры в жидком гелии, модель акустического несоответствия предсказывает сильную зависимость сопротивления интерфейса от давления. Исследования около 1960 года неожиданно показали, что сопротивление интерфейса почти не зависело от давления, что предполагает, что доминируют другие механизмы.

Теория акустического несоответствия предсказывала очень высокое тепловое сопротивление (низкую теплопроводность) на интерфейсах твердое тело-гелий. Это проблематично для исследователей, работающих при сверхнизких температурах, поскольку это значительно затрудняет скорость охлаждения при низких температурах, таких как в холодильниках растворения. ^[12] К счастью, такое большое тепловое сопротивление не наблюдалось из-за многих механизмов, которые способствовали переносу фононов. В жидком гелии силы Ван-дер-Ваальса фактически работают на затвердевание первых нескольких монослоев на твердом теле. Этот пограничный слой функционирует во многом как антибликовое покрытие в оптике, так что фононы, которые обычно отражаются от интерфейса, на самом деле проходят через интерфейс. Это также помогает понять независимость теплопроводности от давления. Последним доминирующим механизмом аномально низкого теплового сопротивления интерфейсов жидкого гелия является эффект шероховатости поверхности , который не учитывается в модели акустического несоответствия. Более подробную теоретическую модель этого аспекта см. в статье А. Хатера и Дж. Шефтеля. ^[13] Подобно электромагнитным волнам , которые создают поверхностные плазмоны на шероховатых поверхностях, фононы также могут вызывать поверхностные волны. Когда эти волны в конечном итоге рассеиваются, они обеспечивают другой механизм для передачи тепла через интерфейс. Аналогично фононы также способны создавать затухающие волны в геометрии полного внутреннего отражения . В результате, когда эти волны рассеиваются в твердом теле, дополнительное тепло передается от гелия за пределы предсказания теории акустического несоответствия. Для более полного обзора по этой теме см. обзор Шварца. ^[14]

Значительная теплопроводность при комнатной температуре

В целом, в материалах есть два типа теплоносителей: фононы и электроны. Свободный электронный газ, содержащийся в металлах, является очень хорошим проводником тепла и доминирует в теплопроводности . Однако все материалы демонстрируют перенос тепла посредством переноса фононов, поэтому тепло течет даже в диэлектрических материалах, таких как кремний. Теплопроводность на границе раздела является мерой того, насколько эффективно теплоносители перетекают из одного материала в другой. На сегодняшний день самым низким измерением теплопроводности при комнатной температуре является алмаз с концевыми группами Bi/Hydrogen с теплопроводностью 8,5 МВт м ⁻² K ⁻¹ . Как металл, висмут содержит много электронов, которые служат основными теплоносителями. С другой стороны, алмаз является очень хорошим электроизолятором (хотя он имеет очень высокую теплопроводность), поэтому перенос электронов между материалами равен нулю. Кроме того, эти материалы имеют очень разные параметры решетки, поэтому фононы неэффективно связываются через интерфейс. Наконец, температура Дебая между материалами значительно различается. В результате висмут, имеющий низкую температуру Дебая, имеет много фононов на низких частотах. Алмаз, с другой стороны, имеет очень высокую температуру Дебая, и большинство его теплопереносящих фононов находятся на частотах, намного более высоких, чем те, которые присутствуют в висмуте. ^[15]

Данные по теплопроводности адаптированы из ^{[14] [15] [16]}

Увеличивая теплопроводность, большинство интерфейсов с фононным опосредованием (диэлектрик-диэлектрик и металл-диэлектрик) имеют теплопроводность от 80 до 300 МВт м ⁻² К ⁻¹ . Наибольшая теплопроводность с фононным опосредованием, измеренная на сегодняшний день, была между TiN (нитрид титана) и MgO . Эти системы имеют очень похожие структуры решетки и температуры Дебая. Хотя нет свободных электронов для повышения теплопроводности интерфейса, схожие физические свойства двух кристаллов способствуют очень эффективной передаче фононов между двумя материалами. ^[11]

На самом высоком конце спектра одна из самых высоких теплопроводностей измерена между алюминием и медью . При комнатной температуре интерфейс Al-Cu имеет проводимость 4 ГВт м ⁻² К ⁻¹ . Высокая теплопроводность интерфейса не должна быть неожиданной, учитывая высокую электропроводность обоих материалов. ^[16]

Межфазное сопротивление в углеродных нанотрубках

Превосходная теплопроводность углеродных нанотрубок делает их отличным кандидатом для создания композитных материалов. Но межфазное сопротивление влияет на эффективную теплопроводность. Эта область недостаточно изучена, и было проведено лишь несколько исследований, чтобы понять основной механизм этого сопротивления. ^{[17] [18]}

Ссылки

1. Гири, А.; Хопкинс, П.Е. (2020). «Обзор экспериментальных и вычислительных достижений в области тепловой граничной проводимости и наномасштабного теплового транспорта через твердые интерфейсы». Advanced Functional Materials . 30 (8): 1903857. doi :10.1002/adfm.201903857. S2CID  202037103.
2. Ху, Мин; Кеблински, Павел; Ван, Цзянь-Шэн; Раравикар, Начикет (2008). «Интерфейсная теплопроводность между кремнием и вертикальной углеродной нанотрубкой». Журнал прикладной физики . 104 (8): 083503–083503–4. Bibcode : 2008JAP...104h3503H. doi : 10.1063/1.3000441.
3. Ху, Хан; Сан, Ин (2012). «Влияние наноструктур на сопротивление Капицы на границе раздела вода-золото во время кипения: исследование молекулярной динамики». Журнал прикладной физики . 112 (5). Издательство AIP: 053508–053508–6. Bibcode : 2012JAP...112e3508H. doi : 10.1063/1.4749393.
4. Стэнли, Кристофер М. (май 2018 г.). Тепловой поток и сопротивление Капицы через интерфейс Si|SiO2: исследование первых принципов (диссертация). hdl : 2346/73843 . OCLC  1045421642.
5. Gordiz, Kiarash; Henry, Asegun (16 марта 2016 г.). "Фононный транспорт на кристаллических интерфейсах Si/Ge: роль интерфейсных мод вибрации". Scientific Reports . 6 (1): 23139. Bibcode :2016NatSR...623139G. doi : 10.1038/srep23139 . PMC 4793224 . PMID  26979787. S2CID  8893499. 
6. Stanley, Christopher M.; Rader, Benjamin K.; Laster, Braxton HD; Servati, Mahsa; Estreicher, Stefan K. (декабрь 2021 г.). «Роль интерфейсных колебательных мод в тепловом граничном сопротивлении». Physica Status Solidi A. 218 ( 23): 2100111. Bibcode : 2021PSSAR.21800111S. doi : 10.1002/pssa.202100111. S2CID  236408006.
7. Моначон, Кристиан; Вебер, Людгер; Деймс, Крис (1 июля 2016 г.). «Тепловая граничная проводимость: перспектива материаловедения». Annual Review of Materials Research . 46 (1): 433–463. Bibcode : 2016AnRMS..46..433M. doi : 10.1146/annurev-matsci-070115-031719 .
8. Swartz, Eric Thomas (1987). Тепловое сопротивление границы твердого тела (диссертация). Bibcode :1987PhDT.......170S. ProQuest  303581612.
9. Swartz, ET; Pohl, RO (1 июля 1989). "Тепловое граничное сопротивление". Reviews of Modern Physics . 61 (3): 605–668. Bibcode :1989RvMP...61..605S. doi :10.1103/revmodphys.61.605.
10. Цзэн, Таофан; Чэнь, Ган (1 апреля 2001 г.). «Фононная теплопроводность в тонких пленках: влияние теплового граничного сопротивления и внутреннего тепловыделения». Журнал теплопередачи . 123 (2): 340–347. doi :10.1115/1.1351169.
11. Kapitza, PL (15 августа 1941 г.). «Теплопередача и сверхтекучесть гелия II». Physical Review . 60 (4): 354–355. Bibcode :1941PhRv...60..354K. doi :10.1103/PhysRev.60.354.
12. – обзор». Криогеника . 121. doi : 10.1016/j.cryogenics.2021.103390 . S2CID  244005391.
13. Хатер, А.; Шефтель, Дж. (1987-05-01). «Теория сопротивления Капицы». Physical Review B. 35 ( 13). Американское физическое общество (APS): 6749–6755. Bibcode : 1987PhRvB..35.6749K. doi : 10.1103/physrevb.35.6749. PMID  9940924.
14. Lyeo, Ho-Ki; Cahill, David G. (2006-04-03). "Теплопроводность интерфейсов между сильно разнородными материалами". Physical Review B. 73 ( 14). Американское физическое общество (APS): 144301. Bibcode : 2006PhRvB..73n4301L. doi : 10.1103/physrevb.73.144301.
15. Costescu, Ruxandra M.; Wall, Marcel A.; Cahill, David G. (2003-02-27). "Теплопроводность эпитаксиальных интерфейсов". Physical Review B. 67 ( 5). Американское физическое общество (APS): 054302. Bibcode : 2003PhRvB..67e4302C. doi : 10.1103/physrevb.67.054302.
16. Gundrum, Bryan C.; Cahill, David G.; Averback, Robert S. (2005-12-30). "Теплопроводность интерфейсов металл-металл". Physical Review B. 72 ( 24). Американское физическое общество (APS): 245426. Bibcode : 2005PhRvB..72x5426G. doi : 10.1103/physrevb.72.245426.
17. Чжун, Хунлян; Люкс, Дженнифер Р. (2006-09-01). "Интерфейсное тепловое сопротивление между углеродными нанотрубками: моделирование молекулярной динамики и аналитическое тепловое моделирование". Physical Review B. 74 ( 12). Американское физическое общество (APS): 125403. Bibcode : 2006PhRvB..74l5403Z. doi : 10.1103/physrevb.74.125403.
18. Эстрада, Дэвид; Поп, Эрик (2011-02-14). "Визуализация рассеивания и горячие точки в транзисторах с углеродными нанотрубками". Applied Physics Letters . 98 (7). AIP Publishing: 073102. arXiv : 1011.4551 . Bibcode : 2011ApPhL..98g3102E. doi : 10.1063/1.3549297. S2CID  40975236.