Правило Литтлвуда–Ричардсона

В математике правило Литтлвуда –Ричардсона представляет собой комбинаторное описание коэффициентов, возникающих при разложении произведения двух функций Шура в линейную комбинацию других функций Шура. Эти коэффициенты являются натуральными числами, которые правило Литтлвуда–Ричардсона описывает как подсчет определенных перекошенных таблиц . Они встречаются во многих других математических контекстах, например, как кратность в разложении тензорных произведений конечномерных представлений общих линейных групп или в разложении определенных индуцированных представлений в теории представлений симметрической группы или в области алгебраической комбинаторики, имеющей дело с таблицами Юнга и симметрическими многочленами .

Коэффициенты Литтлвуда–Ричардсона зависят от трех разбиений , скажем , из которых и описывают функции Шура, которые умножаются, и дают функцию Шура, коэффициентом в линейной комбинации которой является этот; другими словами, это коэффициенты, такие что ${\displaystyle \lambda ,\mu ,\nu }$ ${\displaystyle \lambda }$ ${\displaystyle \mu }$ ${\displaystyle \nu }$ ${\displaystyle c_{\lambda ,\mu }^{\nu }}$

${\displaystyle s_{\lambda }s_{\mu }=\sum _{\nu }c_{\lambda ,\mu }^{\nu }s_{\nu }.}$

Правило Литтлвуда–Ричардсона гласит, что равно числу таблиц Литтлвуда–Ричардсона косой формы и веса . ${\displaystyle c_{\lambda ,\mu }^{\nu }}$ ${\displaystyle \nu /\lambda }$ ${\displaystyle \mu }$

История

К сожалению, правило Литтлвуда–Ричардсона доказать гораздо сложнее, чем предполагалось изначально. Автору когда-то сказали, что правило Литтлвуда–Ричардсона помогло отправить людей на Луну, но не было доказано до тех пор, пока они там не оказались.

Гордон Джеймс (1987)

Правило Литтлвуда–Ричардсона впервые было сформулировано DE Littlewood и AR Richardson  (1934, теорема III, стр. 119), но хотя они и утверждали его как теорему, они доказали его только в некоторых довольно простых частных случаях. Робинсон  (1938) утверждал, что завершил их доказательство, но его аргумент имел пробелы, хотя он был настолько неясно написан, что эти пробелы не были замечены в течение некоторого времени, и его аргумент воспроизведен в книге (Littlewood 1950). Некоторые из пробелов были позже заполнены Macdonald (1995). Первые строгие доказательства правила были даны через четыре десятилетия после того, как оно было обнаружено, Schützenberger (1977) и Thomas (1974), после того, как необходимая комбинаторная теория была разработана C. Schensted  (1961), Schützenberger (1963) и Knuth  (1970) в их работе о соответствии Robinson–Schensted . В настоящее время существует несколько коротких доказательств правила, например (Gasharov 1998) и (Stembridge 2002) с использованием инволюций Бендера-Кнута . Литтельманн (1994) использовал модель путей Литтельмана для обобщения правила Литтлвуда-Ричардсона на другие полупростые группы Ли.

Правило Литтлвуда–Ричардсона печально известно количеством ошибок, которые появились до его полного опубликованного доказательства. Несколько опубликованных попыток доказать его неполны, и особенно трудно избежать ошибок при ручных вычислениях с ним: даже оригинальный пример в DE Littlewood и AR Richardson (1934) содержит ошибку.

Таблицы Литтлвуда–Ричардсона

Картина Литтлвуда–Ричардсона

Таблица Литтлвуда–Ричардсона — это перекошенная полустандартная таблица с дополнительным свойством, что последовательность, полученная путем конкатенации ее перевернутых строк, является решетчатым словом (или решетчатой ​​перестановкой), что означает, что в каждой начальной части последовательности любое число встречается по крайней мере так же часто, как число . Другая эквивалентная (хотя и не совсем очевидная) характеристика состоит в том, что сама таблица и любая таблица, полученная из нее путем удаления некоторого числа ее самых левых столбцов, имеют слабо убывающий вес. Было найдено много других комбинаторных понятий, которые оказываются биекцией с таблицами Литтлвуда–Ричардсона и, следовательно, также могут использоваться для определения коэффициентов Литтлвуда–Ричардсона. ${\displaystyle i}$ ${\displaystyle i+1}$

Еще одна картина Литтлвуда–Ричардсона

Пример

Рассмотрим случай, когда , и . Тогда тот факт, что можно вывести из того факта, что две таблицы, показанные справа, являются единственными двумя таблицами Литтлвуда–Ричардсона с формой и весом . Действительно, поскольку последний ящик на первой непустой строке косой диаграммы может содержать только запись 1, вся первая строка должна быть заполнена записями 1 (это верно для любой таблицы Литтлвуда–Ричардсона); в последнем ящике второй строки мы можем разместить только 2 по строгости столбца и тот факт, что наше решетчатое слово не может содержать никакой большей записи, прежде чем оно будет содержать 2. Для первого ящика второй строки мы теперь можем использовать либо 1, либо 2. Как только эта запись выбрана, третья строка должна содержать оставшиеся записи, чтобы сделать вес (3,2,1) в слабо возрастающем порядке, поэтому у нас больше не остается выбора; в обоих случаях оказывается, что мы находим таблицу Литтлвуда–Ричардсона. ${\displaystyle \lambda =(2,1)}$ ${\displaystyle \mu =(3,2,1)}$ ${\displaystyle \nu =(4,3,2)}$ ${\displaystyle c_{\lambda ,\mu }^{\nu }=2}$ ${\displaystyle \nu /\lambda }$ ${\displaystyle \mu }$

Более геометрическое описание

Условие, что последовательность записей, считываемых из таблицы в несколько своеобразном порядке, образует решетчатое слово, можно заменить более локальным и геометрическим условием. Поскольку в полустандартной таблице одинаковые записи никогда не встречаются в одном и том же столбце, можно пронумеровать копии любого значения справа налево, что является порядком их появления в последовательности, которая должна быть решетчатым словом. Назовем число, таким образом связанное с каждой записью, ее индексом и запишем запись i с индексом j как i [ j ]. Теперь, если некоторая таблица Литтлвуда–Ричардсона содержит запись с индексом j , то эта запись i [ j ] должна встречаться в строке строго ниже, чем (что, безусловно, также происходит, поскольку запись i  − 1 встречается не реже, чем запись i ). Фактически запись i [ j ] должна также встречаться в столбце не правее этой самой записи (что на первый взгляд кажется более строгим условием). Если вес таблицы Литтлвуда–Ричардсона зафиксирован заранее, то можно сформировать фиксированную коллекцию индексированных записей, и если они размещены таким образом, чтобы соблюдались эти геометрические ограничения, в дополнение к ограничениям полустандартных таблиц и условию, что индексированные копии тех же записей должны соблюдать порядок индексов справа налево, то полученные таблицы гарантированно будут таблицами Литтлвуда–Ричардсона. ${\displaystyle i>1}$ ${\displaystyle (i-1)[j]}$ ${\displaystyle (i-1)[j]}$

Алгоритмическая форма правила

Указанный выше Литтлвуд–Ричардсон дает комбинаторное выражение для отдельных коэффициентов Литтлвуда–Ричардсона, но не дает никаких указаний на практический метод перечисления таблиц Литтлвуда–Ричардсона для нахождения значений этих коэффициентов. Действительно, для заданных нет простого критерия для определения того, существуют ли вообще какие-либо таблицы Литтлвуда–Ричардсона формы и веса (хотя есть ряд необходимых условий, простейшим из которых является ); поэтому кажется неизбежным, что в некоторых случаях приходится проводить сложный поиск, только чтобы обнаружить, что никаких решений не существует. ${\displaystyle \lambda ,\mu ,\nu }$ ${\displaystyle \nu /\lambda }$ ${\displaystyle \mu }$ ${\displaystyle |\lambda |+|\mu |=|\nu |}$

Тем не менее, правило приводит к довольно эффективной процедуре определения полного разложения произведения функций Шура, другими словами, к определению всех коэффициентов для фиксированных λ и μ, но изменяющегося ν. Это фиксирует вес таблиц Литтлвуда–Ричардсона, которые должны быть построены, и «внутреннюю часть» λ их формы, но оставляет «внешнюю часть» ν свободной. Поскольку вес известен, набор индексированных записей в геометрическом описании фиксирован. Теперь для последовательных индексированных записей все возможные позиции, разрешенные геометрическими ограничениями, могут быть перебраны в поиске с возвратом . Записи могут быть перебраны в порядке возрастания, в то время как среди равных записей они могут быть перебраны по убыванию индекса. Последний момент является ключом к эффективности процедуры поиска: запись i [ j ] тогда ограничивается тем, чтобы находиться в столбце справа от , но не правее (если такие записи присутствуют). Это сильно ограничивает набор возможных позиций, но всегда оставляет по крайней мере одну допустимую позицию для ; Таким образом, каждое размещение записи приведет к возникновению по крайней мере одной полной таблицы Литтлвуда–Ричардсона, а дерево поиска не будет содержать тупиков. ${\displaystyle c_{\lambda ,\mu }^{\nu }}$ ${\displaystyle i[j+1]}$ ${\displaystyle i-1[j]}$ ${\displaystyle i[j]}$

Аналогичный метод можно использовать для нахождения всех коэффициентов при фиксированных λ и ν, но изменяющемся μ. ${\displaystyle c_{\lambda ,\mu }^{\nu }}$

Коэффициенты Литтлвуда–Ричардсона

Коэффициенты Литтлвуда–Ричардсона c^ν
_λμ   проявляются следующими взаимосвязанными способами:

• Они являются структурными константами для произведения в кольце симметричных функций относительно базиса функций Шура

${\displaystyle s_{\lambda }s_{\mu }=\sum c_{\lambda \mu }^{\nu }s_{\nu }}$

или эквивалентно c^ν
_λμ   является внутренним произведением s _ν и s _λ s _μ .

• Они выражают косые функции Шура через функции Шура

${\displaystyle s_{\nu /\lambda }=\sum _{\mu }c_{\lambda \mu }^{\nu }s_{\mu }.}$

• С​^ν
  _λμ   появляются как числа пересечения на грассманиане :

${\displaystyle \sigma _{\lambda }\sigma _{\mu }=\sum c_{\lambda \mu }^{\nu }\sigma _{\nu }}$

где σ _μ — класс многообразия Шуберта грассманиана, соответствующего  μ .

• с^ν
  _λμ   — это число раз, когда неприводимое представление V _λ ⊗ V _μ произведения симметрических групп S _{| λ |} × S _{| μ |} встречается в ограничении представления V _ν группы S _{| ν |} на S _{| λ |} × S _{| μ |} . По принципу взаимности Фробениуса это также число раз, когда V _ν встречается в представлении S _{| ν |,} индуцированном из V _λ  ⊗  V _μ .
• С​^ν
  _λμ   появляются в разложении тензорного произведения (Fulton 1997) двух модулей Шура (неприводимые представления специальных линейных групп)

${\displaystyle E^{\lambda }\otimes E^{\mu }=\bigoplus _{\nu }(E^{\nu })^{\oplus c_{\lambda \mu }^{\nu }}.}$

• с^ν
  _λμ   — это число стандартных таблиц Юнга формы ν / μ , которые в игровой форме эквивалентны некоторой фиксированной стандартной таблице Юнга формы  λ .
• с^ν
  _λμ   — число таблиц Литтлвуда–Ричардсона формы ν / λ и веса  μ .
• с^ν
  _λμ   — это количество изображений между μ и ν/λ.

Особые случаи

Формула Пьери

Формула Пьери , которая является частным случаем правила Литтлвуда–Ричардсона в случае, когда одно из разбиений имеет только одну часть , утверждает, что

${\displaystyle S_{\mu }S_{n}=\sum _{\lambda }S_{\lambda }}$

где S _n — функция Шура разбиения с одной строкой, а сумма берется по всем разбиениям λ, полученным из μ путем добавления n элементов к его диаграмме Феррерса , причем никакие два элемента не находятся в одном столбце.

Прямоугольные перегородки

Если оба раздела имеют прямоугольную форму, сумма также не имеет кратности (Okada 1998). Зафиксируем a , b , p и q положительные целые числа с p q . Обозначим через раздел с p частями длины a . Разделы, индексирующие нетривиальные компоненты, — это разделы с длиной, такой что ${\displaystyle \geq }$ ${\displaystyle (a^{p})}$ ${\displaystyle s_{(a^{p})}s_{(b^{q})}}$ ${\displaystyle \lambda }$ ${\displaystyle \leq p+q}$

• ${\displaystyle \lambda _{q+1}=\lambda _{q+2}=\cdots =\lambda _{p}=a,}$
• ${\displaystyle \lambda _{q}\geq \mathrm {max} (a,b)}$
• ${\displaystyle \lambda _{i}+\lambda _{p+q-i+1}=a+b,\quad {i=1,\dots ,q}.}$

Например,

.

Обобщения

Приведенные коэффициенты Кронекера симметрической группы

Приведенный коэффициент Кронекера симметрической группы является обобщением на три произвольные диаграммы Юнга , которая симметрична относительно перестановок трех диаграмм. ${\displaystyle {\bar {C}}_{\lambda ,\mu ,\nu }}$ ${\displaystyle c_{\lambda ,\mu }^{\nu }}$ ${\displaystyle \lambda ,\mu ,\nu }$

Косые функции Шура

Зелевинский (1981) расширил правило Литтлвуда–Ричардсона для искажения функций Шура следующим образом:

${\displaystyle s_{\lambda }s_{\mu /\nu }=\sum _{\lambda +\omega (T_{\geq j})\in P}s_{\lambda +\omega (T)}}$

где сумма берется по всем таблицам T на μ/ν таким образом, что для всех j последовательность целых чисел λ+ω( T _{≥ j} ) не возрастает, а ω — вес.

Числа Ньюэлла-Литтлвуда

Числа Ньюэлла-Литтлвуда определяются через коэффициенты Литтлвуда-Ричардсона с помощью кубического выражения ^[1]

${\displaystyle N_{\mu ,\nu ,\lambda }=\sum _{\alpha ,\beta ,\gamma }c_{\alpha ,\beta }^{\mu }c_{\alpha ,\gamma }^{\nu }c_{\beta ,\gamma }^{\lambda }}$

Числа Ньюэлла-Литтлвуда дают некоторые кратности тензорного произведения конечномерных представлений классических групп Ли типов . ${\displaystyle B,C,D}$

Условие неисчезания размеров диаграммы Юнга приводит к ${\displaystyle c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |}$

${\displaystyle N_{\mu ,\nu ,\lambda }\neq 0\implies \left\{{\begin{array}{l}||\lambda |-|\mu ||\leq |\nu |\leq |\lambda |+|\mu |\\|\lambda |+|\mu |+|\nu |\in 2\mathbb {Z} \end{array}}\right.}$

Числа Ньюэлла-Литтлвуда являются обобщениями коэффициентов Литтлвуда-Ричардсона в том смысле, что

${\displaystyle |\mu |+|\nu |=|\lambda |\implies N_{\mu ,\nu ,\lambda }=c_{\mu ,\nu }^{\lambda }}$

Числа Ньюэлла-Литтлвуда, включающие диаграмму Юнга только с одной строкой, подчиняются правилу типа Пьери: — это число способов удалить ящики из (из разных столбцов), а затем добавить ящики (в разные столбцы), чтобы получить . ^[1] ${\displaystyle N_{(k),\mu ,\nu }}$ ${\displaystyle {\frac {k+|\mu |-|\nu |}{2}}}$ ${\displaystyle \mu }$ ${\displaystyle {\frac {k-|\mu |+|\nu |}{2}}}$ ${\displaystyle \nu }$

Числа Ньюэлла-Литтлвуда являются структурными константами ассоциативной и коммутативной алгебры, базисными элементами которой являются разбиения, с произведением . Например, ${\displaystyle \mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda }$

${\displaystyle (1)\times (k)=(k-1)+(k+1)+(k,1)\quad {\text{(Newell–Littlewood)}}}$

${\displaystyle (1)\times (k)=(k+1)+(k,1)\quad {\text{(Littlewood–Richardson)}}}$

Примеры

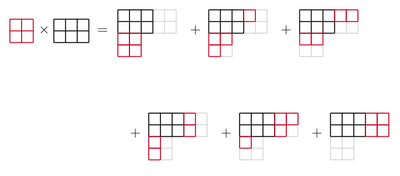
Примеры коэффициентов Литтлвуда–Ричардсона ниже даны в терминах произведений полиномов Шура S _π , индексированных разбиениями π , с использованием формулы

${\displaystyle S_{\lambda }S_{\mu }=\sum c_{\lambda \mu }^{\nu }S_{\nu }.}$

Все коэффициенты, не превышающие 4, определяются по формуле: ${\displaystyle |\nu |}$

• S ₀ S _π = S _π для любого π. где S ₀ =1 — полином Шура пустого разбиения
• С ₁ С ₁ = С ₂ + С ₁₁
• С ₂ С ₁ = С ₃ + С ₂₁
• С ₁₁ С ₁ = С ₁₁₁ + С ₂₁
• С ₃ С ₁ = С ₄ + С ₃₁
• С ₂₁ С ₁ = С ₃₁ + С ₂₂ + С ₂₁₁
• С ₂ С ₂ = С ₄ + С ₃₁ + С ₂₂
• С ₂ С ₁₁ = С ₃₁ + С ₂₁₁
• С ₁₁₁ С ₁ = С ₁₁₁₁ + С ₂₁₁
• С ₁₁ С ₁₁ = С ₁₁₁₁ + С ₂₁₁ + С ₂₂

Большинство коэффициентов для малых разбиений равны 0 или 1, что происходит, в частности, всякий раз, когда один из факторов имеет форму S _n или S _11...1 , из-за формулы Пьери и ее транспонированного аналога. Простейший пример с коэффициентом больше 1 происходит, когда ни один из факторов не имеет такой формы:

• С ₂₁ С ₂₁ = С ₄₂ + С ₄₁₁ + С ₃₃ + 2 С ₃₂₁ + С ₃₁₁₁ + С ₂₂₂ + С ₂₂₁₁ .

Для больших разделов коэффициенты становятся сложнее. Например,

• С ₃₂₁ С ₃₂₁ = С ₆₄₂ + С ₆₄₁₁ + С ₆₃₃ +2 С ₆₃₂₁ + С ₆₃₁₁₁ + С ₆₂₂₂ + С ₆₂₂₁₁ + С ₅₅₂ + С ₅₅₁₁ +2 С ₅₄₃ +4 С ₅₄₂₁ +2 С ₅₄₁₁₁ +3 С ₅₃₃₁ +3 С ₅₃₂₂ +4 С ₅₃₂₁₁ + С ₅₃₁₁₁₁ +2 С ₅₂₂₂₁ + С ₅₂₂₁₁₁ + С ₄₄₄ +3 С ₄₄₃₁ +2 С ₄₄₂₂ +3 С ₄₄₂₁₁ + С ₄₄₁₁₁₁ +3 С ₄₃₃₂ +3 С ₄₃₃₁₁ +4 С ₄₃₂₂₁ +2 С ₄₃₂₁₁₁ + С ₄₂₂₂₂ + С ₄₂₂₂₁₁ + S ₃₃₃₃ +2 S ₃₃₃₂₁ + S ₃₃₃₁₁₁ + S ₃₃₂₂₂ + S ₃₃₂₂₁₁ с 34 членами и общей кратностью 62, а наибольший коэффициент равен 4
• S ₄₃₂₁ S ₄₃₂₁ представляет собой сумму 206 членов с общей кратностью 930, а наибольший коэффициент равен 18.
• S ₅₄₃₂₁ S ₅₄₃₂₁ представляет собой сумму 1433 членов с общей кратностью 26704, а наибольший коэффициент (у S _86543211 ) равен 176.
• S ₆₅₄₃₂₁ S ₆₅₄₃₂₁ представляет собой сумму 10873 членов с общей кратностью 1458444 (поэтому среднее значение коэффициентов больше 100, и они могут достигать 2064).

Первоначальный пример, приведенный Литтлвудом и Ричардсоном (1934, стр. 122-124), был следующим (после исправления трех таблиц, которые они нашли, но забыли включить в окончательную сумму):

• С ₄₃₁ С ₂₂₁ = С ₆₅₂ + С ₆₅₁₁ + С ₆₄₃ + 2 С ₆₄₂₁ + С ₆₄₁₁₁ + С _{6331 +} С ₆₃₂₂ + С ₆₃₂₁₁ + С ₅₅₃ + 2 С ₅₅₂₁ + С ₅₅₁₁₁ + 2 С ₅₄₃₁ + 2 С ₅₄₂₂ + 3 С ₅₄₂₁₁ + С ₅₄₁₁₁₁ + С ₅₃₃₂ + С ₅₃₃₁₁ + 2 С ₅₃₂₂₁ + С ₅₃₂₁₁₁ + С ₄₄₃₂ + С ₄₄₃₁₁ + 2 С ₄₄₂₂₁ + С ₄₄₂₁₁₁ + С ₄₃₃₂₁ + С ₄₃₂₂₂ + С ₄₃₂₂₁₁

с 26 терминами, полученными из следующих 34 таблиц:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ...22 ...22 ...2 ...2 ...2 ...2 ... ... ....3 . .23 .2 .3 . .22 .2 .2  3 3 2 2 3 23 2  3 3....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ...12 ...12 ...12 ...12 ...2 ...1 ...1 ...2 ...1.23 .2 .3 . .13 .22 .2 .1 .2  3 2 2 2 3 23 23 2 3 3....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ...2 ...2 ...2 ... ... ... ... ... .1 .3 . .12 .12 .1 .2 .2 2 1 1 23 2 22 13 13 2 2 3 3 2 2 3 3.... .... .... .... .... .... .... .... ...1 ...1 ...1 ...1 ...1 ... ... ... .12 .12 .1 .2 .2 .11 .1 .1 23 2 22 13 1 22 12 12 3 3 2 2 3 23 2 3 3

Вычисление перекошенных функций Шура аналогично. Например, 15 таблиц Литтлвуда–Ричардсона для ν=5432 и λ=331 имеют вид

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 .. .11 ...11 ...11...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 .. .2 ...2 ...2.11 .11 .11 .12 .11 .12 .13 .13 .23 .13 .13 .12 .12 .23 .2312 13 22 12 23 13 12 24 14 14 22 23 33 13 34

поэтому S _5432/331 = Σ c^ν
_λμ  S _μ = S ₅₂ + S ₅₁₁ + S ₄₁₁₁ + S ₂₂₂₁ + 2 S ₄₃ + 2 S ₃₂₁₁ + 2 S ₃₂₂ + 2 S ₃₃₁ + 3 S ₄₂₁ (Фултон 1997, стр. 64).

Примечания

1. Гао, Шилян; Ореловиц, Гидон; Йонг, Александр (2021). «Числа Ньюэлла-Литтлвуда». Trans. Amer. Math. Soc . 374 (9): 6331–6366. arXiv : 2005.09012v1 . doi :10.1090/tran/8375. S2CID  218684561.

Ссылки

• Фултон, Уильям (1997), Таблицы Юнга , Студенческие тексты Лондонского математического общества, т. 35, Cambridge University Press , стр. 121, ISBN 978-0-521-56144-0, г-н  1464693
• Гашаров, Веселин (1998), «Краткое доказательство правила Литтлвуда-Ричардсона», European Journal of Combinatorics , 19 (4): 451–453, doi : 10.1006/eujc.1998.0212 , ISSN  0195-6698, MR  1630540
• Джеймс, Гордон (1987), «Теория представлений симметрических групп», Конференция Arcata по представлениям конечных групп (Arcata, Калифорния, 1986) , Труды симпозиума по чистой математике, т. 47, Провиденс, Род-Айленд: Американское математическое общество , стр. 111–126, MR  0933355
• Кнут, Дональд Э. (1970), «Перестановки, матрицы и обобщенные таблицы Юнга», Pacific Journal of Mathematics , 34 (3): 709–727, doi : 10.2140/pjm.1970.34.709 , ISSN  0030-8730, MR  0272654
• Литтельманн, Питер (1994), «Правило Литтлвуда-Ричардсона для симметризуемых алгебр Каца-Муди» (PDF) , Invent. Math. , 116 : 329–346, Bibcode :1994InMat.116..329L, doi :10.1007/BF01231564, S2CID  85546837
• Литтлвуд, Дадли Э. (1950), Теория групповых характеров и матричных представлений групп, AMS Chelsea Publishing, Провиденс, Род-Айленд, ISBN 978-0-8218-4067-2, МР  0002127
• Littlewood, DE; Richardson, AR (1934), "Групповые характеры и алгебра", Philosophical Transactions of the Royal Society of London. Серия A, содержащая статьи математического или физического характера , 233 (721–730), The Royal Society: 99–141, Bibcode : 1934RSPTA.233...99L, doi : 10.1098/rsta.1934.0015 , ISSN  0264-3952, JSTOR  91293
• Макдональд, И. Г. (1995), Симметричные функции и многочлены Холла, Oxford Mathematical Monographs (2-е изд.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR  1354144, архивировано из оригинала 2012-12-11
• Окада, Соичи (1998), «Применение формул минорного суммирования к представлениям классических групп в форме прямоугольника», Журнал алгебры , 205 (2): 337–367, doi : 10.1006/jabr.1997.7408 , ISSN  0021-8693, MR  1632816
• Робинсон, Г. де Б. (1938), «О представлениях симметрической группы», American Journal of Mathematics , 60 (3), Издательство Университета Джонса Хопкинса: 745–760, doi : 10.2307/2371609, ISSN  0002-9327, JSTOR  2371609 Збл 0019.25102
• Schensted, C. (1961), «Самые длинные возрастающие и убывающие подпоследовательности», Canadian Journal of Mathematics , 13 : 179–191, doi : 10.4153/CJM-1961-015-3 , ISSN  0008-414X, MR  0121305
• Шютценбергер, член парламента (1963), «Quelques remarques sur une Construction de Schensted», Mathematica Scandinavica , 12 : 117–128, doi : 10.7146/math.scand.a-10676 , ISSN  0025-5521, MR  0190017
• Шютценбергер, Марсель-Поль (1977), «Переписка Робинсона», Combinatoire et représentation du groupe symétrique (Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Страсбург, 1976) , Конспекты лекций по математике, том. 579, Берлин, Нью-Йорк: Springer-Verlag , стр. 59–113, doi : 10.1007/BFb0090012, ISBN. 978-3-540-08143-2, МР  0498826
• Стембридж, Джон Р. (2002), «Краткое доказательство правила Литтлвуда-Ричардсона» (PDF) , Electronic Journal of Combinatorics , 9 (1): Примечание 5, 4 стр. (электронный), doi : 10.37236/1666 , ISSN  1077-8926, MR  1912814
• Томас, Глэнфрвд П. (1974), Алгебры Бакстера и функции Шура , докторская диссертация, Суонси: Университетский колледж Суонси
• van Leeuwen, Marc AA (2001), «Правило Литтлвуда-Ричардсона и связанная с ним комбинаторика» (PDF) , Взаимодействие комбинаторики и теории представлений , MSJ Mem., т. 11, Токио: Math. Soc. Japan, стр. 95–145, MR  1862150
• Зелевинский, А.В. (1981), «Обобщение правила Литтлвуда-Ричардсона и соответствия Робинсона-Шенстеда-Кнута», Журнал алгебры , 69 (1): 82–94, doi : 10.1016/0021-8693(81)90128-9 , ISSN  0021-8693, MR  0613858

Внешние ссылки

• Онлайн-программа, разлагающая произведения функций Шура с использованием правила Литтлвуда–Ричардсона