Мультидерево

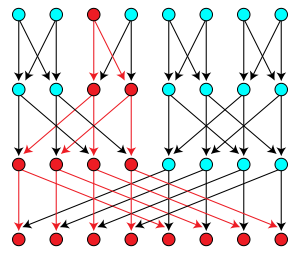
В комбинаторике и теории порядка мультидерево может описывать одну из двух эквивалентных структур: ориентированный ациклический граф (DAG), в котором между любыми двумя вершинами существует не более одного направленного пути , или, что эквивалентно , в котором подграф, достижимый из любой вершины, индуцирует неориентированное дерево , или частично упорядоченное множество (посет), которое не имеет четырех элементов $a$ , $b$ , $c$ и $d,$ образующих ромбовидный подпорядок с $a$ $\leq$ $b$ $\leq$ $d$ и $a$ $\leq$ $c$ $\leq$ $d,$ но с $b$ и $c,$ несравнимыми друг с другом (также называемое ромбовидным посетом ^[1] ).

В теории вычислительной сложности мультидеревья также называются строго однозначными графами или мангровыми деревьями ; их можно использовать для моделирования недетерминированных алгоритмов , в которых существует не более одного вычислительного пути, соединяющего любые два состояния. ^[2]

Мультидеревья могут использоваться для представления нескольких перекрывающихся таксономий на одном и том же наборе оснований. ^[3] Если генеалогическое древо может содержать несколько браков из одной семьи в другую, но не содержит браков между любыми двумя кровными родственниками, то оно образует мультидерево. ^[4]

Эквивалентность определений DAG и частично упорядоченных множеств

В направленном ациклическом графе, если между любыми двумя вершинами существует не более одного направленного пути или, что эквивалентно, если подграф, достижимый из любой вершины, индуцирует неориентированное дерево, то его отношение достижимости является частичным порядком без алмазов. Наоборот, в частичном порядке без алмазов транзитивная редукция определяет направленный ациклический граф, в котором подграф, достижимый из любой вершины, индуцирует неориентированное дерево.

Семьи без алмазов

Семейство множеств без алмазов — это семейство множеств F , включение которых образует частично упорядоченное множество без алмазов. Если D ( n ) обозначает наибольшее возможное семейство подмножеств без алмазов множества из n элементов, то известно, что

2\leq \lim _{n\to \infty }D(n){\Big /}{\binom {n}{\lfloor n/2\rfloor }}\leq 2{\frac {3}{11}}

и предполагается, что предел равен 2. ^[1]

Связанные структуры

Полидерево — ориентированный ациклический граф, образованный путем ориентирования ребер неориентированного дерева, является частным случаем мультидерева.

Подграф, достижимый из любой вершины мультидерева, представляет собой древовидную структуру с корнем в вершине, то есть полидерево, в котором все ребра ориентированы от корня.

Слово «мультидерево» также использовалось для обозначения последовательно - параллельного частичного порядка ^[5] или других структур, образованных путем объединения нескольких деревьев.

Ссылки

^ ab Griggs, Jerrold R.; Li, Wei-Tian; Lu, Linyuan (2010), Семейства без алмазов , arXiv : 1010.5311 , Bibcode : 2010arXiv1010.5311G.
^ Аллендер, Эрик ; Ланге, Клаус-Йорн (1996), "StUSPACE(log n ) ⊆ DSPACE(log ²n /log log n )", Алгоритмы и вычисления, 7-й Международный симпозиум, ISAAC '96, Осака, Япония, 16–18 декабря 1996 г., Труды , Заметки лекций по информатике, т. 1178, Springer-Verlag, стр. 193–202, doi :10.1007/BFb0009495 .
^ Фурнас, Джордж У .; Закс, Джефф (1994), «Мультидеревья: обогащение и повторное использование иерархической структуры», Труды конференции SIGCHI по человеческому фактору в вычислительных системах (CHI '94) , стр. 330–336, doi : 10.1145/191666.191778 , S2CID 18710118.
^ МакГаффин, Майкл Дж.; Балакришнан, Равин (2005), «Интерактивная визуализация генеалогических графов», Симпозиум IEEE по визуализации информации , Лос-Аламитос, Калифорния, США: IEEE Computer Society, стр. 3, doi : 10.1109/INFOVIS.2005.22, S2CID 15449409.
^ Юнг, HA (1978), «О классе частично упорядоченных множеств и соответствующих графах сравнимости», Журнал комбинаторной теории, Серия B , 24 (2): 125–133, doi : 10.1016/0095-8956(78)90013-8 , MR 0491356.