Идеальная хеш-функция

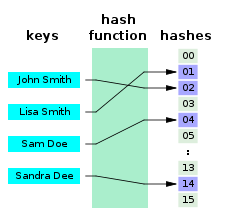
В информатике идеальная хэш-функция $h$ для множества $S$ — это хэш-функция , которая отображает отдельные элементы в $S$ в множество из $m$ целых чисел без коллизий . В математических терминах это инъективная функция .

Идеальные хэш-функции могут использоваться для реализации таблицы поиска с постоянным временем доступа в худшем случае. Идеальная хэш-функция, как и любая хэш-функция , может использоваться для реализации хэш-таблиц , с тем преимуществом, что не требуется реализовывать разрешение коллизий . Кроме того, если ключи отсутствуют в данных и если известно, что запрашиваемые ключи будут действительными, то ключи не нужно хранить в таблице поиска, что экономит место.

Недостатки идеальных хеш-функций в том, что для построения идеальной хеш-функции необходимо знать $S.$ Нединамические идеальные хеш-функции необходимо перестраивать, если $S$ изменяется. Для часто изменяющихся $S можно использовать$ динамические идеальные хеш-функции за счет дополнительного пространства. ^[1] Требуемое пространство для хранения идеальной хеш-функции составляет $O (n),$ где $n$ — количество ключей в структуре.

Важными параметрами производительности идеальных хеш-функций являются время вычисления, которое должно быть постоянным, время построения и размер представления.

Приложение

Идеальная хэш-функция со значениями в ограниченном диапазоне может использоваться для эффективных операций поиска, помещая ключи из $S$ (или другие связанные значения) в таблицу поиска, индексированную выходными данными функции. Затем можно проверить, присутствует ли ключ в $S$ , или найти значение, связанное с этим ключом, найдя его в его ячейке таблицы. Каждый такой поиск занимает постоянное время в худшем случае . ^[2] При идеальном хэшировании связанные данные могут быть прочитаны или записаны с помощью одного доступа к таблице. ^[3]

Производительность идеальных хеш-функций

Важными параметрами производительности для идеального хеширования являются размер представления, время оценки, время построения и, кроме того, требование к диапазону (среднее количество сегментов на ключ в хеш-таблице). ^[4] Время оценки может быть таким же быстрым, как $O$ $($ $1$ $)$ , что является оптимальным. ^[2]^[4] Время построения должно быть не менее $O$ $($ $n$ $)$ , поскольку каждый элемент в $S$ должен быть рассмотрен, а $S$ содержит $n$ элементов. Эта нижняя граница может быть достигнута на практике. ^[4] ${\frac {м}{н}}$

Нижняя граница размера представления зависит от $m$ и $n$ . Пусть $m = (1+ε) n$ и $h$ — идеальная хэш-функция. Хорошее приближение для нижней границы — Биты на элемент. Для минимального идеального хэширования, $ε = 0$ , нижняя граница — $log e \approx 1,44$ бита на элемент. ^[4] $\log e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}$

Строительство

Идеальная хеш-функция для определенного множества $S$ , которая может быть оценена за постоянное время и со значениями в небольшом диапазоне, может быть найдена рандомизированным алгоритмом за ряд операций, пропорциональных размеру S. Оригинальная конструкция Фредмана, Комлоша и Семереди (1984) использует двухуровневую схему для отображения множества $S$ из $n$ элементов в диапазон индексов $O (n)$ , а затем отображает каждый индекс в диапазон значений хеш-функции. Первый уровень их конструкции выбирает большое простое число $p$ (больше размера вселенной, из которой взято $S ), и параметр$ $k$ , и отображает каждый элемент $x$ из $S$ в индекс

g(x)=(kx{\bmod {p}}){\bmod {n}}.

Если $k$ выбирается случайным образом, этот шаг, скорее всего, будет иметь коллизии, но число элементов $n i$ , которые одновременно отображаются в один и тот же индекс $i ,$ скорее всего, будет небольшим. Второй уровень их построения назначает непересекающиеся диапазоны $O (n i 2)$ целых чисел каждому индексу $i$ . Он использует второй набор линейных модульных функций, по одному для каждого индекса $i$ , для отображения каждого члена $x$ из $S$ в диапазон, связанный с $g (x)$ . ^[2]

Как показывают Фредман, Комлош и Семереди (1984), существует выбор параметра $k,$ такой что сумма длин диапазонов для $n$ различных значений $g (x)$ равна $O (n)$ . Кроме того, для каждого значения $g (x)$ существует линейная модульная функция, которая отображает соответствующее подмножество $S$ в диапазон, связанный с этим значением. Как $k$ , так и функции второго уровня для каждого значения $g (x)$ , могут быть найдены за полиномиальное время путем случайного выбора значений до тех пор, пока не будет найдено то, которое работает. ^[2]

Сама хэш-функция требует дискового пространства $O (n)$ для хранения $k$ , $p$ и всех линейных модульных функций второго уровня. Вычисление хэш-значения заданного ключа $x$ может быть выполнено за постоянное время путем вычисления $g (x)$ , поиска функции второго уровня, связанной с $g (x)$ , и применения этой функции к $x$ . Модифицированная версия этой двухуровневой схемы с большим количеством значений на верхнем уровне может быть использована для построения идеальной хэш-функции, которая отображает $S$ в меньший диапазон длины $n + o (n)$ . ^[2]

Более поздний метод построения идеальной хэш-функции описан Белаццуги, Ботельо и Дицфельбингером (2009) как «хэш, смещение и сжатие». Здесь хэш-функция первого уровня $g$ также используется для отображения элементов в диапазон целых чисел $r$ . Элемент $x \in S$ хранится в Bucket $B g(x)$ . ^[4]

Затем, в порядке убывания размера, элементы каждого ведра хэшируются хэш-функцией последовательности независимых полностью случайных хэш-функций $(Φ 1, Φ 2, Φ 3, ...)$ , начиная с $Φ 1$ . Если хэш-функция не создает никаких коллизий для ведра, а полученные значения еще не заняты другими элементами из других ведер, функция выбирается для этого ведра. Если нет, проверяется следующая хэш-функция в последовательности. ^[4]

Чтобы оценить идеальную хеш-функцию $h (x),$ нужно только сохранить отображение σ индекса контейнера $g (x)$ на правильную хеш-функцию в последовательности, в результате чего $h(x) = Φ σ(g(x))$ . ^[4]

Наконец, для уменьшения размера представления ( $σ(i)) 0 \leq i < r$ сжимаются в форму, которая по-прежнему допускает оценку за $O (1)$ . ^[4]

Этот подход требует линейного времени по $n$ для построения и постоянного времени оценки. Размер представления составляет $O (n)$ и зависит от достигнутого диапазона. Например, при $m = 1,23 n$ Belazzougui, Botelho & Dietzfelbinger (2009) достигли размера представления между 3,03 бит/ключ и 1,40 бит/ключ для их приведенного в качестве примера набора из 10 миллионов записей, при этом более низкие значения требуют большего времени вычисления. Нижняя граница пространства в этом сценарии составляет 0,88 бит/ключ. ^[4]

Псевдокод

Алгоритм  хеширования, смещения и сжатия  :
(1) Разбить S на блоки  $B i := g -1 ({i}) \cap S, 0 \leq i < r$ 
(2) Сортировать блоки B _i в порядке убывания в соответствии с размером |B _i |(3) Инициализируем массив T[0...m-1] нулями(4) для всех i  ∈[r], в порядке из (2), выполнить
(5) для l  ←  1,2,...(6) повторить формирование K _i  ←  {  $Φ$ _l (x)|x  ∈  B _i }(6) до тех пор, пока |K _i |=|B _i | и K _i ∩{j|T[j]=1}=  ∅(7) пусть σ(i):= успешный l(8) для всех j  ∈  K _i пусть T[j]:=  1(9) Преобразовать (σ _i ) _0≤i<r в сжатую форму, сохраняя  $O (1)$  доступ.

Нижние границы пространства

Использование $O (n)$ слов информации для хранения функции Фредмана, Комлоша и Семереди (1984) является близким к оптимальному: любая идеальная хеш-функция, которая может быть вычислена за постоянное время, требует по крайней мере количества бит, пропорционального размеру $S$ . ^[5]

Для минимальных совершенных хеш-функций нижняя граница теоретико-информационного пространства равна

\log _{2}e\приблизительно 1,44

бит/ключ. ^[4]

Для идеальных хеш-функций сначала предполагается, что диапазон $h$ ограничен $n$ как $m = (1+ε) n$ . С формулой, данной Белаццуги, Ботельо и Дицфельбингером (2009), и для вселенной , размер которой $|$ $U$ $| =$ $u$ стремится к бесконечности, нижние границы пространства равны $U\supseteq S$

\log _{2}e-\varepsilon \log {\frac {1+\varepsilon }{\varepsilon }}

бит/ключ, минус $log(n)$ бит в целом. ^[4]

Расширения

Идентификация адреса памяти

Тривиальный, но распространенный пример идеального хеширования подразумевается в адресном пространстве (виртуальной) памяти компьютера. Поскольку каждый байт виртуальной памяти является отдельным, уникальным, напрямую адресуемым местом хранения, значение начального адреса , где любой объект хранится в памяти, можно считать фактически идеальным хешем этого объекта во всем диапазоне адресов памяти. ^[6]

Динамическое идеальное хеширование

Использование идеальной хэш-функции лучше всего подходит в ситуациях, когда есть часто запрашиваемый большой набор $S$ , который редко обновляется. Это связано с тем, что любое изменение набора $S$ может привести к тому, что хэш-функция перестанет быть идеальной для измененного набора. Решения, которые обновляют хэш-функцию каждый раз, когда набор изменяется, известны как динамическое идеальное хэширование ^[1] , но эти методы относительно сложны в реализации.

Минимальная идеальная хеш-функция

Минимальная совершенная хеш-функция — это совершенная хеш-функция, которая отображает $n$ ключей в $n$ последовательных целых чисел — обычно числа от $0$ до $n - 1$ или от $1$ до $n$ . Более формальный способ выражения этого таков: пусть $j$ и $k$ — элементы некоторого конечного множества $S$ . Тогда $h$ является минимальной совершенной хеш-функцией тогда и только тогда, когда $h (j) = h (k)$ подразумевает $j = k$ ( инъективность ) и существует целое число $a$ такое, что диапазон $h$ равен $a .. a + | S | - 1$ . Было доказано, что для минимальной совершенной хеш-схемы общего назначения требуется не менее бит/ключ. ^[4] Предполагая, что — набор размера, содержащий целые числа в диапазоне , известно, как эффективно построить явную минимальную совершенную хеш-функцию от до , которая использует биты пространства и которая поддерживает постоянное время вычисления. ^[7] На практике существуют минимальные совершенные хеш-схемы, которые используют примерно 1,56 бит/ключ, если дано достаточно времени. ^[8] $\log _{2}e\приблизительно 1,44$ $S$ $n$ $[1,2^{o(n)}]$ $S$ $\{1,2,\ldots ,n\}$ $n\log _{2}e+o(n)$

k-совершенное хеширование

Хэш-функция является $k$ -совершенной, если не более $k$ элементов из $S$ отображаются на одно и то же значение в диапазоне. Алгоритм «хеш, смещение и сжатие» может быть использован для построения $k$ -совершенных хеш-функций, допуская до $k$ коллизий. Изменения, необходимые для достижения этого, минимальны и подчеркнуты в адаптированном псевдокоде ниже:

(4) для всех i  ∈[r], в порядке из (2), выполнить
(5) для l  ←  1,2,...(6) повторить формирование K _i  ←  {  $Φ$ _l (x)|x  ∈  B _i }(6) до тех пор, пока |K _i |=|B _i | и K _i ∩{j| T[j]=k }=  ∅(7) пусть σ(i):= успешный l(8) для всех j  ∈  K _i положим  T[j]←T[j]+1

Сохранение заказа

Минимальная совершенная хэш-функция $F$ сохраняет порядок, если ключи заданы в некотором порядке $a 1, a 2, ..., a n$ и для любых ключей $a j$ и $a k$ , $j < k$ подразумевает $F (a j) < F(a k)$ . ^[9] В этом случае значение функции — это просто позиция каждого ключа в отсортированном порядке всех ключей. Простая реализация сохраняющих порядок минимальных совершенных хэш-функций с постоянным временем доступа заключается в использовании (обычной) совершенной хэш-функции для хранения таблицы поиска позиций каждого ключа. Это решение использует биты, что оптимально в условиях, когда функция сравнения для ключей может быть произвольной. ^[10] Однако, если ключи $a$ $1$ $,$ $a$ $2$ $, ...,$ $a$ $n$ являются целыми числами, взятыми из вселенной , то можно построить сохраняющую порядок хэш-функцию, используя только биты пространства. ^[11] Более того, известно, что эта граница является оптимальной. ^[12] $O(n\log n)$ $\{1,2,\ldots ,U\}$ $O(n\log \log \log U)$

Связанные конструкции

В то время как хорошо размерные хэш-таблицы имеют амортизированное среднее время O(1) (амортизированное среднее постоянное время) для поиска, вставки и удаления, большинство алгоритмов хэш-таблиц страдают от возможных худших времен, которые занимают гораздо больше времени. Худшее время O(1) (постоянное время даже в худшем случае) было бы лучше для многих приложений (включая сетевой маршрутизатор и кэши памяти ). ^[13]^{: 41}

Немногие алгоритмы хэш-таблиц поддерживают худшее время поиска O(1) (постоянное время поиска даже в худшем случае). Вот некоторые из них: идеальное хэширование; динамическое идеальное хэширование ; хэширование кукушкой ; хэширование классиками ; и расширяемое хэширование . ^[13]^{: 42–69}

Простая альтернатива идеальному хешированию, которая также допускает динамические обновления, — это хеширование кукушки . Эта схема сопоставляет ключи с двумя или более локациями в пределах диапазона (в отличие от идеального хеширования, которое сопоставляет каждый ключ с одной локацией), но делает это таким образом, что ключи могут быть назначены один к одному локациям, с которыми они были сопоставлены. Поиск с этой схемой медленнее, поскольку необходимо проверить несколько локаций, но тем не менее занимает постоянное время в худшем случае. ^[14]

Ссылки

^ аб Дитцфельбингер, Мартин; Карлин, Анна ; Мельхорн, Курт ; Мейер ауф дер Хайде, Фридхельм; Ронерт, Ганс; Тарьян, Роберт Э. (1994), «Динамическое идеальное хеширование: верхняя и нижняя границы», SIAM Journal on Computing , 23 (4): 738–761, doi : 10.1137/S0097539791194094, MR 1283572.
^ abcde Фредман, Майкл Л .; Комлос, Янош ; Семереди, Эндре (1984), «Хранение разреженной таблицы с временем доступа для наихудшего случая $O$ $(1)$ », Журнал ACM , 31 (3): 538, doi : 10.1145/828.1884 , MR 0819156, S2CID 5399743
^ Лу, Йи; Прабхакар, Баладжи; Бономи, Флавио (2006), «Идеальное хеширование для сетевых приложений», Международный симпозиум IEEE по теории информации 2006 г. , стр. 2774–2778, doi :10.1109/ISIT.2006.261567, ISBN 1-4244-0505-X, S2CID 1494710
^ abcdefghijkl Белаццуги, Джамаль; Ботельо, Фабиано К.; Дитцфельбингер, Мартин (2009), «Хеширование, перемещение и сжатие» (PDF) , Алгоритмы - ESA 2009 (PDF) , Конспекты лекций по информатике , том. 5757, Берлин: Springer, стр. 682–693, CiteSeerX 10.1.1.568.130 , doi : 10.1007/978-3-642-04128-0_61, ISBN 978-3-642-04127-3, г-н 2557794.
^ Фредман, Майкл Л.; Комлош , Янош (1984), «О размере разделяющих систем и семействах совершенных хэш-функций», SIAM Journal on Algebraic and Discrete Methods , 5 (1): 61–68, doi :10.1137/0605009, MR 0731857.
^ Витольд Литвин; Тадеуш Морзи; Готтфрид Фоссен (19 августа 1998 г.). Достижения в области баз данных и информационных систем. Springer Science+Business Media . стр. 254. ISBN 9783540649243.
^ Хагеруп, Торбен; Толей, Торстен (2001), «Эффективное минимальное совершенное хеширование в почти минимальном пространстве», STACS 2001 , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 317–326, doi :10.1007/3-540-44693-1_28, ISBN 978-3-540-41695-1, получено 2023-11-12
^ Эспозито, Эммануэль; Мюллер Граф, Томас; Винья, Себастьяно (2020), «RecSplit: минимальное идеальное хеширование с помощью рекурсивного разделения», Труды симпозиума по разработке алгоритмов и экспериментам 2020 г. (ALENEX) , Труды , стр. 175–185, arXiv : 1910.06416 , doi : 10.1137/1.9781611976007.14.
↑ Дженкинс, Боб (14 апреля 2009 г.), «минимальное совершенное хеширование с сохранением порядка», в Black, Paul E. (ред.), Dictionary of Algorithms and Data Structures, US National Institute of Standards and Technology , получено 2013-03-05
^ Фокс, Эдвард А.; Чен, Ци Фань; Дауд, Амджад М.; Хит, Ленвуд С. (июль 1991 г.), «Сохраняющие порядок минимальные совершенные хэш-функции и поиск информации» (PDF) , ACM Transactions on Information Systems , 9 (3), Нью-Йорк, штат Нью-Йорк, США: ACM: 281–308, doi :10.1145/125187.125200, S2CID 53239140.
^ Белаццоуги, Джамал; Болди, Паоло; Паг, Расмус ; Винья, Себастьяно (ноябрь 2008 г.), «Теория и практика монотонного минимального совершенного хеширования», Журнал экспериментальной алгоритмики , 16 , статья № 3.2, 26 стр., doi : 10.1145/1963190.2025378, S2CID 2367401.
^ Assadi, Sepehr; Farach-Colton, Martín; Kuszmaul, William (январь 2023 г.), «Жесткие границы для монотонного минимального совершенного хеширования», Труды ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA) 2023 г. , Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, стр. 456–476, arXiv : 2207.10556 , doi : 10.1137/1.9781611977554.ch20, ISBN 978-1-61197-755-4, получено 2023-04-27
^ Тимоти А. Дэвис. "Глава 5 Хеширование": подраздел "Хеш-таблицы с наихудшим случаем доступа O(1)"
^ Паг, Расмус ; Родлер, Флемминг Фриш (2004), «Хеширование с кукушкой», Журнал алгоритмов , 51 (2): 122–144, doi : 10.1016/j.jalgor.2003.12.002, MR 2050140.

Дальнейшее чтение

Ричард Дж. Чикелли. Минимальные совершенные хэш-функции, сделанные простыми , Communications of the ACM, т. 23, номер 1, январь 1980 г.
Томас Х. Кормен , Чарльз Э. Лейзерсон , Рональд Л. Ривест и Клиффорд Стайн . Введение в алгоритмы , третье издание. MIT Press, 2009. ISBN 978-0262033848 . Раздел 11.5: Идеальное хеширование, стр. 267, 277–282.
Фабиано К. Ботельо, Расмус Пах и Нивио Зивиани. «Идеальное хеширование для приложений управления данными».
Фабиано К. Ботельо и Нивио Зивиани . «Внешнее идеальное хеширование для очень больших наборов ключей». 16-я конференция ACM по управлению информацией и знаниями (CIKM07), Лиссабон, Португалия, ноябрь 2007 г.
Джамал Белаццоуги, Паоло Больди, Расмус Паг и Себастьяно Винья. "Монотонное минимальное совершенное хеширование: поиск в отсортированной таблице с доступом O(1)". В трудах 20-го ежегодного симпозиума ACM-SIAM по дискретной математике (SODA), Нью-Йорк, 2009. ACM Press.
Маршалл Д. Брейн и Алан Л. Тарп. «Почти идеальное хеширование больших наборов слов». Software—Practice and Experience, т. 19(10), 967-078, октябрь 1989 г. John Wiley & Sons.
Дуглас К. Шмидт, GPERF: Идеальный генератор хэш-функций, C++ Report, SIGS, т. 10, № 10, ноябрь/декабрь 1998 г.

Внешние ссылки

gperf — это идеальный генератор хешей с открытым исходным кодом для C и C++ (очень быстрый, но работает только для небольших наборов)
Минимальное идеальное хеширование (алгоритм Боба) Боба Дженкинса
cmph: библиотека минимального идеального хэширования на языке C, реализация с открытым исходным кодом для многих (минимальных) идеальных хэшей (работает для больших наборов)
Sux4J: монотонное минимальное идеальное хеширование с открытым исходным кодом в Java
MPHSharp: идеальные методы хеширования в C#
BBHash: минимальная идеальная хэш-функция в C++ только с заголовками
Perfect::Hash, идеальный генератор хешей на Perl, создающий код на языке C. Имеет раздел «Предшествующее искусство», на который стоит обратить внимание.