Групповое тестирование

Процедура, которая разбивает задачу идентификации определенных объектов на тесты по группам предметов.

Иллюстрация задачи с лампочкой, где нужно найти сломанную лампочку среди шести лампочек. Здесь первые три подключены к источнику питания и загораются (A). Это означает, что сломанная лампочка должна быть одной из последних трех (B). Если бы лампочки не загорелись, можно было бы быть уверенным, что сломанная лампочка была среди первых трех. Продолжая эту процедуру, можно найти сломанную лампочку не более чем за три теста, по сравнению с максимум шестью тестами, если лампочки проверяются по отдельности.

В статистике и комбинаторной математике групповое тестирование — это любая процедура, которая разбивает задачу идентификации определенных объектов на тесты по группам элементов, а не по отдельным. Впервые изученное Робертом Дорфманом в 1943 году, групповое тестирование — это относительно новая область прикладной математики, которая может применяться в широком спектре практических приложений и является активной областью исследований сегодня.

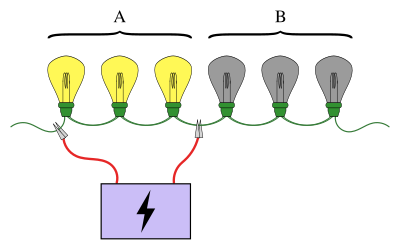
Известный пример группового тестирования включает в себя ряд лампочек, соединенных последовательно, где известно, что ровно одна из лампочек сломана. Цель состоит в том, чтобы найти сломанную лампочку, используя наименьшее количество тестов (где тестом является подключение некоторых лампочек к источнику питания). Простой подход заключается в том, чтобы проверить каждую лампочку по отдельности. Однако, когда лампочек много, было бы гораздо эффективнее объединить лампочки в группы. Например, подключив первую половину лампочек сразу, можно определить, в какой половине находится сломанная лампочка, исключив половину лампочек всего за один тест.

Схемы проведения группового тестирования могут быть простыми или сложными, а тесты, используемые на каждом этапе, могут быть разными. Схемы, в которых тесты для следующего этапа зависят от результатов предыдущих этапов, называются адаптивными процедурами , тогда как схемы, разработанные таким образом, что все тесты известны заранее, называются неадаптивными процедурами . Структура схемы тестов, используемых в неадаптивной процедуре, известна как схема объединения .

Групповое тестирование имеет множество приложений, включая статистику, биологию, информатику, медицину, инженерию и кибербезопасность. Современный интерес к этим схемам тестирования был возрожден проектом « Геном человека» . ^[1]

Основное описание и термины

В отличие от многих областей математики, истоки группового тестирования можно проследить до одного отчета ^[2], написанного одним человеком: Робертом Дорфманом . ^[3] Мотивация возникла во время Второй мировой войны, когда Служба общественного здравоохранения США и Служба выборочной службы приступили к масштабному проекту по отсеиванию всех мужчин , больных сифилисом, призванных на призыв. Тестирование человека на сифилис включает в себя взятие у него образца крови, а затем анализ образца для определения наличия или отсутствия сифилиса. В то время проведение этого теста было дорогим, и тестирование каждого солдата по отдельности было бы очень дорогим и неэффективным. ^[3]

Предположим, что есть солдаты, этот метод тестирования приводит к отдельным тестам. Если большая часть людей инфицирована, то этот метод был бы разумным. Однако в более вероятном случае, когда инфицирована только очень небольшая часть мужчин, можно достичь гораздо более эффективной схемы тестирования. Осуществимость более эффективной схемы тестирования зависит от следующего свойства: солдат можно объединить в группы, и в каждой группе образцы крови можно объединить. Затем объединенный образец можно проверить, есть ли хотя бы у одного солдата в группе сифилис. Это центральная идея группового тестирования. Если у одного или нескольких солдат в этой группе сифилис, то тест напрасный (необходимо провести больше тестов, чтобы определить, какой солдат это был). С другой стороны, если ни у кого в пуле нет сифилиса, то экономится много тестов, поскольку каждый солдат в этой группе может быть исключен всего одним тестом. ^[3] ${\displaystyle n}$ ${\displaystyle n}$

Предметы, которые вызывают положительный результат теста группы, обычно называются дефектными предметами (это разбитые лампочки, сифилитики и т. д.). Часто общее количество предметов обозначается как и представляет собой количество дефектных, если предполагается, что оно известно. ^[3] ${\displaystyle n}$ ${\displaystyle d}$

Классификация задач группового тестирования

Существуют две независимые классификации задач группового тестирования: каждая задача группового тестирования является либо адаптивной, либо неадаптивной, а также вероятностной или комбинаторной. ^[3]

В вероятностных моделях предполагается, что дефектные элементы следуют некоторому распределению вероятностей , и цель состоит в том, чтобы минимизировать ожидаемое количество тестов, необходимых для определения дефектности каждого элемента. С другой стороны, при комбинаторном групповом тестировании цель состоит в том, чтобы минимизировать количество тестов, необходимых в «худшем сценарии» — то есть создать алгоритм minmax — и не предполагается никаких знаний о распределении дефектных элементов. ^[3]

Другая классификация, адаптивность, касается того, какую информацию можно использовать при выборе элементов для группировки в тест. В общем, выбор элементов для тестирования может зависеть от результатов предыдущих тестов, как в приведенной выше задаче с лампочкой. Алгоритм, который выполняется путем выполнения теста, а затем использования результата (и всех прошлых результатов) для принятия решения о том, какой следующий тест выполнить, называется адаптивным. Наоборот, в неадаптивных алгоритмах все тесты определяются заранее. Эту идею можно обобщить на многоэтапные алгоритмы, где тесты делятся на этапы, и каждый тест на следующем этапе должен быть определен заранее, зная только результаты тестов на предыдущих этапах. Хотя адаптивные алгоритмы предлагают гораздо большую свободу в разработке, известно, что адаптивные алгоритмы группового тестирования не улучшают неадаптивные более чем на постоянный множитель в количестве тестов, необходимых для идентификации набора дефектных элементов. ^{[4] [3]} В дополнение к этому, неадаптивные методы часто полезны на практике, поскольку можно приступить к последовательным тестам без предварительного анализа результатов всех предыдущих тестов, что позволяет эффективно распределить процесс тестирования.

Вариации и расширения

Существует много способов расширить проблему группового тестирования. Один из самых важных называется шумным групповым тестированием и имеет дело с большим предположением исходной проблемы: что тестирование безошибочно. Проблема группового тестирования называется шумной, когда есть некоторая вероятность того, что результат группового тестирования ошибочен (например, оказывается положительным, когда тест не содержал дефектных элементов). Модель шума Бернулли предполагает, что эта вероятность является некоторой константой, , но в целом она может зависеть от истинного числа дефектных элементов в тесте и числа протестированных элементов. ^[5] Например, эффект разбавления можно смоделировать, сказав, что положительный результат более вероятен, когда в тесте присутствует больше дефектных элементов (или больше дефектных элементов как доля от числа протестированных элементов). ^[6] Шумный алгоритм всегда будет иметь ненулевую вероятность совершения ошибки (то есть неправильной маркировки элемента). ${\displaystyle q}$

Групповое тестирование может быть расширено путем рассмотрения сценариев, в которых существует более двух возможных результатов теста. Например, тест может иметь результаты и , что соответствует отсутствию дефектов, одному дефекту или неизвестному числу дефектов, большему, чем один. В более общем смысле, можно считать, что набор результатов теста для некоторых . ^[3] ${\displaystyle 0,1}$ ${\displaystyle 2^{+}}$ ${\displaystyle {0,1,\ldots ,k^{+}}}$ ${\displaystyle k\in \mathbb {N} }$

Другое расширение заключается в рассмотрении геометрических ограничений на то, какие наборы могут быть протестированы. Вышеуказанная задача о лампочке является примером такого рода ограничений: можно протестировать только те лампочки, которые появляются последовательно. Аналогично, элементы могут быть расположены по кругу или, в общем случае, в сети, где тесты являются доступными путями на графике. Другой вид геометрического ограничения будет касаться максимального количества элементов, которые могут быть протестированы в группе, ^[a] или размеры групп могут быть четными и т. д. Аналогичным образом, может быть полезно рассмотреть ограничение, что любой данный элемент может появляться только в определенном количестве тестов. ^[3]

Существует бесконечное множество способов продолжать переделывать базовую формулу группового тестирования. Следующие пояснения дадут представление о некоторых более экзотических вариантах. В модели «хорошо–посредственно–плохо» каждый элемент является одним из «хорошо», «посредственно» или «плохо», а результат теста — это тип «худшего» элемента в группе. В пороговом групповом тестировании результат теста положителен, если количество дефектных элементов в группе больше некоторого порогового значения или пропорции. ^[7] Групповое тестирование с ингибиторами — это вариант, имеющий применение в молекулярной биологии. Здесь есть третий класс элементов, называемых ингибиторами, и результат теста положителен, если он содержит хотя бы один дефектный элемент и не содержит ингибиторов. ^[8]

История и развитие

Изобретение и начальный прогресс

Концепция группового тестирования была впервые введена Робертом Дорфманом в 1943 году в кратком отчете ^[2], опубликованном в разделе «Заметки» журнала Annals of Mathematical Statistics . ^{[3] [b]} Отчет Дорфмана — как и все ранние работы по групповому тестированию — был сосредоточен на вероятностной проблеме и был направлен на использование новой идеи группового тестирования для сокращения ожидаемого количества тестов, необходимых для отсеивания всех мужчин с сифилисом среди заданной группы солдат. Метод был прост: солдаты были разделены на группы заданного размера и применялось индивидуальное тестирование (тестирование предметов в группах размером один) на положительных группах, чтобы определить, какие из них были инфицированы. Дорфман составил таблицу оптимальных размеров групп для этой стратегии в зависимости от уровня распространенности дефектности в популяции. ^[2] Стивен Сэмюэлс ^[10] нашел решение в замкнутой форме для оптимального размера группы как функции уровня распространенности.

После 1943 года групповое тестирование оставалось в значительной степени неизменным в течение ряда лет. Затем в 1957 году Стерретт усовершенствовал процедуру Дорфмана. ^[11] Этот новый процесс начинается с повторного проведения индивидуального тестирования на положительных группах, но останавливается, как только обнаруживается дефектный. Затем оставшиеся элементы в группе проверяются вместе, поскольку весьма вероятно, что ни один из них не является дефектным.

Первое тщательное рассмотрение группового тестирования было дано Собелем и Гроллом в их основополагающей статье 1959 года по этому вопросу. ^[12] Они описали пять новых процедур — в дополнение к обобщениям для случаев, когда уровень распространенности неизвестен — и для оптимальной процедуры они предоставили явную формулу для ожидаемого числа тестов, которые она будет использовать. В статье также впервые была установлена ​​связь между групповым тестированием и теорией информации , а также обсуждались несколько обобщений проблемы группового тестирования и предлагались некоторые новые приложения теории.

Фундаментальный результат Питера Унгара в 1960 году показывает, что если уровень распространенности , то индивидуальное тестирование является оптимальной процедурой группового тестирования относительно ожидаемого числа тестов, а если , то оно не является оптимальным. Однако важно отметить, что, несмотря на 80 лет исследовательских усилий, оптимальная процедура до сих пор неизвестна для и общего размера популяции . ^[13] ${\displaystyle p>p_{u}=(3-{\sqrt {5}})/2\approx 0.38}$ ${\displaystyle p<p_{u}}$ ${\displaystyle p<p_{u}}$ ${\displaystyle n>2}$

Комбинаторное групповое тестирование

Групповое тестирование впервые было изучено в комбинаторном контексте Ли в 1962 году ^[14] с введением алгоритма Ли -stage ${\displaystyle s}$ . ^[3] Ли предложил расширение «алгоритма 2-stage» Дорфмана до произвольного числа этапов, которое требовало не более тестов, чтобы гарантированно найти или меньше дефектных элементов. Идея состояла в том, чтобы удалить все элементы с отрицательными тестами и разделить оставшиеся элементы на группы, как это было сделано с исходным пулом. Это должно было быть сделано несколько раз перед выполнением индивидуального тестирования. ${\displaystyle t={\frac {e}{\log _{2}(e)}}d\log _{2}(n)}$ ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle s-1}$

Комбинаторное групповое тестирование в целом было позднее более полно изучено Катоной в 1973 году. ^[15] Катона ввел матричное представление неадаптивного группового тестирования и разработал процедуру поиска дефекта в неадаптивном 1-дефектном случае не более чем за тесты, которую он также доказал как оптимальную. ${\displaystyle t=\lceil \log _{2}(n)\rceil }$

В целом, поиск оптимальных алгоритмов для адаптивного комбинаторного группового тестирования является сложной задачей, и хотя вычислительная сложность группового тестирования не была определена, предполагается, что она является сложной в некотором классе сложности. ^[3] Однако важный прорыв произошел в 1972 году с введением обобщенного алгоритма двоичного разбиения. ^[16] Обобщенный алгоритм двоичного разбиения работает путем выполнения бинарного поиска в группах, которые дают положительный результат теста, и является простым алгоритмом, который находит один дефектный не более чем за количество тестов, ограниченное нижней границей информации.

В сценариях, где есть два или более дефектных, обобщенный алгоритм бинарного разделения все еще дает почти оптимальные результаты, требуя в большинстве случаев тестов выше нижней границы информации, где — количество дефектных. ^[16] Значительные улучшения в этом отношении были сделаны в 2013 году Аллеманом, который получил необходимое количество тестов меньше, чем выше нижней границы информации, когда и . ^[17] Это было достигнуто путем изменения бинарного поиска в алгоритме бинарного разделения на сложный набор подалгоритмов с перекрывающимися тестовыми группами. Таким образом, проблема адаптивного комбинаторного группового тестирования — с известным числом или верхней границей количества дефектных — по сути, была решена, с небольшими возможностями для дальнейшего улучшения. ${\displaystyle d-1}$ ${\displaystyle d}$ ${\displaystyle 0.187d+0.5\log _{2}(d)+5.5}$ ${\displaystyle n/d\geq 38}$ ${\displaystyle d\geq 10}$

Остается открытым вопрос о том, когда индивидуальное тестирование является minmax . Ху, Хван и Ван показали в 1981 году, что индивидуальное тестирование является minmax, когда , и что оно не является minmax, когда . ^[18] В настоящее время предполагается, что эта граница является точной: то есть индивидуальное тестирование является minmax тогда и только тогда, когда . ^{[19] [c]} Некоторый прогресс был достигнут в 2000 году Риччио и Колборном, которые показали, что для больших индивидуальное тестирование является minmax, когда . ^[20] ${\displaystyle n\leq \lfloor (5d+1)/2\rfloor }$ ${\displaystyle n>3d}$ ${\displaystyle n\leq 3d}$ ${\displaystyle n}$ ${\displaystyle d\geq n/\log _{3/2}(3)\approx 0.369n}$

Неадаптивное и вероятностное тестирование

Одно из ключевых открытий в неадаптивном групповом тестировании заключается в том, что можно добиться значительных успехов, устранив требование, чтобы процедура группового тестирования была гарантированно успешной («комбинаторная» проблема), а вместо этого разрешив ей иметь некоторую низкую, но ненулевую вероятность неправильной маркировки каждого элемента («вероятностная» проблема). Известно, что по мере того, как количество дефектных элементов приближается к общему количеству элементов, точные комбинаторные решения требуют значительно большего количества тестов, чем вероятностные решения — даже вероятностные решения допускают только асимптотически малую вероятность ошибки. ^{[4] [d]}

В этом ключе Чан и др. (2011) представили COMP — вероятностный алгоритм, который требует не более тестов для обнаружения дефектных элементов с вероятностью ошибки не более . ^[5] Это находится в пределах постоянного множителя нижней границы. ^[4] ${\displaystyle t=ed(1+\delta )\ln(n)}$ ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle n^{-\delta }}$ ${\displaystyle t=O(d\log _{2}n)}$

Чан и др. (2011) также представили обобщение COMP для простой шумной модели и аналогичным образом вывели явную границу производительности, которая снова была только константой (зависящей от вероятности неудачного теста) выше соответствующей нижней границы. ^{[4] [5]} В общем, количество тестов, требуемых в случае шума Бернулли, является постоянным множителем, большим, чем в случае без шума. ^[5]

Aldridge, Baldassini и Johnson (2014) разработали расширение алгоритма COMP, которое добавило дополнительные шаги постобработки. ^[21] Они показали, что производительность этого нового алгоритма, называемого DD, строго превосходит производительность COMP, и что DD является «по существу оптимальным» в сценариях, где , сравнивая его с гипотетическим алгоритмом, который определяет разумный оптимум. Производительность этого гипотетического алгоритма предполагает, что есть возможности для улучшения, когда , а также предполагает, насколько значительным может быть это улучшение. ^[21] ${\displaystyle d^{2}\geq n}$ ${\displaystyle d^{2}<n}$

Формализация комбинаторного группового тестирования

В этом разделе формально определяются понятия и термины, относящиеся к групповому тестированию.

• Входной вектор , , определяется как двоичный вектор длины (то есть ), причем j -й элемент называется дефектным тогда и только тогда, когда . Кроме того, любой недефектный элемент называется «хорошим» элементом. ${\displaystyle \mathbf {x} =(x_{1},x_{2},\dots ,x_{n})}$ ${\displaystyle n}$ ${\displaystyle \mathbf {x} \in \{0,1\}^{n}}$ ${\displaystyle x_{j}=1}$

${\displaystyle \mathbf {x} }$предназначен для описания (неизвестного) набора дефектных элементов. Ключевое свойство заключается в том, что это неявный ввод . То есть, нет прямого знания о том, что представляют собой записи , кроме того, что можно вывести с помощью некоторой серии «тестов». Это приводит к следующему определению. ${\displaystyle \mathbf {x} }$ ${\displaystyle \mathbf {x} }$

• Пусть будет входным вектором. Набор, называется тестом . Когда тестирование без шума , результат теста положителен , когда существует такое, что , и результат отрицателен в противном случае. ${\displaystyle \mathbf {x} }$ ${\displaystyle S\subseteq \{1,2,\dots ,n\}}$ ${\displaystyle j\in S}$ ${\displaystyle x_{j}=1}$

Таким образом, целью группового тестирования является разработка метода выбора «короткой» серии тестов, позволяющей определить результат либо точно, либо с высокой степенью достоверности. ${\displaystyle \mathbf {x} }$

• Говорят, что алгоритм группового тестирования делает ошибку , если он неправильно маркирует элемент (то есть маркирует любой дефектный элемент как недефектный и наоборот). Это не то же самое, что результат группового тестирования, который является неправильным. Алгоритм называется алгоритмом с нулевой ошибкой , если вероятность того, что он сделает ошибку, равна нулю. ^[e]
• ${\displaystyle t(d,n)}$обозначает минимальное количество тестов, необходимых для того, чтобы всегда находить дефектные элементы среди элементов с нулевой вероятностью ошибки любым алгоритмом группового тестирования. Для того же количества, но с ограничением, что алгоритм неадаптивный, используется обозначение. ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle {\bar {t}}(d,n)}$

Общие границы

Поскольку всегда можно прибегнуть к индивидуальному тестированию, установив для каждого , то должно быть так, что . Кроме того, поскольку любая неадаптивная процедура тестирования может быть записана как адаптивный алгоритм, просто выполняя все тесты без учета их результата, . Наконец, когда , есть по крайней мере один элемент, дефектность которого должна быть определена (по крайней мере одним тестом), и поэтому . ${\displaystyle S_{j}=\{j\}}$ ${\displaystyle 1\leq j\leq n}$ ${\displaystyle {\bar {t}}(d,n)\leq n}$ ${\displaystyle t(d,n)\leq {\bar {t}}(d,n)}$ ${\displaystyle 0\neq d\neq n}$ ${\displaystyle 1\leq t(d,n)}$

Подводя итог (при допущении ), . ^[f] ${\displaystyle 0\neq d\neq n}$ ${\displaystyle 1\leq t(d,n)\leq {\bar {t}}(d,n)\leq n}$

Нижняя граница информации

Нижнюю границу количества необходимых тестов можно описать с помощью понятия пространства выборки , обозначаемого , которое является просто набором возможных размещений дефектных элементов. Для любой задачи группового тестирования с пространством выборки и любым алгоритмом группового тестирования можно показать, что , где — минимальное количество тестов, необходимое для выявления всех дефектных элементов с нулевой вероятностью ошибки. Это называется нижней границей информации . ^[3] Эта граница выводится из того факта, что после каждого теста разделяется на два непересекающихся подмножества, каждое из которых соответствует одному из двух возможных результатов теста. ${\displaystyle {\mathcal {S}}}$ ${\displaystyle {\mathcal {S}}}$ ${\displaystyle t\geq \lceil \log _{2}{|{\mathcal {S}}|}\rceil }$ ${\displaystyle t}$ ${\displaystyle {\mathcal {S}}}$

Однако нижняя граница информации сама по себе обычно недостижима, даже для небольших задач. ^[3] Это происходит потому, что разделение не является произвольным, поскольку оно должно быть реализуемо с помощью некоторого теста. ${\displaystyle {\mathcal {S}}}$

Фактически, нижняя граница информации может быть обобщена на случай, когда существует ненулевая вероятность того, что алгоритм сделает ошибку. В этой форме теорема дает нам верхнюю границу вероятности успеха на основе количества тестов. Для любого алгоритма группового тестирования, который выполняет тесты, вероятность успеха, , удовлетворяет . Это можно усилить до: . ^{[5] [22]} ${\displaystyle t}$ ${\displaystyle \mathbb {P} ({\textrm {success}})}$ ${\displaystyle \mathbb {P} ({\textrm {success}})\leq t/\log _{2}{n \choose d}}$ ${\displaystyle \mathbb {P} ({\textrm {success}})\leq {\frac {2^{t}}{n \choose d}}}$

Представление неадаптивных алгоритмов

Типичная настройка группового тестирования. Неадаптивный алгоритм сначала выбирает матрицу , а затем получает вектор y . Затем задача состоит в том, чтобы найти оценку для x . ${\displaystyle M}$

Алгоритмы для неадаптивного группового тестирования состоят из двух отдельных фаз. Во-первых, решается, сколько тестов выполнить и какие элементы включить в каждый тест. Во второй фазе, часто называемой этапом декодирования, результаты каждого группового теста анализируются, чтобы определить, какие элементы, скорее всего, будут дефектными. Первая фаза обычно кодируется в матрице следующим образом. ^[5]

• Предположим, что неадаптивная процедура группового тестирования для элементов состоит из тестов для некоторых . Матрица тестирования для этой схемы представляет собой бинарную матрицу, , где тогда и только тогда, когда (и равна нулю в противном случае). ${\displaystyle n}$ ${\displaystyle S_{1},S_{2},\dots ,S_{t}}$ ${\displaystyle t\in \mathbb {N} _{\geq 0}}$ ${\displaystyle t\times n}$ ${\displaystyle M}$ ${\displaystyle (M)_{ij}=1}$ ${\displaystyle j\in S_{i}}$

Таким образом, каждый столбец представляет элемент, а каждая строка представляет тест, при этом в записи указывается, что тест включал элемент, а в противном случае — указывается. ${\displaystyle M}$ ${\displaystyle 1}$ ${\displaystyle (i,j){\textrm {-th}}}$ ${\displaystyle i{\textrm {-th}}}$ ${\displaystyle j{\textrm {-th}}}$ ${\displaystyle 0}$

Наряду с вектором (длиной ), описывающим неизвестный дефектный набор, принято вводить вектор результата, описывающий результаты каждого теста. ${\displaystyle \mathbf {x} }$ ${\displaystyle n}$

• Пусть будет числом тестов, выполненных неадаптивным алгоритмом. Вектор результата , , является двоичным вектором длины (то есть ), таким, что тогда и только тогда, когда результат теста был положительным (то есть содержал хотя бы один дефектный). ^[g] ${\displaystyle t}$ ${\displaystyle \mathbf {y} =(y_{1},y_{2},\dots ,y_{t})}$ ${\displaystyle t}$ ${\displaystyle \mathbf {y} \in \{0,1\}^{t}}$ ${\displaystyle y_{i}=1}$ ${\displaystyle i{\textrm {-th}}}$

С этими определениями неадаптивную задачу можно переформулировать следующим образом: сначала выбирается тестовая матрица, , после чего возвращается вектор . Затем задача заключается в анализе для нахождения некоторой оценки для . ${\displaystyle M}$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {x} }$

В простейшем шумном случае, когда существует постоянная вероятность, , что групповой тест будет иметь ошибочный результат, рассматривается случайный двоичный вектор, , где каждая запись имеет вероятность быть , и в противном случае. Вектор, который возвращается, тогда равен , с обычным добавлением (эквивалентно, это поэлементная операция XOR ). Шумный алгоритм должен оценивать с использованием (то есть без прямого знания ). ^[5] ${\displaystyle q}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle q}$ ${\displaystyle 1}$ ${\displaystyle 0}$ ${\displaystyle {\hat {\mathbf {y} }}=\mathbf {y} +\mathbf {v} }$ ${\displaystyle (\mathbb {Z} /2\mathbb {Z} )^{n}}$ ${\displaystyle \mathbf {x} }$ ${\displaystyle {\hat {\mathbf {y} }}}$ ${\displaystyle \mathbf {y} }$

Границы для неадаптивных алгоритмов

Матричное представление позволяет доказать некоторые границы неадаптивного группового тестирования. Подход отражает подход многих детерминированных конструкций, где рассматриваются -разделимые матрицы, как определено ниже. ^[3] ${\displaystyle d}$

• Двоичная матрица, , называется -разделимой, если каждая булева сумма (логическое ИЛИ) любого из ее столбцов различна. Кроме того, обозначение -разделимая указывает, что каждая сумма любого из до из столбцов ' различна. (Это не то же самое, что быть -разделимым для каждого .) ${\displaystyle M}$ ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle {\bar {d}}}$ ${\displaystyle d}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle k}$ ${\displaystyle k\leq d}$

Когда является проверочной матрицей, свойство быть -разделимым ( -separable) эквивалентно способности различать (до) дефектных. Однако это не гарантирует, что это будет просто. Более сильное свойство, называемое дизъюнктностью , делает это. ${\displaystyle M}$ ${\displaystyle d}$ ${\displaystyle {\bar {d}}}$ ${\displaystyle d}$

• Двоичная матрица называется -дизъюнктной , если булева сумма любых столбцов не содержит никаких других столбцов. (В этом контексте говорят, что столбец A содержит столбец B, если для каждого индекса, где B имеет 1, A также имеет 1.) ${\displaystyle M}$ ${\displaystyle d}$ ${\displaystyle d}$

Полезное свойство -дизъюнктных матриц тестирования заключается в том, что при наличии до дефектных элементов каждый недефектный элемент появится хотя бы в одном тесте с отрицательным результатом. Это означает, что существует простая процедура поиска дефектных элементов: просто удалите каждый элемент, который появляется в отрицательном тесте. ${\displaystyle d}$ ${\displaystyle d}$

Используя свойства -разделимых и -дизъюнктных матриц, можно показать следующее для задачи выявления дефектных изделий среди общего количества изделий. ^[4] ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle d}$ ${\displaystyle n}$

1. Количество тестов, необходимых для асимптотически малой средней вероятности ошибки, масштабируется как . ${\displaystyle O(d\log _{2}n)}$
2. Количество тестов, необходимых для асимптотически малой максимальной вероятности ошибки, масштабируется как . ${\displaystyle O(d^{2}\log _{2}n)}$
3. Количество тестов, необходимых для нулевой вероятности ошибки, масштабируется как . ${\displaystyle O\left({\frac {d^{2}\log _{2}n}{\log _{2}d}}\right)}$

Обобщенный алгоритм двоичного разбиения

Иллюстрация обобщенного алгоритма бинарного разделения, где есть 8 дефектных и 135 всего элементов. Здесь, и первый тест дает отрицательный результат, поэтому каждый элемент объявляется бездефектным. Следовательно, осталось 119 элементов, поэтому . Эта вторая группа дает положительный результат, поэтому для поиска дефектного используется бинарный поиск. После этого весь процесс повторяется, вычисляя новый, используя только те элементы, дефектность которых не была определена. ${\displaystyle 2^{\alpha _{1}}=16}$ ${\displaystyle 2^{\alpha _{2}}=8}$ ${\displaystyle \alpha }$

Обобщенный алгоритм бинарного разделения представляет собой по сути оптимальный адаптивный алгоритм группового тестирования, который находит или уменьшает количество дефектных элементов следующим образом: ^{[3] [16]} ${\displaystyle d}$ ${\displaystyle n}$

1. Если , протестируйте элементы по отдельности. В противном случае установите и . ${\displaystyle n\leq 2d-2}$ ${\displaystyle n}$ ${\displaystyle l=n-d+1}$ ${\displaystyle \alpha =\lfloor \log _{2}{l/d}\rfloor }$
2. Протестируйте группу размером . Если результат отрицательный, каждый элемент в группе объявляется бездефектным; установите и перейдите к шагу 1. В противном случае используйте бинарный поиск , чтобы определить один дефектный и неопределенное количество, называемое , бездефектных элементов; установите и . Перейдите к шагу 1. ${\displaystyle 2^{\alpha }}$ ${\displaystyle n:=n-2^{\alpha }}$ ${\displaystyle x}$ ${\displaystyle n:=n-1-x}$ ${\displaystyle d:=d-1}$

Обобщенный алгоритм двоичного разделения требует не более чем тестов, где . ^[3] ${\displaystyle T}$ ${\displaystyle T={\begin{cases}n&n\leq 2d-2\\(\alpha +2)d+p-1&n\geq 2d-1\end{cases}}}$

Для больших можно показать, что , ^[3] что выгодно отличается от тестов, требуемых для алгоритма Ли -stage. Фактически, обобщенный алгоритм бинарного разбиения близок к оптимальному в следующем смысле. Когда можно показать, что , где - нижняя граница информации. ^{[3] [16]} ${\displaystyle n/d}$ ${\displaystyle T\rightarrow d\log _{2}(n/d)}$ ${\displaystyle t={\frac {e}{\log _{2}e}}d\log _{2}\left({\frac {n}{d}}\right)}$ ${\displaystyle s}$ ${\displaystyle d\geq 2}$ ${\displaystyle T-B_{I}(d,n)\leq (d-1)}$ ${\displaystyle B_{I}(d,n)=\left\lceil \log _{2}\sum _{i=0}^{d}{n \choose i}\right\rceil }$

Неадаптивные алгоритмы

Неадаптивные алгоритмы группового тестирования, как правило, предполагают, что число дефектных или, по крайней мере, их хорошая верхняя граница известны. ^[5] Это количество обозначено в этом разделе. Если границы неизвестны, существуют неадаптивные алгоритмы с низкой сложностью запроса, которые могут помочь оценить . ^[23] ${\displaystyle d}$ ${\displaystyle d}$

Комбинаторное ортогональное сопоставление (COMP)

Иллюстрация алгоритма COMP. COMP определяет элемент a как дефектный, а элемент b как недефектный. Однако он неверно маркирует c как дефектный, поскольку он «скрыт» дефектными элементами в каждом тесте, в котором он появляется.

Комбинаторный ортогональный поиск совпадений (COMP) — это простой неадаптивный алгоритм группового тестирования, который составляет основу более сложных алгоритмов, описанных в этом разделе.

Во-первых, каждая запись проверочной матрицы выбирается с вероятностью , а в противном случае — с вероятностью . ${\displaystyle 1}$ ${\displaystyle 1/d}$ ${\displaystyle 0}$

Шаг декодирования выполняется по столбцам (т. е. по элементам). Если каждый тест, в котором появляется элемент, положителен, то элемент объявляется дефектным; в противном случае элемент считается исправным. Или, что эквивалентно, если элемент появляется в любом тесте, результат которого отрицателен, элемент объявляется исправным; в противном случае элемент считается дефектным. Важным свойством этого алгоритма является то, что он никогда не создает ложных отрицательных результатов , хотя ложный положительный результат возникает, когда все местоположения с единицами в j -ом столбце (соответствующем исправному элементу j ) «скрыты» единицами других столбцов, соответствующих дефектным элементам. ${\displaystyle M}$

Алгоритм COMP требует не более тестов, чтобы вероятность ошибки была меньше или равна . ^[5] Это находится в пределах постоянного множителя нижней границы для средней вероятности ошибки выше. ${\displaystyle ed(1+\delta )\ln(n)}$ ${\displaystyle n^{-\delta }}$

В шумном случае ослабляется требование в исходном алгоритме COMP, чтобы набор расположений единиц в любом столбце, соответствующем положительному элементу, полностью содержался в наборе расположений единиц в результирующем векторе. Вместо этого допускается определенное количество «несовпадений» — это количество несовпадений зависит как от количества единиц в каждом столбце, так и от параметра шума, . Этот шумный алгоритм COMP требует не более тестов для достижения вероятности ошибки не более . ^[5] ${\displaystyle M}$ ${\displaystyle q}$ ${\displaystyle 4.36({\sqrt {\delta }}+{\sqrt {1+\delta }})^{2}(1-2q)^{-2}d\log _{2}{n}}$ ${\displaystyle n^{-\delta }}$

Определенно дефектные (DD)

Метод определенных дефектов (DD) является расширением алгоритма COMP, который пытается удалить любые ложные срабатывания. Было показано, что гарантии производительности для DD строго превышают гарантии COMP. ^[21]

Шаг декодирования использует полезное свойство алгоритма COMP: каждый элемент, который COMP объявляет недефектным, определенно недефектен (то есть нет ложных отрицательных результатов). Он действует следующим образом.

1. Сначала запускается алгоритм COMP, и любые недефектные элементы, которые он обнаруживает, удаляются. Все оставшиеся элементы теперь «возможно дефектные».
2. Далее алгоритм просматривает все положительные тесты. Если элемент появляется как единственный «возможный дефектный» в тесте, то он должен быть дефектным, поэтому алгоритм объявляет его дефектным.
3. Все остальные элементы предполагаются бездефектными. Обоснование этого последнего шага исходит из предположения, что количество дефектных элементов намного меньше общего количества элементов.

Обратите внимание, что шаги 1 и 2 никогда не делают ошибку, поэтому алгоритм может сделать ошибку только в том случае, если он объявляет дефектный элемент недефектным. Таким образом, алгоритм DD может создавать только ложные отрицательные результаты.

Последовательный COMP (SCOMP)

SCOMP (Sequential COMP) — это алгоритм, который использует тот факт, что DD не делает ошибок до последнего шага, где предполагается, что оставшиеся элементы не являются дефектными. Пусть набор заявленных дефектных элементов будет . Положительный тест называется объясненным , если он содержит хотя бы один элемент в . Ключевое наблюдение относительно SCOMP заключается в том, что набор дефектных элементов, обнаруженных DD, может не объяснять каждый положительный тест, и что каждый необъясненный тест должен содержать скрытый дефектный элемент. ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle K}$

Алгоритм работает следующим образом.

1. Выполните шаги 1 и 2 алгоритма DD , чтобы получить начальную оценку для набора дефектных изделий. ${\displaystyle K}$
2. Если объясняет каждый положительный тест, завершить алгоритм: это окончательная оценка для набора дефектных. ${\displaystyle K}$ ${\displaystyle K}$
3. Если есть какие-либо необъясненные тесты, найдите «возможный дефектный», который появляется в наибольшем количестве необъясненных тестов, и объявите его дефектным (то есть добавьте его в набор ). Перейдите к шагу 2. ${\displaystyle K}$

В ходе моделирования было показано, что SCOMP работает практически оптимально. ^[21]

Полиномиальные пулы (PP)

Детерминированный алгоритм, который гарантированно точно идентифицирует вплоть до положительных значений, — это полиномиальные пулы (PP). . ^[24] Алгоритм предназначен для построения матрицы объединения , которую можно напрямую использовать для декодирования наблюдений в . Подобно COMP, выборка декодируется в соответствии с соотношением: , где представляет собой поэлементное умножение, а — й столбец . Поскольку шаг декодирования несложный, PP специализируется на генерации . ${\displaystyle d}$ ${\displaystyle M}$ ${\displaystyle y}$ ${\displaystyle x_{i}=1~~{\text{ if }}~~M(:,i)~.*~y=M(:,i)}$ ${\displaystyle .*}$ ${\displaystyle M(:,i)}$ ${\displaystyle i}$ ${\displaystyle M}$ ${\displaystyle M}$

Формирование групп

Проектирование группы с образцами (синего цвета) из набора общих образцов с использованием алгоритма полиномиальных пулов ${\displaystyle q^{c-1}=9}$ ${\displaystyle n=q^{c}=27}$

Группа/пул генерируется с использованием полиномиального отношения, которое определяет индексы образцов, содержащихся в каждом пуле. Набор входных параметров определяет алгоритм. Для простого числа и целого числа любая степень простого числа определяется как . Для параметра размерности общее количество образцов равно , а количество образцов на пул равно . Кроме того, конечное поле порядка обозначается как (т. е. целые числа, определяемые специальными арифметическими операциями, которые гарантируют, что сложение и умножение в остается в ). Метод размещает каждый образец в сетке и представляет его координатами . Координаты вычисляются в соответствии с полиномиальным отношением с использованием целых чисел , ${\displaystyle \ell }$ ${\displaystyle p>1}$ ${\displaystyle n\geq 1}$ ${\displaystyle q=p^{n}}$ ${\displaystyle c\geq 2}$ ${\displaystyle n=q^{c}}$ ${\displaystyle q^{c-1}}$ ${\displaystyle q}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \{0,1,2,\ldots ,q-1\}}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle x=(u,v)}$ ${\displaystyle 1\leq l\leq c-1}$ ${\displaystyle 0\leq u_{i_{l}}\leq q-1}$

${\displaystyle v~=~a^{c-1}~u_{i_{c-1}}+\cdots +a~u_{i_{1}}+b,\quad a,b,u_{i_{l}}\in \mathbb {F} _{q}.}$

Комбинация циклов по значениям представлена ​​набором с элементами последовательности целых чисел, т. е. , где . Без потери общности комбинация такова, что циклы каждый раз, циклы каждый раз до циклы только один раз. Формулы, вычисляющие индексы выборки и, таким образом, соответствующие пулы для фиксированного и , задаются как ${\displaystyle u_{i_{l}}}$ ${\displaystyle q^{c-1}}$ ${\displaystyle d-1}$ ${\displaystyle u_{i_{1}}\times \cdots \times u_{i_{c-1}}=\{(i_{1},\ldots ,i_{c-1})\}}$ ${\displaystyle 0\leq i_{l}\leq q-1}$ ${\displaystyle i_{d-1}}$ ${\displaystyle q}$ ${\displaystyle i_{d-2}}$ ${\displaystyle q^{2}}$ ${\displaystyle i_{1}}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle {\begin{aligned}u_{i}&=\sum _{l=1}^{c-1}~q^{d-1-l}~i_{l}\\v_{u_{i}}&=\sum _{l=1}^{c-1}~a^{l}~i_{l}+b\quad ({\text{computed in }}\mathbb {F} _{q})\\x_{qu_{i}+v_{u_{i}}}&=(u_{i},v_{u_{i}})\end{aligned}}}$

Вычисления в можно реализовать с помощью общедоступных библиотек программного обеспечения для конечных полей, когда — степень простого числа. Когда — простое число, то вычисления в упрощаются до модульной арифметики, т. е . Пример того, как сгенерировать один пул , когда показан в таблице ниже, а соответствующий выбор образцов показан на рисунке выше. ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle v_{u_{i}}=(\sum _{l=1}^{c-1}a^{l}i_{l}+b)~{\text{mod}}~q}$ ${\displaystyle \ell }$ ${\displaystyle a=1,b=0,c=2}$

Этот метод использует тесты для точного определения до положительных результатов среди образцов. Из-за этого PP особенно эффективен для больших размеров выборки, поскольку количество тестов растет только линейно по отношению к , в то время как выборки растут экспоненциально с этим параметром. Однако PP может быть эффективен и для небольших размеров выборки. ^[24] ${\displaystyle q(c-1)(d+1)}$ ${\displaystyle d}$ ${\displaystyle n=q^{c}}$ ${\displaystyle c}$

Примеры приложений

Общность теории группового тестирования позволяет использовать ее во многих разнообразных приложениях, включая скрининг клонов, обнаружение коротких замыканий; ^[3] высокоскоростные компьютерные сети; ^[25] медицинское обследование, количественный поиск, статистику; ^[18] машинное обучение, секвенирование ДНК; ^[26] криптографию; ^{[27] [28]} и криминалистику данных. ^[29] В этом разделе представлен краткий обзор небольшой выборки этих приложений.

Каналы множественного доступа

Иллюстрация канала множественного доступа, показывающая успешное сообщение и столкновение сообщений

Канал множественного доступа — это канал связи, который соединяет множество пользователей одновременно. Каждый пользователь может слушать и передавать по каналу, но если одновременно передают более одного пользователя, сигналы сталкиваются и сводятся к неразборчивому шуму. Каналы множественного доступа важны для различных приложений реального мира, в частности, беспроводных компьютерных сетей и телефонных сетей. ^[30]

Одной из важных проблем с каналами множественного доступа является назначение пользователям времени передачи, чтобы их сообщения не сталкивались. Простой метод — предоставить каждому пользователю свой собственный временной интервал для передачи, требующий слотов. (Это называется мультиплексированием с временным разделением , или TDM.) Однако это очень неэффективно, поскольку назначает слоты передачи пользователям, у которых может не быть сообщения, и обычно предполагается, что только несколько пользователей захотят передавать в любой момент времени — в противном случае канал множественного доступа изначально непрактичен. ${\displaystyle n}$

В контексте группового тестирования эта проблема обычно решается путем деления времени на «эпохи» следующим образом. ^[3] Пользователь называется «активным», если у него есть сообщение в начале эпохи. (Если сообщение генерируется в течение эпохи, пользователь становится активным только в начале следующей.) Эпоха заканчивается, когда каждый активный пользователь успешно передал свое сообщение. Затем проблема заключается в том, чтобы найти всех активных пользователей в данной эпохе и запланировать время для них для передачи (если они еще не сделали этого успешно). Здесь тест на наборе пользователей соответствует тем пользователям, которые пытаются передать. Результатами теста являются количество пользователей, которые пытались передать, и , соответствующие соответственно отсутствию активных пользователей, ровно одному активному пользователю (успешное сообщение) или более чем одному активному пользователю (коллизия сообщений). Таким образом, используя адаптивный алгоритм группового тестирования с результатами , можно определить, какие пользователи хотят передать в эпоху. Затем любому пользователю, который еще не совершил успешную передачу, теперь можно назначить слот для передачи, не тратя время на неактивных пользователей. ${\displaystyle 0,1,}$ ${\displaystyle 2^{+}}$ ${\displaystyle \{0,1,2^{+}\}}$

Машинное обучение и сжатое зондирование

Машинное обучение — это область компьютерной науки, которая имеет множество программных приложений, таких как классификация ДНК, обнаружение мошенничества и целевая реклама. Одной из основных подобластей машинного обучения является проблема «обучения на примерах», где задача состоит в том, чтобы аппроксимировать некоторую неизвестную функцию, когда задано ее значение в ряде определенных точек. ^[3] Как указано в этом разделе, эта проблема обучения функции может быть решена с помощью подхода группового тестирования.

В простом варианте задачи есть некоторая неизвестная функция, где , и (используя логическую арифметику: сложение — это логическое ИЛИ, а умножение — это логическое И). Здесь ' разрежено', что означает, что в большинстве ее элементов . Цель состоит в том, чтобы построить приближение к использованию точечных оценок, где является как можно меньшим. ^[4] (Точное восстановление соответствует алгоритмам с нулевой ошибкой, тогда как аппроксимируется алгоритмами, которые имеют ненулевую вероятность ошибки.) ${\displaystyle f:\{0,1\}^{N}\to \{0,1\}}$ ${\displaystyle f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}}$ ${\displaystyle {\textbf {a}}\in \{0,1\}^{N}}$ ${\displaystyle {\textbf {a}}}$ ${\displaystyle d}$ ${\displaystyle d\ll N}$ ${\displaystyle 1}$ ${\displaystyle f}$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle f}$ ${\displaystyle f}$

В этой задаче восстановление эквивалентно нахождению . Более того, тогда и только тогда, когда существует некоторый индекс, , где . Таким образом, эта задача аналогична задаче группового тестирования с дефектными и общими элементами. Записи из являются элементами, которые дефектны, если они , задают тест, а тест положителен тогда и только тогда, когда . ^[4] ${\displaystyle f}$ ${\displaystyle {\textbf {a}}}$ ${\displaystyle f({\textbf {p}})=1}$ ${\displaystyle n}$ ${\displaystyle {\textbf {a}}_{n}={\textbf {p}}_{n}=1}$ ${\displaystyle d}$ ${\displaystyle n}$ ${\displaystyle {\textbf {a}}}$ ${\displaystyle 1}$ ${\displaystyle {\textbf {p}}}$ ${\displaystyle f({\textbf {p}})=1}$

В действительности, часто будут интересоваться более сложными функциями, такими как , снова где . Сжатое зондирование , которое тесно связано с групповым тестированием, может быть использовано для решения этой проблемы. ^[4] ${\displaystyle f:\mathbb {C} ^{N}\to \mathbb {C} }$ ${\displaystyle f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}}$

В сжатом измерении цель состоит в том, чтобы реконструировать сигнал, , путем проведения ряда измерений. Эти измерения моделируются как взятие скалярного произведения с выбранным вектором. ^[h] Цель состоит в том, чтобы использовать небольшое количество измерений, хотя это обычно невозможно, если не предположить что-то о сигнале. Одно из таких предположений (которое является общим ^{[33] [34]} ) заключается в том, что только небольшое количество записей являются значимыми , что означает, что они имеют большую величину. Поскольку измерения являются скалярными произведениями , справедливо уравнение , где — матрица, которая описывает набор выбранных измерений, а — набор результатов измерений. Эта конструкция показывает, что сжатое измерение — это своего рода «непрерывное» групповое тестирование. ${\displaystyle {\textbf {v}}\in \mathbb {C} ^{N}}$ ${\displaystyle {\textbf {v}}}$ ${\displaystyle {\textbf {v}}}$ ${\displaystyle {\textbf {v}}}$ ${\displaystyle M{\textbf {v}}={\textbf {q}}}$ ${\displaystyle M}$ ${\displaystyle t\times N}$ ${\displaystyle \mathbf {q} }$

Основная сложность сжатого зондирования заключается в определении того, какие записи являются значимыми. ^[33] После того, как это сделано, существует множество методов оценки фактических значений записей. ^[35] Эту задачу идентификации можно решить с помощью простого применения группового тестирования. Здесь групповой тест выдает комплексное число: сумму протестированных записей. Результат теста называется положительным, если он выдает комплексное число с большой величиной, что, учитывая предположение, что значимые записи разрежены, указывает на то, что по крайней мере одна значимая запись содержится в тесте.

Существуют явные детерминированные конструкции для этого типа алгоритма комбинаторного поиска, требующие измерений. ^[36] Однако, как и в случае с групповым тестированием, они не являются оптимальными, а случайные конструкции (такие как COMP) часто могут восстанавливаться сублинейно в . ^[35] ${\displaystyle d2^{(\log _{2}\log _{2}N)^{O(1)}}}$ ${\displaystyle f}$ ${\displaystyle N}$

Разработка мультиплексного анализа для тестирования COVID19

Во время пандемии, такой как вспышка COVID-19 в 2020 году, анализы на обнаружение вируса иногда проводятся с использованием неадаптивных схем группового тестирования. ^{[37] [38] [39]} Один из примеров был предоставлен проектом Origami Assays, который выпустил схемы группового тестирования с открытым исходным кодом для запуска на стандартном лабораторном 96-луночном планшете. ^[40]

Шаблон пробирной бумаги «Оригами» для группового тестирования

В лабораторных условиях одной из проблем группового тестирования является то, что создание смесей может быть трудоемким и сложным для точного выполнения вручную. Анализы оригами стали обходным путем для этой проблемы создания, предоставив бумажные шаблоны, чтобы помочь технику распределить образцы пациентов по тестовым лункам. ^[41]

Используя самые большие групповые тестовые проекты (XL3), можно было протестировать 1120 образцов пациентов в 94 аналитических лунках. Если истинно положительный процент был достаточно низким, то дополнительное тестирование не требовалось.

Криминалистическая экспертиза данных

Криминалистика данных — это область, посвященная поиску методов для сбора цифровых доказательств преступления. Такие преступления обычно связаны с тем, что злоумышленник изменяет данные, документы или базы данных жертвы, например, изменение налоговых записей, вирус, скрывающий свое присутствие, или вор личных данных, изменяющий персональные данные. ^[29]

Распространенным инструментом в криминалистике данных является односторонний криптографический хэш . Это функция, которая берет данные и с помощью труднообратимой процедуры создает уникальное число, называемое хешем. ^[i] Хэши, которые часто намного короче данных, позволяют нам проверять, были ли изменены данные, без необходимости расточительно хранить полные копии информации: хэш для текущих данных можно сравнить с прошлым хешем, чтобы определить, произошли ли какие-либо изменения. Неприятным свойством этого метода является то, что, хотя легко сказать, были ли данные изменены, нет способа определить, как: то есть невозможно восстановить, какая часть данных изменилась. ^[29]

Один из способов обойти это ограничение — хранить больше хэшей — теперь подмножеств структуры данных — чтобы сузить область, где произошла атака. Однако, чтобы найти точное место атаки с помощью наивного подхода, хэш должен быть сохранен для каждого элемента данных в структуре, что изначально сведет на нет смысл хэшей. (Можно также хранить обычную копию данных.) Групповое тестирование может использоваться для значительного сокращения количества хэшей, которые необходимо хранить. Тест становится сравнением между сохраненными и текущими хэшами, что является положительным, когда есть несоответствие. Это указывает на то, что по крайней мере один отредактированный элемент данных (который принимается за дефектность в этой модели) содержится в группе, которая сгенерировала текущий хэш. ^[29]

Фактически, количество необходимых хэшей настолько мало, что они, вместе с тестовой матрицей, на которую они ссылаются, могут даже храниться в организационной структуре самих данных. Это означает, что в отношении памяти тест может быть выполнен «бесплатно». (Это справедливо за исключением главного ключа/пароля, который используется для тайного определения функции хэширования.) ^[29]

Примечания

1. Первоначальная проблема, которую изучал Дорфман, была такого рода (хотя он не учитывал это), поскольку на практике только определенное количество сывороток крови могло быть объединено до того, как процедура тестирования становилась ненадежной. Это было главной причиной того, что процедура Дорфмана не применялась в то время. ^[3]
2. Однако, как это часто бывает в математике, групповое тестирование впоследствии было переизобретено несколько раз с тех пор, часто в контексте приложений. Например, Хейс независимо придумал идею опроса групп пользователей в контексте протоколов связи с множественным доступом в 1978 году. ^[9]
3. Иногда это называют гипотезой Ху-Хвана-Вана.
4. Количество тестов, , должно масштабироваться как для детерминированных планов, по сравнению с планами, которые допускают произвольно малые вероятности ошибок (как и ). ^[4] ${\displaystyle t}$ ${\displaystyle t=O\left(d^{2}\log _{d}n\right)}$ ${\displaystyle t=O(d\log _{2}n)}$ ${\displaystyle d\to \infty }$ ${\displaystyle n\to \infty }$
5. Необходимо быть внимательным, чтобы различать, когда тест сообщает о ложном результате, и когда процедура группового тестирования в целом терпит неудачу. Можно как сделать ошибку без неверных тестов, так и не сделать ошибку с некоторыми неверными тестами. Большинство современных комбинаторных алгоритмов имеют некоторую ненулевую вероятность ошибки (даже без ошибочных тестов), поскольку это значительно уменьшает количество необходимых тестов.
6. На самом деле можно сделать гораздо лучше. Например, алгоритм Ли на -этапе дает явное построение were . ${\displaystyle s}$ ${\displaystyle t\leq {\frac {e}{\log _{2}e}}d\log _{2}{(n/d)}}$
7. Альтернативно может быть определено уравнением , где умножение является логическим И ( ), а сложение является логическим ИЛИ ( ). Здесь, будет иметь в позиции тогда и только тогда, когда и оба являются для любого . То есть тогда и только тогда, когда по крайней мере один дефектный элемент был включен в тест. ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {y} :=M\mathbf {x} }$ ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle \mathbf {y} }$ ${\displaystyle 1}$ ${\displaystyle i}$ ${\displaystyle (M)_{i,j}}$ ${\displaystyle \mathbf {x} _{j}}$ ${\displaystyle 1}$ ${\displaystyle j}$ ${\displaystyle i{\textrm {-th}}}$
8. Этот тип измерений встречается во многих приложениях. Например, некоторые виды цифровых камер ^[31] или аппаратов МРТ ^[32] , где временные ограничения требуют, чтобы выполнялось лишь небольшое количество измерений.
9. Более формально хэши имеют свойство, называемое устойчивостью к коллизиям, которое заключается в том, что вероятность того, что один и тот же хэш будет получен из разных входов, очень мала для данных соответствующего размера. На практике вероятность того, что два разных входа могут создать один и тот же хэш, часто игнорируется.

Ссылки

Цитаты

1. Колборн, Чарльз Дж.; Диниц, Джеффри Х. (2007), Справочник по комбинаторным проектам (2-е изд.), Бока-Ратон: Chapman & Hall/CRC, стр. 574, Раздел 46: Объединенные проекты, ISBN 978-1-58488-506-1
2. Дорфман, Роберт (декабрь 1943 г.), «Обнаружение дефектных членов больших популяций», Анналы математической статистики , 14 (4): 436–440, doi : 10.1214/aoms/1177731363 , JSTOR  2235930
3. Дин-Чжу, Ду; Хванг, Фрэнк К. (1993). Комбинаторное групповое тестирование и его приложения . Сингапур: World Scientific. ISBN 978-9810212933.
4. Atia, George Kamal; Saligrama, Venkatesh (март 2012 г.). «Булево сжатое зондирование и шумное групповое тестирование». IEEE Transactions on Information Theory . 58 (3): 1880–1901. arXiv : 0907.1061 . doi :10.1109/TIT.2011.2178156. S2CID  8946216.
5. Chun Lam Chan; Pak Hou Che; Jaggi, Sidharth; Saligrama, Venkatesh (1 сентября 2011 г.). "Неадаптивное вероятностное групповое тестирование с зашумленными измерениями: почти оптимальные границы с эффективными алгоритмами". 49-я ежегодная конференция Allerton по коммуникациям, управлению и вычислениям . стр. 1832–9. arXiv : 1107.4540 . doi :10.1109/Allerton.2011.6120391. ISBN 978-1-4577-1817-5. S2CID  8408114.
6. Hung, M.; Swallow, William H. (март 1999). «Надежность группового тестирования при оценке пропорций». Биометрия . 55 (1): 231–7. doi :10.1111/j.0006-341X.1999.00231.x. PMID  11318160. S2CID  23389365.
7. Чэнь, Хун-Бин; Фу, Хун-Лин (апрель 2009 г.). «Неадаптивные алгоритмы для порогового группового тестирования». Дискретная прикладная математика . 157 (7): 1581–1585. doi : 10.1016/j.dam.2008.06.003 .
8. Де Бонис, Аннализа (20 июля 2007 г.). «Новые комбинаторные структуры с приложениями к эффективному групповому тестированию с ингибиторами». Журнал комбинаторной оптимизации . 15 (1): 77–94. doi :10.1007/s10878-007-9085-1. S2CID  207188798.
9. Хейс, Дж. (август 1978 г.). «Адаптивный метод локального распределения». Труды IEEE по коммуникациям . 26 (8): 1178–86. doi :10.1109/TCOM.1978.1094204.
10. Сэмюэлс, Стивен (1978). «Точное решение проблемы двухэтапного группового тестирования». Technometrics . 20 (4): 497–500. doi : 10.1080/00401706.1978.10489706 .
11. Стерретт, Эндрю (декабрь 1957 г.). «Об обнаружении дефектных членов больших популяций». Анналы математической статистики . 28 (4): 1033–6. doi : 10.1214/aoms/1177706807 .
12. Собель, Милтон; Гролл, Филлис А. (сентябрь 1959 г.). «Групповое тестирование для эффективного устранения всех дефектов в биномиальной выборке». Bell System Technical Journal . 38 (5): 1179–1252. doi :10.1002/j.1538-7305.1959.tb03914.x.
13. Унгар, Питер (февраль 1960 г.). «Точки отсечения в групповом тестировании». Сообщения по чистой и прикладной математике . 13 (1): 49–54. doi : 10.1002/cpa.3160130105 .
14. Ли, Чжоу Сюн (июнь 1962 г.). «Последовательный метод скрининга экспериментальных переменных». Журнал Американской статистической ассоциации . 57 (298): 455–477. doi :10.1080/01621459.1962.10480672.
15. Katona, Gyula OH (1973). «Обзор комбинаторной теории». Комбинаторные задачи поиска . Северная Голландия. С. 285–308. ISBN 978-0-7204-2262-7.
16. Hwang, Frank K. (сентябрь 1972 г.). «Метод обнаружения всех дефектных членов популяции путем группового тестирования». Журнал Американской статистической ассоциации . 67 (339): 605–608. doi :10.2307/2284447. JSTOR  2284447.
17. Аллеманн, Андреас (2013). "Эффективный алгоритм для комбинаторного группового тестирования". Теория информации, комбинаторика и теория поиска . Конспект лекций по информатике. Том 7777. С. 569–596. doi :10.1007/978-3-642-36899-8_29. ISBN 978-3-642-36898-1.
18. Hu, MC; Hwang, FK; Wang, Ju Kwei (июнь 1981 г.). «Граничное задание для группового тестирования». Журнал SIAM по алгебраическим и дискретным методам . 2 (2): 81–87. doi :10.1137/0602011.
19. Лей, Мин-Гуан (28 октября 2008 г.). «Заметка о гипотезе Ху–Хванга–Вана для группового тестирования». Журнал ANZIAM . 49 (4): 561. doi : 10.1017/S1446181108000175 .
20. Риччио, Лора; Колборн, Чарльз Дж. (1 января 2000 г.). «Более четкие границы в адаптивном групповом тестировании». Taiwanese Journal of Mathematics . 4 (4): 669–673. doi : 10.11650/twjm/1500407300 .
21. Олдридж, Мэтью; Балдассини, Леонардо; Джонсон, Оливер (июнь 2014 г.). «Алгоритмы группового тестирования: границы и симуляции». Труды IEEE по теории информации . 60 (6): 3671–3687. arXiv : 1306.6438 . doi : 10.1109/TIT.2014.2314472. S2CID  8885619.
22. Baldassini, L.; Johnson, O.; Aldridge, M. (1 июля 2013 г.), "2013 IEEE International Symposium on Information Theory", IEEE International Symposium on Information Theory , стр. 2676–2680, arXiv : 1301.7023 , CiteSeerX 10.1.1.768.8924 , doi : 10.1109/ISIT.2013.6620712, ISBN  978-1-4799-0446-4, S2CID  9987210
23. Собель, Милтон; Элашофф, Р. М. (1975). «Групповое тестирование с новой целью, оценка». Biometrika . 62 (1): 181–193. doi :10.1093/biomet/62.1.181. hdl : 11299/199154 ​​.
24. . «Эффективные матричные конструкции для группового тестирования COVID-19». BMC Bioinformatics . 24 (26): 26. doi : 10.1186/s12859-023-05145-y . PMC 9872308. PMID  36694117. 
25. Бар-Ной, А.; Хванг, ФК; Кесслер, И.; Куттен, С. (1 мая 1992 г.). «Новый конкурентный алгоритм для группового тестирования». [Труды] IEEE INFOCOM '92: Конференция по компьютерным коммуникациям . Том 2. стр. 786–793. doi :10.1109/INFCOM.1992.263516. ISBN 978-0-7803-0602-8. S2CID  16131063.
26. Дамашке, Питер (2000). «Адаптивное и неадаптивное обучение с эффективным использованием атрибутов». Машинное обучение . 41 (2): 197–215. doi : 10.1023/A:1007616604496 .
27. Стинсон, DR; ван Трунг, Тран; Вэй, Р. (май 2000 г.). «Безопасные коды с защитой от фреймов, шаблоны распределения ключей, алгоритмы группового тестирования и связанные структуры». Журнал статистического планирования и вывода . 86 (2): 595–617. CiteSeerX 10.1.1.54.6212 . doi :10.1016/S0378-3758(99)00131-7. 
28. Колборн, CJ; Диниц, JH; Стинсон, DR (1999). «Коммуникации, криптография и сети». Обзоры по комбинаторике . 3 (267): 37–41. doi : 10.1007/BF01609873 . S2CID  10128581.
29. Goodrich, Michael T.; Atallah, Michael J.; Tamassia, Roberto (2005). "Индексирование информации для криминалистики данных". Прикладная криптография и сетевая безопасность . Конспект лекций по информатике. Том 3531. С. 206–221. CiteSeerX 10.1.1.158.6036 . doi :10.1007/11496137_15. ISBN  978-3-540-26223-7.
30. Chlebus, BS (2001). «Рандомизированная связь в радиосетях». В Pardalos, PM; Rajasekaran, S.; Reif, J.; Rolim, JDP (ред.). Справочник по рандомизированным вычислениям . Kluwer Academic. стр. 401–456. ISBN 978-0-7923-6957-8.
31. Takhar, D.; Laska, JN; Wakin, MB; Duarte, MF; Baron, D.; Sarvotham, S.; Kelly, KF; Baraniuk, RG (февраль 2006 г.). Bouman, Charles A.; Miller, Eric L.; Pollak, Ilya (ред.). "Новая архитектура камеры сжатого изображения с использованием сжатия оптического домена". Electronic Imaging . Computational Imaging IV. 6065 : 606509–606509–10. Bibcode :2006SPIE.6065...43T. CiteSeerX 10.1.1.114.7872 . doi :10.1117/12.659602. S2CID  7513433. 
32. Кандес, Э. Дж. (2014). «Математика разреженности (и несколько других вещей)». Труды Международного конгресса математиков. Сеул, Южная Корея .
33. Gilbert, AC; Iwen, MA; Strauss, MJ (октябрь 2008 г.). "Групповое тестирование и восстановление разреженных сигналов". 42-я Асиломарская конференция по сигналам, системам и компьютерам . Институт инженеров по электротехнике и электронике. стр. 1059–63. doi :10.1109/ACSSC.2008.5074574. ISBN 978-1-4244-2940-0.
34. Райт, С. Дж.; Новак, Р. Д.; Фигейредо, М. А. Т. (июль 2009 г.). «Разреженная реконструкция с помощью разделяемой аппроксимации». Труды IEEE по обработке сигналов . 57 (7): 2479–2493. Bibcode : 2009ITSP...57.2479W. CiteSeerX 10.1.1.142.749 . doi : 10.1109/TSP.2009.2016892. S2CID  7399917. 
35. Berinde, R.; Gilbert, AC; Indyk, P.; Karloff, H.; Strauss, MJ (сентябрь 2008 г.). «Объединение геометрии и комбинаторики: единый подход к восстановлению разреженных сигналов». 2008 г. 46-я ежегодная конференция Allerton по коммуникациям, управлению и вычислениям . стр. 798–805. arXiv : 0804.4666 . doi :10.1109/ALLERTON.2008.4797639. ISBN 978-1-4244-2925-7. S2CID  8301134.
36. Индик, Петр (1 января 2008 г.). «Явные конструкции для сжатого считывания разреженных сигналов». Труды девятнадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам : 30–33.
37. Остин, Дэвид. «AMS Feature Column — Объединение стратегий для тестирования COVID-19». Американское математическое общество . Получено 2020-10-03 .
38. Прасанна, Дирадж. «Объединение гобеленов». Tapestry-pooling.herokuapp.com . Проверено 03 октября 2020 г.
39. Chiani, M.; Liva, G.; Paolini, E. (февраль 2022 г.), «Протоколы группового тестирования идентификации и обнаружения COVID-19 при высокой распространенности», Scientific Reports , 12 (1), Springer Nature: 3250, arXiv : 2104.11305 , Bibcode : 2022NatSR..12.3250C, doi : 10.1038/s41598-022-07205-4 , PMC 8885674 , PMID  35228579, S2CID  233387831 
40. "Origami Assays". Origami Assays. 2 апреля 2020 г. Получено 7 апреля 2020 г.
41. "Origami Assays". Origami Assays. 2 апреля 2020 г. Получено 7 апреля 2020 г.

Общие ссылки

• Дин-Чжу, Ду; Хван, Фрэнк К. (1993). Комбинаторное групповое тестирование и его приложения . Сингапур: World Scientific. ISBN 978-9810212933.
• Курс Атри Рудры «Коды с исправлением ошибок: комбинаторика, алгоритмы и приложения» (весна 2007 г.), лекции 7.
• Курс Атри Рудры «Коды с исправлением ошибок: комбинаторика, алгоритмы и приложения» (весна 2010 г.), лекции 10, 11, 28, 29
• Ду, Д.; Хванг, Ф. (2006). Объединение планов и неадаптивное групповое тестирование. World Scientific. ISBN 9789814477864.
• Олдридж, М.; Джонсон, О.; Скарлетт, Дж. (2019). «Групповое тестирование: перспектива теории информации» (PDF) . Основы и тенденции в теории коммуникаций и информации . 15 (3–4): 196–392. doi :10.1561/0100000099. S2CID  62841593.
• Porat, E.; Rothschild, A. (2011). «Явные неадаптивные комбинаторные схемы группового тестирования». IEEE Transactions on Information Theory . 57 (12): 7982–89. arXiv : 0712.3876 . doi : 10.1109/TIT.2011.2163296. S2CID  8815474.
• Каган, Юджин; Бен-гал, Ирад (2014), «Алгоритм группового тестирования с информационным обучением онлайн», IIE Transactions , 46 (2): 164–184, doi : 10.1080/0740817X.2013.803639, ISSN  0740-817X, S2CID  18588494

Смотрите также

• Головоломка на равновесие