R-четность

Дискретная симметрия в некоторых суперсимметричных моделях

R-четность — это концепция в физике элементарных частиц . В Минимальной Суперсимметричной Стандартной Модели барионное число и лептонное число больше не сохраняются всеми перенормируемыми связями в теории. Поскольку сохранение барионного числа и лептонного числа было проверено очень точно, эти связи должны быть очень малыми, чтобы не противоречить экспериментальным данным. R-четность — это симметрия, действующая на поля Минимальной Суперсимметричной Стандартной Модели (MSSM), которая запрещает эти связи и может быть определена как ^[1] ${\displaystyle \mathbb {Z} _{2}}$

${\displaystyle P_{\mathrm {R} }=(-1)^{3B+L+2s},}$

или, что то же самое, как

${\displaystyle P_{\mathrm {R} }=(-1)^{3(B-L)+2s},}$

где s — спин , B — барионное число, а L — лептонное число. Все частицы Стандартной модели имеют R-четность +1, тогда как суперсимметричные частицы имеют R-четность −1.

Обратите внимание, что существуют различные формы паритета с различными эффектами и принципами; не следует путать этот паритет с каким-либо другим паритетом .

Кандидат на темную материю

При сохранении R-четности самая легкая суперсимметричная частица ( LSP ) не может распасться. Эта самая легкая частица (если она существует) может, следовательно, отвечать за наблюдаемую недостающую массу Вселенной, которую обычно называют темной материей . ^[2] Для того, чтобы соответствовать наблюдениям, предполагается, что эта частица имеет массу100  ГэВ / c2 до1  ТэВ/ c ² , нейтрален и взаимодействует только посредством слабых взаимодействий и гравитационных взаимодействий . Его часто называют слабовзаимодействующей массивной частицей или WIMP.

Обычно кандидат на темную материю MSSM представляет собой смесь электрослабых гейджино и хиггсино и называется нейтралино . В расширениях MSSM возможно, что кандидатом на темную материю будет снейтрино . Другая возможность — гравитино , которое взаимодействует только посредством гравитационных взаимодействий и не требует строгой R-четности.

Связи MSSM, нарушающие R-четность

Перенормируемые связи, нарушающие R-четность, в MSSM следующие:

• ${\displaystyle \int d^{2}\theta \;\lambda _{1}\;U^{c}D^{c}D^{c}}$нарушает B на 1 единицу

Самое сильное ограничение, связанное только с этой связью, возникает из-за отсутствия наблюдения нейтрон-антинейтронных осцилляций.

• ${\displaystyle \int d^{2}\theta \;\lambda _{2}\;QD^{c}L}$нарушает L на 1 единицу

Самым сильным ограничением, связанным только с этой связью, является нарушение универсальности константы Ферми в распадах кварков и лептонных заряженных токов. ${\displaystyle G_{F}}$

• ${\displaystyle \int d^{2}\theta \;\lambda _{3}\;LE^{c}L}$нарушает L на 1 единицу

Самым сильным ограничением, связанным только с этой связью, является нарушение универсальности константы Ферми в распадах лептонных заряженных токов.

• ${\displaystyle \int d^{2}\theta \;\kappa \;LH_{u}}$нарушает L на 1 единицу

Самым сильным ограничением, связанным с этой связью, является то, что она приводит к большой массе нейтрино.

Хотя ограничения на отдельные связи достаточно сильны, если объединить несколько связей, они приведут к распаду протона . Таким образом, существуют дополнительные максимальные ограничения на значения связей из максимальных ограничений на скорость распада протона.

Распад протона

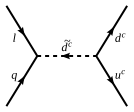
Без сохранения барионного и лептонного числа и учета связей для связей, нарушающих R-четность, протон может распасться примерно за 10−2 ^секунд или, если предположить минимальное нарушение аромата, время жизни протона может быть увеличено до 1 года. Поскольку, как наблюдалось, время жизни протона превышает 1033–1034 ^лет  ( ^в  зависимости от точного канала распада), это сильно невыгодно для модели. R-четность устанавливает все перенормируемые связи, нарушающие барионное и лептонное число, равными нулю, и протон стабилен на перенормируемом уровне, а время жизни протона увеличивается до 1032 ^лет  и почти согласуется с текущими данными наблюдений. ${\displaystyle {\mathcal {O}}(1)}$

Поскольку распад протона включает в себя нарушение как лептонного, так и барионного числа одновременно, ни одна перенормируемая связь, нарушающая R-четность, не приводит к распаду протона. Это побудило к изучению нарушения R-четности, когда только один набор связей, нарушающих R-четность, не равен нулю, что иногда называют гипотезой доминирования одиночной связи.

Возможные истоки R-четности

Очень привлекательным способом мотивации R-четности является непрерывная калибровочная симметрия B − L , которая спонтанно нарушается в масштабе, недоступном для текущих экспериментов. Непрерывность запрещает перенормируемые члены, которые нарушают B и L. ^{[3] [4] [5] [6]} Если нарушается только скалярными вакуумными ожидаемыми значениями (или другими параметрами порядка), которые несут четные целые значения 3( B − L ) , то существует точно сохраняющаяся дискретная остаточная подгруппа, которая обладает желаемыми свойствами. ^{[7] [8] [9] [10] [11]} Ключевой вопрос заключается в том, чтобы определить, развивает ли снейтрино (суперсимметричный партнер нейтрино), который является нечетным относительно R-четности, вакуумное ожидаемое значение. Можно показать, на феноменологических основаниях, что это не может произойти ни в какой теории, где нарушается в масштабе, намного превышающем электрослабый . Это верно в любой теории, основанной на крупномасштабном механизме качелей . ^[12] Как следствие, в таких теориях R-четность остается точной при всех энергиях. ${\displaystyle U(1)_{B-L}}$ ${\displaystyle U(1)_{B-L}}$ ${\displaystyle U(1)_{B-L}}$

Это явление может возникнуть как автоматическая симметрия в теориях великого объединения SO(10) . Это естественное возникновение R-четности возможно, потому что в SO(10) фермионы Стандартной модели возникают из 16-мерного спинорного представления , в то время как Хиггс возникает из 10-мерного векторного представления. Для того чтобы создать инвариантную связь SO(10), необходимо иметь четное число спинорных полей (т. е. должна быть спинорная четность). После нарушения симметрии GUT эта спинорная четность спускается в R-четность, если только спинорные поля не использовались для нарушения симметрии GUT. Были построены явные примеры таких теорий SO(10). ^{[13] [14]}

Смотрите также

• R-симметрия

Ссылки

1. Мартин, СП (6 сентября 2011 г.). "A Supersymmetry Primer". Расширенная серия по направлениям в физике высоких энергий . 18 : 1–98. arXiv : hep-ph/9709356 . doi :10.1142/9789812839657_0001. ISBN 978-981-02-3553-6. S2CID  118973381.
2. Юнгман, Г.; Камионковски, М.; Грист, К. (1996). «Суперсимметричная темная материя». Physics Reports . 267 (5–6): 195–373. arXiv : hep-ph/9506380 . Bibcode : 1996PhR...267..195J. doi : 10.1016/0370-1573(95)00058-5. S2CID  119067698.
3. Mohapatra, RN (1986). «Новые вклады в безнейтринный двойной бета-распад в суперсимметричных теориях». Physical Review D. 34 ( 11): 3457–3461. Bibcode : 1986PhRvD..34.3457M. doi : 10.1103/PhysRevD.34.3457. PMID  9957083.
4. Фонт, А.; Ибаньес, Л.Е.; Кеведо, Ф. (1989). «Означает ли стабильность протона существование дополнительного Z0?» (PDF) . Physics Letters B. 228 ( 1): 79–88. Bibcode : 1989PhLB..228...79F. doi : 10.1016/0370-2693(89)90529-7.
5. Мартин, СП (1992). «Некоторые простые критерии для калиброванной R-четности». Physical Review D. 46 ( 7): R2769–R2772. arXiv : hep-ph/9207218 . Bibcode : 1992PhRvD..46.2769M. doi : 10.1103/PhysRevD.46.R2769. PMID  10015267. S2CID  14821065.
6. Мартин, СП (1996). «Следствия суперсимметричных моделей с естественным сохранением R-четности». Physical Review D. 54 ( 3): 2340–2348. arXiv : hep-ph/9602349 . Bibcode : 1996PhRvD..54.2340M. doi : 10.1103/PhysRevD.54.2340. PMID  10020912. S2CID  5751474.
7. Fayet, P. (1975). «Суперкалибровочно-инвариантное расширение механизма Хиггса и модель для электрона и его нейтрино». Nuclear Physics B. 90 : 104–124. Bibcode : 1975NuPhB..90..104F. doi : 10.1016/0550-3213(75)90636-7.
8. Салам, А.; Стратди, Дж. (1975). «Суперсимметрия и сохранение числа фермионов». Nuclear Physics B. 87 ( 1): 85–92. Bibcode : 1975NuPhB..87...85S. doi : 10.1016/0550-3213(75)90253-9.
9. Фаррар, GR; Вайнберг, S. (1983). "Суперсимметрия при обычных энергиях. II. R-инвариантность, бозоны Голдстоуна и массы калибровочных фермионов". Physical Review D. 27 ( 11): 2732. Bibcode : 1983PhRvD..27.2732F. doi : 10.1103/PhysRevD.27.2732.
10. Fayet, P. (1977). «Спонтанно нарушенные суперсимметричные теории слабых, электромагнитных и сильных взаимодействий». Physics Letters B. 69 ( 4): 489–494. Bibcode : 1977PhLB...69..489F. doi : 10.1016/0370-2693(77)90852-8.
11. Фаррар, GR; Файет, П. (1978). «Феноменология образования, распада и обнаружения новых адронных состояний, связанных с суперсимметрией». Physics Letters B. 76 ( 5): 575. Bibcode : 1978PhLB...76..575F. doi : 10.1016/0370-2693(78)90858-4.
12. Aulakh, CS; Melfo, A.; Rašin, A.; Senjanović, G. (1998). "Суперсимметрия и крупномасштабная лево-правая симметрия". Physical Review D. 58 ( 11): 115007. arXiv : hep-ph/9712551 . Bibcode : 1998PhRvD..58k5007A. doi : 10.1103/PhysRevD.58.115007. S2CID  43296921.
13. Aulakh, CS; Bajc, B.; Melfo, A.; Rašin, A.; Senjanović, G. (2001). "SO(10) теория R-четности и масса нейтрино". Nuclear Physics B . 597 (1–3): 89–109. arXiv : hep-ph/0004031 . Bibcode :2001NuPhB.597...89A. doi :10.1016/S0550-3213(00)00721-5. S2CID  119100803.
14. Aulakh, CS; Bajc, B.; Melfo, A.; Senjanović, G.; Vissani, F. (2004). «Минимальная суперсимметричная теория великого объединения». Physics Letters B. 588 ( 3–4): 196–202. arXiv : hep-ph/0306242 . Bibcode : 2004PhLB..588..196A. doi : 10.1016/j.physletb.2004.03.031. S2CID  119401374.

Внешние ссылки

• Барбье, Р.; и др. (2005). «Нарушающая R-четность суперсимметрия». Physics Reports . 420 (1–6): 1–195. arXiv : hep-ph/0406039 . Bibcode : 2005PhR...420....1B. doi : 10.1016/j.physrep.2005.08.006.
• «Нарушение R-четности ...» xstructure.inr.ac.ru .
• "Нарушение R-четности ..." FNAL . Архивировано из оригинала 2010-05-28.