Резисторная лестница представляет собой электрическую цепь, состоящую из повторяющихся блоков резисторов в определенных конфигурациях.
Конфигурация лестничной цепи R–2R представляет собой простой и недорогой способ выполнения цифро-аналогового преобразования (ЦАП) с использованием повторяющихся расположений точных резисторных цепей в лестничной конфигурации.
В статье 1953 года «Кодирование методами обратной связи» [1] описываются «декодирующие сети», которые преобразуют числа (в любой базе ), представленные источниками напряжения или источниками тока, подключенными к резистивным сетям в «декодирующей сети шунтирующего резистора» (которая в базе 2 соответствует двоично-взвешенной конфигурации) или в «декодирующей сети лестничного резистора» (которая в базе 2 соответствует конфигурации R–2R) в один выход напряжения. В статье приводится преимущество R–2R в том, что импедансы , видимые источниками, более равны.
Другое историческое описание содержится в патенте США 3108266, поданном в 1955 году, «Устройство преобразования сигналов» [2] .
Цепочка из множества резисторов, подключенных между двумя опорными напряжениями, называется «цепочкой резисторов». Резисторы действуют как делители напряжения между опорными напряжениями. Делитель Кельвина или строковый ЦАП представляет собой цепочку резисторов одинакового номинала. [3]
Каждое нажатие на строку генерирует разное напряжение, которое можно сравнить с другим напряжением: это основной принцип работы флэш-АЦП (аналого-цифрового преобразователя). Главным недостатком является то, что эта архитектура требует компараторов, по одному на каждый резистор; и это число нельзя уменьшить, используя сеть R-2R, поскольку такая сеть не будет иметь отдельных выходов для каждого напряжения.
Цепочка резисторов может функционировать как ЦАП, имея биты двоичного числа, управляющие электронными переключателями, подключенными к каждому отводу. [4]
Двоичная взвешенная конфигурация использует мощность двух кратных базового значения резистора. Однако, по мере увеличения соотношений значений резисторов, способность подгонять резисторы к точным допускам соотношений уменьшается. Более точные соотношения могут быть получены при использовании аналогичных значений, как это используется в лестнице R–2R. Следовательно, R–2R обеспечивает более точное цифро-аналоговое преобразование. [5] [6]

Режим напряжения R–2R резисторной лестничной сети показан на рисунке 1. Биты a n −1 (старший значащий бит, MSB) через бит a 0 (младший значащий бит, LSB) управляются цифровыми логическими вентилями. В идеале битовые входы переключаются между V = 0 (логический 0) и V = V ref (логическая 1). Сеть R–2R заставляет эти цифровые биты взвешиваться в их вкладе в выходное напряжение V out . В зависимости от того, какие биты установлены в 1, а какие в 0, выходное напряжение ( V out ) будет иметь соответствующее ступенчатое значение между 0 и V ref минус значение минимального шага, соответствующего биту 0. Фактическое значение V ref (и напряжение логического 0) будет зависеть от типа технологии, используемой для генерации цифровых сигналов. [7]
Для цифрового значения VAL ЦАП R–2R с N битами и логическими уровнями 0 В/ V опорного напряжения выходное напряжение V вых равно:
Например, если N = 5 (следовательно, 2 N = 32) и V ref = 3,3 В (типичное напряжение логики 1 КМОП), то V out будет изменяться от 0 вольт (VAL = 0 = 00000 2 ) до максимума (VAL = 31 = 11111 2 ):
с шагами (соответствующими VAL = 1 = 00001 2 )
Лестница R–2R недорога и относительно проста в изготовлении, поскольку требуются только два значения резистора (или даже одно, если R выполнен путем размещения пары 2R параллельно, или если 2R выполнен путем размещения пары R последовательно). Она быстрая и имеет фиксированное выходное сопротивление R. Лестница R–2R работает как цепочка делителей тока , точность выходного сигнала которой зависит исключительно от того, насколько хорошо каждый резистор согласован с другими. Небольшие неточности в резисторах MSB могут полностью подавить вклад резисторов LSB. Это может привести к немонотонному поведению на основных переходах, например, от 01111 2 до 10000 2 .
В зависимости от типа используемых логических вентилей и конструкции логических схем, могут быть переходные всплески напряжения на таких крупных перекрестках даже при идеальных значениях резисторов. Они могут быть отфильтрованы с помощью емкости на выходном узле (последующее уменьшение полосы пропускания может быть значительным в некоторых приложениях). Наконец, сопротивление 2R последовательно с цифровым выходным импедансом. Вентили с высоким выходным импедансом (например, LVDS ) могут быть непригодны в некоторых случаях. По всем вышеперечисленным причинам (и, несомненно, другим) этот тип ЦАП имеет тенденцию ограничиваться относительно небольшим числом бит; хотя интегральные схемы могут увеличить число бит до 14 или даже больше, 8 бит или меньше является более типичным.
Описанный выше ЦАП R–2R напрямую выдает напряжение и поэтому называется режимом напряжения (или иногда нормальным режимом ).
Поскольку выходное сопротивление не зависит от цифрового кода, аналоговый выход может быть с тем же успехом принят за ток в виртуальную землю, конфигурация, называемая токовым режимом (или иногда инвертированным режимом ). Используя токовое состояние , усиление ЦАП может быть отрегулировано последовательным резистором на клемме опорного напряжения. [8] Ток для всех битов проходит через эквивалентное сопротивление 2R относительно земли. Чем менее значим бит, тем больше резисторов должен пройти его сигнал. В каждом узле ток каждого бита делится на два. [9]
Резисторы, используемые с более значимыми битами, должны быть пропорционально точнее, чем те, которые используются с менее значимыми битами; например, в сети R–2R, обсуждавшейся выше, неточности в резисторах бита-4 (MSB) должны быть незначительными по сравнению с 1 ⁄ 32 (~3,1%) от R. Кроме того, чтобы избежать проблем при переходе от 10000 2 к 01111 2 , сумма неточностей в младших битах также должна быть значительно меньше этой. Требуемая точность удваивается с каждым дополнительным битом: для 8 бит требуемая точность будет лучше, чем 1 ⁄ 256 (~0,4%). [ необходимо разъяснение ]
Однако отклонения сопротивлений при изготовлении в виде одного компонента, как правило, намного ниже отклонений между компонентами или между партиями производства, и, следовательно, резисторную сеть можно приобрести как один компонент. А в интегральных схемах высокоточные сети R–2R можно печатать непосредственно на одной подложке с использованием тонкопленочной технологии, гарантируя, что резисторы имеют схожие электрические характеристики. Тем не менее, их часто приходится подрезать лазером для достижения требуемой точности. Были продемонстрированы такие встроенные в чип резисторные лестницы для цифро-аналоговых преобразователей, достигающие 16-битной точности. [10]
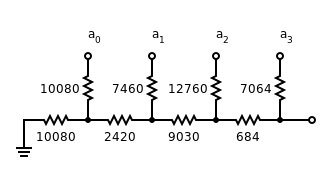
Не обязательно, чтобы каждая «ступенька» лестницы R–2R использовала одинаковые значения резисторов. Необходимо только, чтобы значение «2R» совпадало с суммой значения «R» плюс эквивалентное сопротивление Тевенина ступеней с меньшей значимостью. На рисунке 2 показан линейный 4-битный ЦАП с неравными резисторами.
Это позволяет создать достаточно точный ЦАП из разнородного набора резисторов, формируя ЦАП по одному биту за раз. На каждом этапе резисторы для «ступени» и «ноги» выбираются так, чтобы значение ступени соответствовало значению ноги плюс эквивалентное сопротивление предыдущих ступеней. Резисторы ступени и ноги могут быть сформированы путем последовательного или параллельного соединения других резисторов для увеличения количества доступных комбинаций. Этот процесс можно автоматизировать.