Масштабированная корреляция

В статистике масштабированная корреляция — это форма коэффициента корреляции, применимая к данным, имеющим временную составляющую , таким как временные ряды . Это средняя краткосрочная корреляция. Если сигналы имеют несколько компонентов (медленные и быстрые), масштабированный коэффициент корреляции можно вычислить только для быстрых компонентов сигналов, игнорируя вклад медленных компонентов. ^[1] Эта операция , подобная фильтрации, имеет то преимущество, что не нужно делать предположений о синусоидальной природе сигналов.

Например, при изучении сигналов мозга исследователи часто интересуются высокочастотными компонентами (бета- и гамма-диапазон; 25–80 Гц) и могут не интересоваться низкочастотными диапазонами (альфа, тета и т. д.). В этом случае масштабированную корреляцию можно вычислить только для частот выше 25 Гц, выбрав масштаб анализа s , соответствующий периоду этой частоты (например, s  = 40 мс для колебаний 25 Гц).

Определение

Масштабированная корреляция между двумя сигналами определяется как средняя корреляция, вычисленная по коротким сегментам этих сигналов. Во-первых, необходимо определить количество сегментов , которые могут вписаться в общую длину сигналов для данного масштаба : ${\displaystyle K}$ ${\displaystyle T}$ ${\displaystyle s}$

${\displaystyle K=\operatorname {round} \left({\frac {T}{s}}\right).}$

Далее, если — коэффициент корреляции Пирсона для сегмента , то масштабированная корреляция по всем сигналам вычисляется как ${\displaystyle r_{k}}$ ${\displaystyle k}$ ${\displaystyle {\bar {r}}_{s}}$

${\displaystyle {\bar {r}}_{s}={\frac {1}{K}}\sum \limits _{k=1}^{K}r_{k}.}$

Эффективность

В подробном анализе Николич и др. ^[1] показали, что степень ослабления вкладов медленных компонентов зависит от трех факторов: выбора масштаба, соотношения амплитуд между медленным и быстрым компонентом и различий в частотах их колебаний. Чем больше различия в частотах колебаний, тем эффективнее будут удаляться вклады медленных компонентов из вычисляемого коэффициента корреляции. Аналогично, чем меньше мощность медленных компонентов по сравнению с быстрыми компонентами, тем лучше будет работать масштабированная корреляция.

Применение к кросс-корреляции

Пример кросс-коррелограммы между последовательностями спайков, вычисленными классическим способом (слева) и с использованием масштабированной корреляции (справа; = 200 мс). Масштабированная корреляция удаляет медленный компонент из кросс-коррелограммы. ${\displaystyle s}$

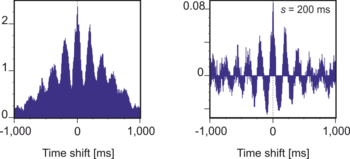
Масштабированную корреляцию можно применять к авто- и кросс-корреляции , чтобы исследовать, как корреляции высокочастотных компонентов изменяются при разных временных задержках. Чтобы правильно вычислить кросс-масштабированную корреляцию для каждого временного сдвига, необходимо заново сегментировать сигналы после каждого временного сдвига. Другими словами, сигналы всегда смещаются до применения сегментации. Масштабированная корреляция впоследствии использовалась для исследования синхронизирующих концентраторов в зрительной коре. ^[2] Масштабированная корреляция также может использоваться для извлечения функциональных сетей. ^[3]

Преимущества перед методами фильтрации

Масштабированная корреляция во многих случаях должна быть предпочтительнее фильтрации сигнала на основе спектральных методов. Преимущество масштабированной корреляции заключается в том, что она не делает предположений о спектральных свойствах сигнала (например, синусоидальной форме сигналов). Николич и др. ^[1] показали, что использование теоремы Винера–Хинчина для удаления медленных компонентов уступает результатам, полученным с помощью масштабированной корреляции. Эти преимущества становятся очевидными, особенно когда сигналы непериодичны или состоят из дискретных событий, таких как временные метки, в которых были обнаружены потенциалы действия нейронов.

Связанные методы

Детальное представление о структуре корреляции в различных масштабах может быть получено путем визуализации с использованием многомасштабного корреляционного анализа. ^[4]

Смотрите также

• Автокорреляция
• Когерентность (обработка сигнала)
• Свертка
• Корреляция
• Кросс-корреляция
• Фазовая корреляция
• Спектральная плотность
• Кросс-спектр
• Теорема Винера–Хинчина

Ссылки

1. Николич Д., Муресан Р. К., Фенг В., Сингер В. (2012) Анализ масштабированной корреляции: лучший способ вычисления кросс-коррелограммы. Европейский журнал нейронауки , стр. 1–21, doi:10.1111/j.1460-9568.2011.07987.x http://www.danko-nikolic.com/wp-content/uploads/2012/03/Scaled-correlation-analysis.pdf
2. Фолиас, С. Э., С. Ю., А. Снайдер, Д. Николич и Дж. Э. Рубин (2013) Синхронизирующие узлы в зрительной коре могут возникать из-за сильного ритмического торможения во время гамма-колебаний. Европейский журнал нейронауки , 38(6): 2864–2883.
3. Dolean, S., Dînşoreanu, M., Mureşan, RC, Geiszt, A., Potolea, R., & Ţincaş, I. (2017, сентябрь). Подход на основе масштабированной корреляции для определения и анализа функциональных сетей. В Международном семинаре по новым рубежам в горнодобывающих сложных моделях (стр. 80–92). Springer, Cham.
4. Пасанен, Л. и Хольмстрём, Л. (2016). «Анализ корреляции с множественным разрешением в масштабном пространстве для данных временных рядов». Computational Statistics , 1–22.

Бесплатные источники

• Бесплатный исходный код для вычисления масштабированной взаимной корреляции и интерфейс для MATLAB можно загрузить здесь: http://www.raulmuresan.ro/sources/corrlib/
• Простой демонстрационный код на Python: https://github.com/dankonikolic/Scaled-Correlation