В информатике алгоритм поиска — это алгоритм, разработанный для решения задачи поиска . Алгоритмы поиска работают для извлечения информации, хранящейся в определенной структуре данных или вычисляемой в поисковом пространстве проблемной области, с дискретными или непрерывными значениями .
Хотя поисковые системы используют алгоритмы поиска, они относятся к области изучения поиска информации , а не алгоритмики.
Соответствующий алгоритм поиска часто зависит от структуры данных, в которой выполняется поиск, и может также включать в себя предварительные знания о данных. Алгоритмы поиска могут быть сделаны более быстрыми или эффективными с помощью специально созданных структур баз данных, таких как деревья поиска , хэш-карты и индексы баз данных . [1] [2]
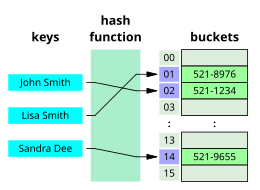
Алгоритмы поиска можно классифицировать на основе их механизма поиска на три типа алгоритмов: линейные, бинарные и хеширующие. Линейные алгоритмы поиска проверяют каждую запись на наличие связанной с целевым ключом линейно. [3] Двоичные, или полуинтервальные, поиски многократно нацелены на центр структуры поиска и делят пространство поиска пополам. Алгоритмы сравнительного поиска улучшают линейный поиск, последовательно исключая записи на основе сравнений ключей, пока не будет найдена целевая запись, и могут применяться к структурам данных в определенном порядке. [4] Цифровые алгоритмы поиска работают на основе свойств цифр в структурах данных с использованием числовых ключей. [5] Наконец, хеширование напрямую сопоставляет ключи с записями на основе хеш-функции . [6]
Алгоритмы часто оцениваются по их вычислительной сложности или максимальному теоретическому времени выполнения. Например, функции двоичного поиска имеют максимальную сложность O (log n ) или логарифмическое время. Проще говоря, максимальное количество операций, необходимых для нахождения цели поиска, является логарифмической функцией размера пространства поиска.
Конкретные приложения алгоритмов поиска включают в себя:
Алгоритмы поиска виртуальных пространств используются в задаче удовлетворения ограничений , где цель состоит в том, чтобы найти набор назначений значений определенным переменным, которые будут удовлетворять определенным математическим уравнениям и неравенствам / равенствам. Они также используются, когда цель состоит в том, чтобы найти назначение переменных, которое максимизирует или минимизирует определенную функцию этих переменных. Алгоритмы для этих задач включают базовый поиск методом грубой силы (также называемый «наивным» или «неинформированным» поиском) и различные эвристики , которые пытаются использовать частичные знания о структуре этого пространства, такие как линейная релаксация, генерация ограничений и распространение ограничений .
Важным подклассом являются методы локального поиска , которые рассматривают элементы пространства поиска как вершины графа с ребрами, определенными набором эвристик, применимых к случаю; и сканируют пространство, перемещаясь от элемента к элементу вдоль ребер, например, в соответствии с критерием наискорейшего спуска или критерием лучшего первого , или в стохастическом поиске . Эта категория включает в себя большое разнообразие общих метаэвристических методов, таких как имитация отжига , поиск с запретами , A-команды и генетическое программирование , которые объединяют произвольные эвристики определенным образом. Противоположностью локальному поиску были бы методы глобального поиска. Этот метод применим, когда пространство поиска не ограничено, и все аспекты данной сети доступны для сущности, запускающей алгоритм поиска. [7]
Этот класс также включает различные алгоритмы поиска по дереву , которые рассматривают элементы как вершины дерева и обходят это дерево в некотором специальном порядке. Примерами последних являются исчерпывающие методы, такие как поиск в глубину и поиск в ширину , а также различные эвристические методы обрезки дерева поиска, такие как возврат и ветвь и граница . В отличие от общих метаэвристик, которые в лучшем случае работают только в вероятностном смысле, многие из этих методов поиска по дереву гарантированно находят точное или оптимальное решение, если им дать достаточно времени. Это называется « полнота ».
Другой важный подкласс состоит из алгоритмов для исследования игрового дерева многопользовательских игр, таких как шахматы или нарды , узлы которых состоят из всех возможных игровых ситуаций, которые могут возникнуть из текущей ситуации. Цель этих задач — найти ход, который обеспечивает наилучшие шансы на победу, принимая во внимание все возможные ходы противника(ов). Похожие проблемы возникают, когда людям или машинам приходится принимать последовательные решения, результаты которых не полностью находятся под контролем, например, при управлении роботом или в маркетинговом , финансовом или военном стратегическом планировании. Этот тип задач — комбинаторный поиск — широко изучался в контексте искусственного интеллекта . Примерами алгоритмов для этого класса являются алгоритм минимакса , альфа-бета-обрезка и алгоритм A* и его варианты.
Название «комбинаторный поиск» обычно используется для алгоритмов, которые ищут определенную подструктуру заданной дискретной структуры , такой как граф, строка , конечная группа и т. д. Термин комбинаторная оптимизация обычно используется, когда целью является нахождение подструктуры с максимальным (или минимальным) значением некоторого параметра. (Поскольку подструктура обычно представлена в компьютере набором целочисленных переменных с ограничениями, эти задачи можно рассматривать как особые случаи удовлетворения ограничений или дискретной оптимизации; но они обычно формулируются и решаются в более абстрактной обстановке, где внутреннее представление явно не упоминается.)
Важным и широко изученным подклассом являются графовые алгоритмы , в частности алгоритмы обхода графа , для поиска определенных подструктур в заданном графе — таких как подграфы , пути , контуры и т. д. Примерами являются алгоритм Дейкстры , алгоритм Крускала , алгоритм ближайшего соседа и алгоритм Прима .
Другим важным подклассом этой категории являются алгоритмы поиска строк , которые ищут шаблоны внутри строк. Два известных примера — алгоритмы Бойера–Мура и Кнута–Морриса–Пратта , а также несколько алгоритмов, основанных на структуре данных суффиксного дерева .
В 1953 году американский статистик Джек Кифер разработал поиск Фибоначчи , который можно использовать для нахождения максимума унимодальной функции и который имеет множество других применений в информатике.
Существуют также методы поиска, разработанные для квантовых компьютеров , такие как алгоритм Гровера , которые теоретически быстрее, чем линейный или грубый поиск даже без помощи структур данных или эвристик. Хотя идеи и приложения, лежащие в основе квантовых компьютеров, все еще являются чисто теоретическими, были проведены исследования с использованием алгоритмов, таких как алгоритм Гровера, которые точно воспроизводят гипотетические физические версии квантовых вычислительных систем. [8]
Категории: