Конечный автомат

Математическая модель вычисления

Классы автоматов

Конечный автомат ( FSM ) или конечный автомат ( FSA , множественное число: автоматы ), конечный автомат или просто конечный автомат — это математическая модель вычислений . Это абстрактная машина , которая может находиться ровно в одном из конечного числа состояний в любой момент времени. FSM может переходить из одного состояния в другое в ответ на некоторые входные данные ; изменение из одного состояния в другое называется переходом . ^[1] FSM определяется списком своих состояний, своим начальным состоянием и входными данными, которые запускают каждый переход. Конечные автоматы бывают двух типов — детерминированные конечные автоматы и недетерминированные конечные автоматы . ^[2] Для любого недетерминированного конечного автомата можно построить эквивалентный детерминированный.

Поведение конечных автоматов можно наблюдать во многих устройствах в современном обществе, которые выполняют предопределенную последовательность действий в зависимости от последовательности событий, с которыми они сталкиваются. Простыми примерами являются: торговые автоматы , которые выдают продукты, когда вносится правильная комбинация монет; лифты , последовательность остановок которых определяется этажами, запрашиваемыми пассажирами; светофоры , которые меняют последовательность, когда автомобили ждут; кодовые замки , которые требуют ввода последовательности цифр в правильном порядке.

Конечный автомат имеет меньшую вычислительную мощность, чем некоторые другие модели вычислений, такие как машина Тьюринга . ^[3] Различие в вычислительной мощности означает, что существуют вычислительные задачи, которые может выполнять машина Тьюринга, но не может выполнять конечный автомат. Это происходит потому, что память конечного автомата ограничена числом имеющихся у него состояний. Конечный автомат имеет ту же вычислительную мощность, что и машина Тьюринга, которая ограничена тем, что ее головка может выполнять только операции «чтения» и всегда должна двигаться слева направо. Конечные автоматы изучаются в более общей области теории автоматов .

Пример: турникет с монетоприемником

Диаграмма состояний турникета

Турникет

Примером простого механизма, который может быть смоделирован конечным автоматом, является турникет . [ ^{4] [5]} Турникет, используемый для контроля доступа в метро и парки развлечений, представляет собой ворота с тремя вращающимися рычагами на уровне талии, один из которых находится поперек входа. Изначально рычаги заблокированы, блокируя вход и не позволяя посетителям проходить через них. Вкладывание монеты или жетона в щель на турникете разблокирует рычаги, позволяя одному клиенту пройти. После того, как клиент проходит, рычаги снова блокируются, пока не будет вставлена ​​еще одна монета.

Рассматриваемый как конечный автомат, турникет имеет два возможных состояния: Заблокирован и Разблокирован . ^[4] Существует два возможных входа, которые влияют на его состояние: помещение монеты в щель ( coin ) и нажатие рычага ( push ). В заблокированном состоянии нажатие на рычаг не имеет никакого эффекта; независимо от того, сколько раз дается входной push , он остается в заблокированном состоянии. Помещение монеты — то есть предоставление автомату ввода монеты — изменяет состояние с Locked на Unlocked . В разблокированном состоянии помещение дополнительных монет не имеет никакого эффекта; то есть предоставление дополнительных вводов монет не изменяет состояние. Клиент, проталкивающийся через рычаги, дает вход push и сбрасывает состояние на Locked .

Машину состояний турникета можно представить в виде таблицы переходов состояний , показывающей для каждого возможного состояния переходы между ними (на основе входных данных, поданных в машину) и выходные данные, получаемые в результате каждого входного сигнала:

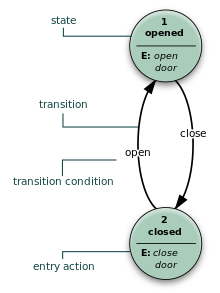
Машина состояний турникета также может быть представлена ​​направленным графом, называемым диаграммой состояний (выше) . Каждое состояние представлено узлом ( кругом ) . Ребра ( стрелки ) показывают переходы из одного состояния в другое. Каждая стрелка помечена входом, который запускает этот переход. Вход, который не вызывает изменения состояния (например, ввод монеты в состоянии Unlocked ), представлен круглой стрелкой, возвращающей в исходное состояние. Стрелка в узел Locked от черной точки указывает, что это начальное состояние.

Понятия и терминология

Состояние — это описание статуса системы, ожидающей выполнения перехода . Переход — это набор действий, которые должны быть выполнены при выполнении условия или при получении события. Например, при использовании аудиосистемы для прослушивания радио (система находится в состоянии «радио») получение стимула «следующий» приводит к переходу на следующую станцию. Когда система находится в состоянии «CD», стимул «следующий» приводит к переходу на следующий трек. Одинаковые стимулы запускают различные действия в зависимости от текущего состояния.

В некоторых представлениях конечных автоматов также возможно связывать действия с состоянием:

• действие входа: выполняется при входе в государство, и
• действие выхода: выполняется при выходе из состояния.

Представления

Рис. 1 Пример диаграммы состояний UML (тостер)

Рис. 2 Пример конечного автомата SDL

Рис. 3 Пример простого конечного автомата

Таблица состояний/событий

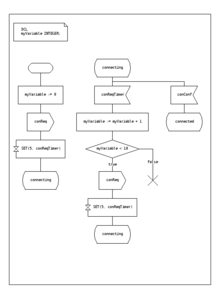
Используется несколько типов таблиц переходов состояний . Наиболее распространенное представление показано ниже: комбинация текущего состояния (например, B) и ввода (например, Y) показывает следующее состояние (например, C). Полная информация о действии не описана напрямую в таблице и может быть добавлена ​​только с помощью сносок. ^{[ необходимо дополнительное объяснение ]} Определение FSM, включающее полную информацию о действии, возможно с использованием таблиц состояний (см. также виртуальный конечный автомат ).

Конечные автоматы UML

Унифицированный язык моделирования имеет нотацию для описания конечных автоматов. Конечные автоматы UML преодолевают ограничения ^{[ требуется ссылка ]} традиционных конечных автоматов, сохраняя при этом свои основные преимущества. Конечные автоматы UML вводят новые концепции иерархически вложенных состояний и ортогональных областей , расширяя при этом понятие действий . Конечные автоматы UML обладают характеристиками как автоматов Мили , так и автоматов Мура . Они поддерживают действия, зависящие как от состояния системы, так и от события -триггера , как в автоматах Мили, а также действия входа и выхода , которые связаны с состояниями, а не с переходами, как в автоматах Мура. ^{[ требуется ссылка ]}

Конечные автоматы SDL

Язык спецификаций и описаний — это стандарт МСЭ , включающий графические символы для описания действий при переходе:

• отправить событие
• получить событие
• запустить таймер
• отменить таймер
• запустить еще одну машину с параллельными состояниями
• решение

SDL встраивает базовые типы данных, называемые «абстрактными типами данных», язык действий и семантику выполнения, чтобы сделать конечный автомат исполняемым. ^{[ необходима ссылка ]}

Другие диаграммы состояний

Существует большое количество вариантов представления конечного автомата, подобного показанному на рисунке 3.

Использование

Помимо использования в моделировании реактивных систем, представленных здесь, конечные автоматы играют важную роль во многих различных областях, включая электротехнику , лингвистику , информатику , философию , биологию , математику , программирование видеоигр и логику . Конечные автоматы — это класс автоматов, изучаемых в теории автоматов и теории вычислений . В информатике конечные автоматы широко используются в моделировании поведения приложений ( теория управления ), проектировании аппаратных цифровых систем , программной инженерии , компиляторах , сетевых протоколах и вычислительной лингвистике .

Классификация

Конечные автоматы можно разделить на акцепторы, классификаторы, преобразователи и секвенсоры. ^[6]

Акцепторы

Рис. 4: Конечный автомат-акцептор: анализ строки «nice».

Рис. 5: Представление акцептора; в этом примере показано, как определить, содержит ли двоичное число четное количество нулей, где S ₁ — принимающее состояние , а S ₂ — не принимающее состояние .

Акцепторы (также называемые детекторами или распознавателями ) выдают двоичный вывод, указывающий, принят ли полученный ввод. Каждое состояние акцептора либо принимает, либо не принимает . После того, как весь ввод был получен, если текущее состояние является принимающим, ввод принимается; в противном случае он отклоняется. Как правило, ввод представляет собой последовательность символов (знаков); действия не используются. Начальное состояние также может быть принимающим, и в этом случае акцептор принимает пустую строку. Пример на рисунке 4 показывает акцептор, который принимает строку «nice». В этом акцепторе единственным принимающим состоянием является состояние 7.

(Возможно, бесконечное) множество последовательностей символов, называемое формальным языком , является регулярным языком , если существует некоторый акцептор, который принимает именно этот набор. Например, множество двоичных строк с четным числом нулей является регулярным языком (ср. рис. 5), тогда как множество всех строк, длина которых является простым числом, не является таковым. ^{[7] : 18, 71}

Акцептор также может быть описан как определяющий язык, который будет содержать каждую строку, принятую акцептором, но ни одну из отклоненных; этот язык принимается акцептором . По определению, языки, принимаемые акцепторами, являются регулярными языками .

Задача определения языка, принимаемого данным акцептором, является примером задачи алгебраического пути , которая сама по себе является обобщением задачи кратчайшего пути на графы с ребрами, взвешенными элементами (произвольного) полукольца . ^{[8] [9] [ жаргон ]}

Пример принимающего состояния показан на рис. 5: детерминированный конечный автомат (ДКА), который определяет, содержит ли двоичная входная строка четное число нулей.

S ₁ (которое также является начальным состоянием) указывает состояние, в котором было введено четное число нулей. Таким образом, S ₁ является принимающим состоянием. Этот акцептор завершит работу в принимающем состоянии, если двоичная строка содержит четное число нулей (включая любую двоичную строку, не содержащую нулей). Примерами строк, принимаемых этим акцептором, являются ε ( пустая строка ), 1, 11, 11..., 00, 010, 1010, 10110 и т. д.

Классификаторы

Классификаторы являются обобщением акцепторов, которые производят n- арный вывод, где n строго больше двух. ^[10]

Преобразователи

Рис. 6 Преобразователь FSM: пример модели Мура

Рис. 7 Преобразователь FSM: пример модели Мили

Преобразователи производят вывод на основе заданного ввода и/или состояния с использованием действий. Они используются для приложений управления и в области вычислительной лингвистики .

В приложениях управления различают два типа:

машина Мура

FSM использует только действия входа, т. е. выход зависит только от состояния. Преимущество модели Мура заключается в упрощении поведения. Рассмотрим дверь лифта. Конечный автомат распознает две команды: «command_open» и «command_close», которые вызывают изменение состояния. Действие входа (E:) в состоянии «Opening» запускает двигатель, открывающий дверь, действие входа в состоянии «Closing» запускает двигатель в другом направлении, закрывая дверь. Состояния «Opened» и «Closed» останавливают двигатель при полном открытии или закрытии. Они сигнализируют внешнему миру (например, другим конечным автоматам) о ситуации: «дверь открыта» или «дверь закрыта».

Машина для помола муки

FSM также использует входные действия, т. е. выход зависит от входа и состояния. Использование автомата Мили часто приводит к сокращению числа состояний. Пример на рисунке 7 показывает автомат Мили, реализующий то же поведение, что и в примере Мура (поведение зависит от реализованной модели выполнения FSM и будет работать, например, для виртуального FSM , но не для управляемого событиями FSM ). Существует два входных действия (I:): «запустить двигатель, чтобы закрыть дверь, если поступает команда command_close» и «запустить двигатель в другом направлении, чтобы открыть дверь, если поступает команда command_open». Промежуточные состояния «открытие» и «закрытие» не показаны.

Секвенсоры

Секвенсоры (также называемые генераторами ) являются подклассом акцепторов и преобразователей, которые имеют однобуквенный входной алфавит. Они производят только одну последовательность, которую можно рассматривать как выходную последовательность выходов акцептора или преобразователя. ^[6]

Детерминизм

Еще одно различие — между детерминированными ( DFA ) и недетерминированными ( NFA , GNFA ) автоматами. В детерминированном автомате каждое состояние имеет ровно один переход для каждого возможного входа. В недетерминированном автомате вход может привести к одному, более чем одному или отсутствию перехода для данного состояния. Алгоритм построения powerset может преобразовать любой недетерминированный автомат в (обычно более сложный) детерминированный автомат с идентичной функциональностью.

Конечный автомат с единственным состоянием называется «комбинаторным FSM». Он допускает действия только при переходе в состояние. Эта концепция полезна в случаях, когда требуется совместная работа нескольких конечных автоматов, и когда удобно рассматривать чисто комбинаторную часть как форму FSM для соответствия инструментам проектирования. ^[11]

Альтернативная семантика

Существуют и другие наборы семантик, которые можно использовать для представления конечных автоматов. Например, существуют инструменты для моделирования и проектирования логики для встроенных контроллеров. ^[12] Они объединяют иерархические конечные автоматы (обычно имеющие более одного текущего состояния), потоковые графы и таблицы истинности в один язык, что приводит к другому формализму и набору семантик. ^[13] Эти диаграммы, как и оригинальные конечные автоматы Харела , ^[14] поддерживают иерархически вложенные состояния, ортогональные области , действия состояний и действия переходов. ^[15]

Математическая модель

В соответствии с общей классификацией встречаются следующие формальные определения.

Детерминированный конечный автомат или детерминированный конечный акцептор представляет собой пятерку , где: ${\displaystyle (\Sigma ,S,s_{0},\delta ,F)}$

• ${\displaystyle \Sigma }$— входной алфавит (конечный непустой набор символов);
• ${\displaystyle S}$— конечное непустое множество состояний;
• ${\displaystyle s_{0}}$— начальное состояние, элемент ; ${\displaystyle S}$
• ${\displaystyle \delta }$— функция перехода состояний: (в недетерминированном конечном автомате она была бы , т.е. возвращала бы набор состояний); ${\displaystyle \delta :S\times \Sigma \rightarrow S}$ ${\displaystyle \delta :S\times \Sigma \rightarrow {\mathcal {P}}(S)}$ ${\displaystyle \delta }$
• ${\displaystyle F}$— это множество конечных состояний, (возможно пустое) подмножество . ${\displaystyle S}$

Как для детерминированных, так и для недетерминированных FSM принято разрешать быть частичной функцией , т. е. не обязательно определять для каждой комбинации и . Если FSM находится в состоянии , следующим символом является и не определен, то может объявить об ошибке (т. е. отклонить ввод). Это полезно в определениях машин общего состояния, но менее полезно при преобразовании машины. Некоторые алгоритмы в их форме по умолчанию могут требовать полных функций. ${\displaystyle \delta }$ ${\displaystyle \delta (s,x)}$ ${\displaystyle s\in S}$ ${\displaystyle x\in \Sigma }$ ${\displaystyle M}$ ${\displaystyle s}$ ${\displaystyle x}$ ${\displaystyle \delta (s,x)}$ ${\displaystyle M}$

Конечный автомат имеет ту же вычислительную мощность, что и машина Тьюринга , которая ограничена таким образом, что ее головка может выполнять только операции «чтения» и всегда должна двигаться слева направо. То есть, каждый формальный язык, принятый конечным автоматом, принимается таким видом ограниченной машины Тьюринга, и наоборот. ^[16]

Конечный преобразователь представляет собой шестерку , где: ${\displaystyle (\Sigma ,\Gamma ,S,s_{0},\delta ,\omega )}$

• ${\displaystyle \Sigma }$— входной алфавит (конечный непустой набор символов);
• ${\displaystyle \Gamma }$— выходной алфавит (конечный непустой набор символов);
• ${\displaystyle S}$— конечное непустое множество состояний;
• ${\displaystyle s_{0}}$— начальное состояние, элемент ; ${\displaystyle S}$
• ${\displaystyle \delta }$— функция перехода состояний: ; ${\displaystyle \delta :S\times \Sigma \rightarrow S}$
• ${\displaystyle \omega }$— выходная функция.

Если выходная функция зависит от состояния и входного символа ( ), то определение соответствует модели Мили и может быть смоделировано как автомат Мили . Если выходная функция зависит только от состояния ( ), то определение соответствует модели Мура и может быть смоделировано как автомат Мура . Конечный автомат без выходной функции вообще называется полуавтоматом или системой переходов . ${\displaystyle \omega :S\times \Sigma \rightarrow \Gamma }$ ${\displaystyle \omega :S\rightarrow \Gamma }$

Если мы проигнорируем первый выходной символ автомата Мура, , то его можно легко преобразовать в эквивалентный по выходу автомат Мили, установив выходную функцию каждого перехода Мили (т. е. маркируя каждое ребро) выходным символом, заданным для конечного состояния Мура. Обратное преобразование менее просто, поскольку состояние автомата Мили может иметь разные выходные метки на своих входящих переходах (ребрах). Каждое такое состояние должно быть разделено на несколько состояний автомата Мура, по одному для каждого инцидентного выходного символа. ^[17] ${\displaystyle \omega (s_{0})}$

Оптимизация

Оптимизация FSM означает поиск машины с минимальным числом состояний, которая выполняет ту же функцию. Самый быстрый известный алгоритм, делающий это, — алгоритм минимизации Хопкрофта . ^{[18] [19]} Другие методы включают использование таблицы импликации или процедуры редукции Мура. ^[20] Кроме того, ациклические FSA могут быть минимизированы за линейное время . ^[21]

Выполнение

Аппаратные приложения

Рис. 9. Принципиальная схема 4-битного ТТЛ- счетчика, разновидность конечного автомата.

В цифровой схеме FSM может быть построен с использованием программируемого логического устройства , программируемого логического контроллера , логических вентилей и триггеров или реле . Более конкретно, для аппаратной реализации требуется регистр для хранения переменных состояния, блок комбинационной логики , который определяет переход состояния, и второй блок комбинационной логики, который определяет выход FSM. Одной из классических аппаратных реализаций является контроллер Ричардса .

В машине Медведева выход напрямую подключен к триггерам состояния, что минимизирует временную задержку между триггерами и выходом. ^{[22] [23]}

Благодаря кодированию состояний для машин с низким энергопотреблением можно оптимизировать потребление энергии.

Программные приложения

Для создания программных приложений с использованием конечных автоматов обычно используются следующие концепции:

• Автоматизированное программирование
• Конечный автомат, управляемый событиями
• Виртуальный конечный автомат
• Государственный шаблон дизайна

Конечные автоматы и компиляторы

Конечные автоматы часто используются в интерфейсе компиляторов языков программирования. Такой интерфейс может включать несколько конечных автоматов, которые реализуют лексический анализатор и парсер. Начиная с последовательности символов, лексический анализатор строит последовательность языковых токенов (таких как зарезервированные слова, литералы и идентификаторы), из которых парсер строит синтаксическое дерево. Лексический анализатор и парсер обрабатывают обычные и контекстно-свободные части грамматики языка программирования. ^[24]

Смотрите также

• Абстрактные конечные автоматы
• Конечный автомат с переменным конечным числом
• Коммуникационный конечный автомат
• Система управления
• Контрольный стол
• Таблицы решений
• РАЗРАБОТЧИКИ
• Скрытая марковская модель
• сеть Петри
• Автомат Pushdown
• Квантовый конечный автомат
• SCXML
• Полуавтомат
• Действие полугруппы
• Последовательная логика
• Диаграмма состояний
• Синхронизирующее слово
• Полугруппа преобразований
• Система перехода
• Дерево автомата
• машина Тьюринга
• Конечный автомат UML

Ссылки

1. Ван, Цзяцунь (2019). Формальные методы в информатике . CRC Press. стр. 34. ISBN 978-1-4987-7532-8.
2. "Конечные автоматы – Brilliant Math & Science Wiki". brilliant.org . Получено 14.04.2018 .
3. Белзер, Джек; Хольцман, Альберт Джордж; Кент, Аллен (1975). Энциклопедия компьютерных наук и технологий. Т. 25. США: CRC Press. стр. 73. ISBN 978-0-8247-2275-3.
4. Koshy, Thomas (2004). Дискретная математика с приложениями. Academic Press. стр. 762. ISBN 978-0-12-421180-3.
5. Райт, Дэвид Р. (2005). "Конечные автоматы" (PDF) . Заметки о классе CSC215 . Веб-сайт Дэвида Р. Райта, N. Carolina State Univ. Архивировано из оригинала (PDF) 27.03.2014 . Получено 14.07.2012 .
6. Келлер, Роберт М. (2001). "Классификаторы, акцепторы, преобразователи и секвенаторы" (PDF) . Компьютерные науки: от абстракции к реализации (PDF) . Колледж Харви Мадда. стр. 480.
7. Джон Э. Хопкрофт и Джеффри Д. Ульман (1979). Введение в теорию автоматов, языки и вычисления. Reading/MA: Addison-Wesley. ISBN 978-0-201-02988-8.
8. Pouly, Marc; Kohlas, Jürg (2011). Generic Inference: A Unifying Theory for Automated Reasoning . John Wiley & Sons. Глава 6. Valuation Algebras for Path Problems, стр. 223 в частности. ISBN 978-1-118-01086-0.
9. Яцек Йонци (июнь 2008 г.). "Алгебраические задачи пути" (PDF) . Архивировано из оригинала (PDF) 2014-08-21 . Получено 2014-08-20 ., стр. 34
10. Фелкин, М. (2007). Гийе, Фабрис; Гамильтон, Ховард Дж. (ред.). Меры качества в интеллектуальном анализе данных - Исследования в области вычислительного интеллекта . Т. 43. Springer, Берлин, Гейдельберг. С. 277–278. doi :10.1007/978-3-540-44918-8_12. ISBN 978-3-540-44911-9.
11. Brutscheck, M., Berger, S., Franke, M., Schwarzbacher, A., Becker, S.: Structural Division Procedure for Efficient IC Analysis. IET Irish Signals and Systems Conference (ISSC 2008), стр. 18–23. Голуэй, Ирландия, 18–19 июня 2008 г. [1]
12. "Тивари, А. (2002). Формальная семантика и методы анализа для моделей Simulink Stateflow" (PDF) . sri.com . Получено 14.04.2018 .
13. Хамон, Г. (2005). Денотационная семантика для Stateflow . Международная конференция по встроенному программному обеспечению. Джерси-Сити, Нью-Джерси: ACM. С. 164–172. CiteSeerX 10.1.1.89.8817 . 
14. "Harel, D. (1987). Визуальный формализм для сложных систем. Наука компьютерного программирования, 231–274" (PDF) . Архивировано из оригинала (PDF) 2011-07-15 . Получено 2011-06-07 .
15. "Alur, R., Kanade, A., Ramesh, S., & Shashidhar, KC (2008). Символический анализ для улучшения покрытия моделирования моделей Simulink/Stateflow. Международная конференция по встроенному программному обеспечению (стр. 89–98). Атланта, Джорджия: ACM" (PDF) . Архивировано из оригинала (PDF) 2011-07-15.
16. Black, Paul E (12 мая 2008 г.). «Конечный автомат». Словарь алгоритмов и структур данных . Национальный институт стандартов и технологий США . Архивировано из оригинала 13 октября 2018 г. Получено 2 ноября 2016 г.
17. Андерсон, Джеймс Эндрю; Хэд, Томас Дж. (2006). Теория автоматов с современными приложениями. Cambridge University Press. С. 105–108. ISBN 978-0-521-84887-9.
18. Хопкрофт, Джон Э. (1971). Алгоритм n log n для минимизации состояний в конечном автомате (PDF) (Технический отчет). Т. CS-TR-71-190. Стэнфордский университет.^{[ постоянная мертвая ссылка ]}
19. Алмейда, Марко; Морейра, Нельма; Рейс, Роджерио (2007). О работе алгоритмов минимизации автоматов (PDF) (Технический отчет). Том. ДКК-2007-03. Университет Порто. Архивировано из оригинала (PDF) 17 января 2009 года . Проверено 25 июня 2008 г.
20. Эдвард Ф. Мур (1956). CE Шеннон и Дж. Маккарти (ред.). «Gedanken-Experiments on Sequential Machines». Annals of Mathematics Studies . 34. Princeton University Press: 129–153.Здесь: Теорема 4, стр.142.
21. Ревуз, Д. (1992). «Минимизация ациклических автоматов за линейное время». Теоретическая информатика . 92 : 181–189. doi : 10.1016/0304-3975(92)90142-3.
22. Kaeslin, Hubert (2008). "Мили, Мур, Медведев-тип и комбинаторные выходные биты". Digital Integrated Circuit Design: From VLSI Architectures to CMOS Fabrication . Cambridge University Press. стр. 787. ISBN 978-0-521-88267-5.
23. Слайды, архивированные 18 января 2017 г. в Wayback Machine , Синхронные конечные автоматы; Проектирование и поведение , Университет прикладных наук Гамбурга , стр. 18
24. Ахо, Альфред В.; Сети , Рави ; Ульман, Джеффри Д. (1986). Составители: принципы, методы и инструменты (1-е изд.). Addison-Wesley . ISBN 978-0-201-10088-4.

Дальнейшее чтение

Общий

• Сакарович, Жак (2009). Элементы теории автоматов . Перевод с французского Рубена Томаса. Cambridge University Press . ISBN 978-0-521-84425-3. Збл  1188.68177.
• Вагнер, Ф., «Моделирование программного обеспечения с помощью конечных автоматов: практический подход», Auerbach Publications, 2006, ISBN 0-8493-8086-3 . 
• ITU-T, Рекомендация Z.100 Язык спецификации и описания (SDL)
• Самек, М., Практические диаграммы состояний в C/C++, CMP Books, 2002, ISBN 1-57820-110-1 . 
• Самек, М., Практические диаграммы состояний UML в C/C++, 2-е издание, Newnes, 2008, ISBN 0-7506-8706-1 . 
• Гарднер, Т., Расширенное государственное управление. Архивировано 19 ноября 2008 г. в Wayback Machine , 2007 г.
• Кассандр, К., Лафортюн, С., «Введение в дискретные событийные системы». Kluwer, 1999, ISBN 0-7923-8609-4 . 
• Тимоти Кам, Синтез конечных автоматов: функциональная оптимизация . Kluwer Academic Publishers, Бостон, 1997, ISBN 0-7923-9842-4 
• Тициано Вилла, Синтез конечных автоматов: логическая оптимизация . Kluwer Academic Publishers, Бостон, 1997, ISBN 0-7923-9892-0 
• Кэрролл, Дж., Лонг, Д., Теория конечных автоматов с введением в формальные языки . Prentice Hall, Englewood Cliffs, 1989.
• Кохави, З., Теория коммутации и конечных автоматов . McGraw-Hill, 1978.
• Гилл, А., Введение в теорию конечных автоматов . McGraw-Hill, 1962.
• Гинзбург, С., Введение в теорию математических машин . Addison-Wesley, 1962.

Конечные автоматы (теория автоматов) в теоретической информатике

• Арбиб, Майкл А. (1969). Теории абстрактных автоматов (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice-Hall, Inc. ISBN 978-0-13-913368-8.
• Бобров, Леонард С.; Арбиб, Майкл А. (1974). Дискретная математика: прикладная алгебра для вычислительной техники и информационной науки (1-е изд.). Филадельфия: WB Saunders Company, Inc. ISBN 978-0-7216-1768-8.
• Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc. Номер в каталоге карточек Библиотеки Конгресса 67-25924.
• Булос, Джордж; Джеффри, Ричард (1999) [1989]. Вычислимость и логика (3-е изд.). Кембридж, Англия: Cambridge University Press. ISBN 978-0-521-20402-6.
• Брукшир, Дж. Гленн (1989). Теория вычислений: формальные языки, автоматы и сложность . Редвуд-Сити, Калифорния: Benjamin/Cummings Publish Company, Inc. ISBN 978-0-8053-0143-4.
• Дэвис, Мартин; Сигал, Рон; Вейукер, Элейн Дж. (1994). Вычислимость, сложность, языки и логика: основы теоретической информатики (2-е изд.). Сан-Диего: Academic Press, Harcourt, Brace & Company. ISBN 978-0-12-206382-4.
• Хопкрофт, Джон; Ульман, Джеффри (1979). Введение в теорию автоматов, языки и вычисления (1-е изд.). Массовое чтение: Addison-Wesley. ISBN 978-0-201-02988-8.
• Хопкрофт, Джон Э.; Мотвани, Раджив; Ульман, Джеффри Д. (2001). Введение в теорию автоматов, языки и вычисления (2-е изд.). Массовое чтение: Addison-Wesley. ISBN 978-0-201-44124-6.
• Хопкин, Дэвид; Мосс, Барбара (1976). Автоматы . Нью-Йорк: Эльзевир Северная Голландия. ISBN 978-0-444-00249-5.
• Козен, Декстер К. (1997). Автоматы и вычислимость (1-е изд.). Нью-Йорк: Springer-Verlag. ISBN 978-0-387-94907-9.
• Льюис, Гарри Р.; Пападимитриу , Христос Х. (1998). Элементы теории вычислений (2-е изд.). Верхняя Сэддл-Ривер, Нью-Джерси: Prentice-Hall. ISBN 978-0-13-262478-7.
• Линц, Питер (2006). Формальные языки и автоматы (4-е изд.). Садбери, Массачусетс: Джонс и Бартлетт. ISBN 978-0-7637-3798-6.
• Минский, Марвин (1967). Вычисления: Конечные и бесконечные машины (1-е изд.). Нью-Джерси: Prentice-Hall.
• Пападимитриу, Христос (1993). Computational Complexity (1-е изд.). Эддисон Уэсли. ISBN 978-0-201-53082-7.
• Пиппенджер, Николас (1997). Теории вычислимости (1-е изд.). Кембридж, Англия: Cambridge University Press. ISBN 978-0-521-55380-3.
• Роджер, Сьюзен; Финли, Томас (2006). JFLAP: интерактивные формальные языки и пакет автоматов (1-е изд.). Садбери, Массачусетс: Jones and Bartlett. ISBN 978-0-7637-3834-1.
• Sipser, Michael (2006). Введение в теорию вычислений (2-е изд.). Boston Mass: Thomson Course Technology. ISBN 978-0-534-95097-2.
• Вуд, Дерик (1987). Теория вычислений (1-е изд.). Нью-Йорк: Harper & Row, Publishers, Inc. ISBN 978-0-06-047208-5.

Абстрактные машины состояний в теоретической информатике

• Гуревич, Юрий (июль 2000 г.). "Последовательные абстрактные конечные автоматы захватывают последовательные алгоритмы" (PDF) . ACM Transactions on Computational Logic . 1 (1): 77–111. CiteSeerX  10.1.1.146.3017 . doi :10.1145/343369.343384. S2CID  2031696.

Машинное обучение с использованием конечных алгоритмов

• Митчелл, Том М. (1997). Машинное обучение (1-е изд.). Нью-Йорк: WCB/McGraw-Hill Corporation. ISBN 978-0-07-042807-2.

Аппаратная инженерия: минимизация состояний и синтез последовательных цепей

• Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc. Номер в каталоге карточек Библиотеки Конгресса 67-25924.
• Бут, Тейлор Л. (1971). Цифровые сети и компьютерные системы (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc. ISBN 978-0-471-08840-0.
• МакКласки, Э. Дж. (1965). Введение в теорию коммутационных цепей (1-е изд.). Нью-Йорк: McGraw-Hill Book Company, Inc. Номер каталога карточек Библиотеки Конгресса 65-17394.
• Хилл, Фредрик Дж.; Петерсон, Джеральд Р. (1965). Введение в теорию коммутационных цепей (1-е изд.). Нью-Йорк: McGraw-Hill Book Company. Номер каталога карточек Библиотеки Конгресса 65-17394.

Конечные цепные процессы Маркова

«Мы можем рассматривать цепь Маркова как процесс, который последовательно проходит через набор состояний s ₁ , s ₂ , …, s _r . … если он находится в состоянии s _{i ,} он переходит к следующей остановке в состояние s _j с вероятностью p _ij . Эти вероятности можно представить в виде матрицы перехода» (Кемени (1959), стр. 384)

Конечные процессы цепи Маркова также известны как подсдвиги конечного типа .

• Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc. Номер в каталоге карточек Библиотеки Конгресса 67-25924.
• Кемени, Джон Г.; Миркил, Хазлтон; Снелл, Дж. Лори; Томпсон, Джеральд Л. (1959). Конечные математические структуры (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice-Hall, Inc. Номер в каталоге карточек Библиотеки Конгресса 59-12841.Глава 6 «Конечные цепи Маркова».

Внешние ссылки

• Моделирование поведения простого ИИ с использованием конечного автомата. Пример использования в видеоиграх
• Бесплатный онлайн-словарь по вычислительной технике с описанием конечных автоматов
• Словарь алгоритмов и структур данных NIST, описание конечных автоматов
• Краткий обзор типов конечных автоматов, сравнение теоретических аспектов конечных автоматов Мили, Мура, Харела и UML.