Теорема Стейница

Теоретико-графовое описание многогранников

В полиэдральной комбинаторике , разделе математики, теорема Стейница представляет собой характеристику неориентированных графов, образованных ребрами и вершинами трехмерных выпуклых многогранников : они в точности представляют собой 3-связные плоские графы . То есть каждый выпуклый многогранник образует 3-связный плоский граф, и каждый 3-связный плоский граф можно представить как график выпуклого многогранника. По этой причине 3-связные плоские графы также известны как многогранные графы . ^[1]

Этот результат дает классификационную теорему для трехмерных выпуклых многогранников, чего не известно в более высоких измерениях. ^[2] Он обеспечивает полное и чисто комбинаторное описание графиков этих многогранников, позволяя легче доказывать другие результаты о них, такие как теорема Эберхарда о реализации многогранников с заданными типами граней, без обращения к геометрии. этих фигур. ^[3] Кроме того, он применялся при рисовании графиков как способ создания трехмерной визуализации абстрактных графов. ^[4] Бранко Грюнбаум назвал эту теорему «самым важным и глубоким известным результатом о 3-многогранниках ». ^[5]

Теорема появляется в публикации Эрнста Стейница 1922 года ^[6] , в честь которого она названа. Это можно доказать с помощью математической индукции (как это сделал Стейниц), найдя состояние с минимальной энергией двумерной пружинной системы и перенося результат в три измерения, или используя теорему об упаковке кругов . Известно несколько расширений теоремы, в которых многогранник, реализующий заданный граф, имеет дополнительные ограничения; например, каждый граф многогранника является графиком выпуклого многогранника с целочисленными координатами или графиком выпуклого многогранника, все ребра которого касаются общей средней сферы .

Определения и формулировка теоремы

Освещение скелета выпуклого многогранника источником света, близким к одной из его граней, приводит к тому, что его тени образуют плоскую диаграмму Шлегеля .

Неориентированный граф — это система вершин и ребер , каждое ребро соединяет две вершины. Как это принято в теории графов, для целей теоремы Стейница эти графы ограничены конечными (вершины и ребра представляют собой конечные множества ) и простыми (никакие два ребра не соединяют одни и те же две вершины, и ни одно ребро не соединяет вершину с самой собой). . Из любого многогранника можно составить граф, поставив вершины графа в соответствие вершинам многогранника и соединив любые две вершины графа ребром, если соответствующие две вершины многогранника являются концами ребра многогранника. Этот граф известен как скелет многогранника. ^[7]

Граф является плоским, если его вершины можно изобразить в виде точек на евклидовой плоскости , а его ребра — в виде кривых, соединяющих эти точки, так, чтобы никакие две реберные кривые не пересекались друг с другом и чтобы точка, представляющая вершину, лежала на кривой. представляющий ребро только тогда, когда вершина является конечной точкой ребра. По теореме Фари каждый плоский рисунок можно выпрямить так, что кривые, представляющие края, станут отрезками прямых . Граф называется 3-связным, если он имеет более трех вершин и после удаления любых двух его вершин любая другая пара вершин остается связанной путем. Теорема Стейница утверждает, что эти два условия одновременно необходимы и достаточны для характеристики скелетов трехмерных выпуклых многогранников: данный граф является графиком выпуклого трехмерного многогранника тогда и только тогда, когда он плоский и 3-вершинно связный. ^{[5] [8]} ${\displaystyle G}$ ${\displaystyle G}$

Доказательства

Иллюстрация доказательства теоремы Балинского , показывающая нулевое множество линейной функции (синий), проходящей через две заданные вершины (желтый), и пути симплексного метода, соединяющие оставшийся граф (зеленый).

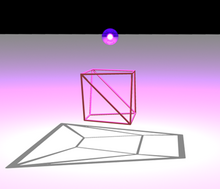
Одно направление теоремы Стейница (направление, которое легче доказать) гласит, что график каждого выпуклого многогранника плоский и 3-связный. Как показано на иллюстрации, планарность можно показать с помощью диаграммы Шлегеля : если разместить источник света возле одной грани многогранника, а плоскость — с другой стороны, тени ребер многогранника образуют плоский граф, вложенный таким образом, чтобы края представляли собой отрезки прямых линий. 3-связность многогранного графа является частным случаем теоремы Балинского о том, что график любого -мерного выпуклого многогранника -связен . Связность графа многогранника после удаления любой его вершины можно доказать, выбрав еще одну вершину , найдя линейную функцию , равную нулю на результирующем множестве вершин, и следуя по путям, сгенерированным симплекс-методом для соединения каждая вершина связана с одной из двух крайних вершин линейной функции, причем выбранная вершина соединена с обеими. ^[9] ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k-1}$ ${\displaystyle v}$ ${\displaystyle k}$ ${\displaystyle v}$

Другое, более сложное направление теоремы Стейница утверждает, что каждый плоский 3-связный граф является графиком выпуклого многогранника. Для этой части есть три стандартных подхода: доказательства по индукции, подъем двумерных вложений Тутте в три измерения с использованием соответствия Максвелла – Кремоны и методы, использующие теорему об упаковке кругов для создания канонического многогранника .

Индукция

ΔY- и YΔ-преобразования многогранника

Хотя исходное доказательство Стейница не было выражено в терминах теории графов, оно может быть переписано в этих терминах и включает в себя поиск последовательности ΔY- и YΔ-преобразований , которые сводят любой 3-связный плоский граф к , графику тетраэдра. YΔ-преобразование удаляет вершину третьей степени из графа, добавляя ребра между всеми ее бывшими соседями, если эти ребра еще не существовали; обратное преобразование, ΔY-преобразование, удаляет ребра треугольника из графа и заменяет их новой вершиной третьей степени, смежной с теми же тремя вершинами. Как только такая последовательность найдена, ее можно перевернуть и преобразовать в геометрические операции, которые шаг за шагом создают желаемый многогранник, начиная с тетраэдра. Каждое YΔ-преобразование в обратной последовательности можно выполнить геометрически, отсекая вершину третьей степени от многогранника. ΔY-преобразование в обратной последовательности может быть выполнено геометрически путем удаления треугольной грани из многогранника и продления соседних граней до точки их пересечения, но только тогда, когда эта тройная точка пересечения трех соседних граней находится на дальней стороне многогранника. удаленную грань многогранника. Когда точка тройного пересечения не находится на дальней стороне этой грани, достаточно проективного преобразования многогранника, чтобы переместить его на правильную сторону. Следовательно, путем индукции по количеству ΔY- и YΔ-преобразований, необходимых для сведения данного графа к , каждый многогранный граф можно реализовать как многогранник. ^[5] ${\displaystyle K_{4}}$ ${\displaystyle K_{4}}$

Более поздняя работа Епифанова усилила доказательство Стейница о том, что любой многогранный граф можно свести к ΔY- и YΔ-преобразованиям. Епифанов доказал, что если в плоском графе указаны две вершины, то граф можно свести к одному ребру между этими терминалами, комбинируя ΔY- и YΔ-преобразования с последовательно-параллельными сокращениями . ^[10] Доказательство Епифанова было сложным и неконструктивным, но Трумпер упростил его с помощью методов, основанных на минорах графов . Трумпер заметил, что каждый сеточный граф можно сократить с помощью ΔY- и YΔ-преобразований таким образом, что эта сводимость сохраняется минорами графа и что каждый планарный граф является минором сеточного графа. ^[11] Эту идею можно использовать для замены леммы Стейница о существовании редукционной последовательности. После этой замены остальную часть доказательства можно провести по индукции так же, как исходное доказательство Стейница. ^[8] Для этих доказательств, проводимых с использованием любого из способов нахождения последовательностей ΔY- и YΔ-преобразований, существуют полиэдральные графы, требующие нелинейного числа шагов. Точнее, каждый планарный граф можно сократить, используя число шагов, не более чем пропорциональное , а для бесконечного числа графов требуется число шагов, по крайней мере пропорциональное , где - число вершин в графе. ^{[12] [13]} ${\displaystyle K_{4}}$ ${\displaystyle n^{3/2}}$ ${\displaystyle n^{3/2}}$ ${\displaystyle n}$

Альтернативная форма индукционного доказательства основана на удалении ребер (и сжатии вершин второй степени, которые могут остаться после этого удаления) или сжатии ребер и формировании минора данного плоского графа. Любой многогранный граф можно свести к линейному числу этих операций, и снова операции можно повернуть вспять, а обратные операции выполнить геометрически, что дает многогранную реализацию графа. Однако, хотя доказать, что последовательность редукции существует для этого типа аргумента, проще, и последовательности редукции короче, геометрические шаги, необходимые для обращения последовательности, более сложны. ^[14] ${\displaystyle K_{4}}$

Лифтинг

Если граф нарисован на плоскости с прямыми ребрами, то равновесное напряжение определяется как присвоение ребрам ненулевых действительных чисел (весов) со свойством, что каждая вершина находится в положении, заданном средневзвешенным значением ее вершин. соседи. Согласно соответствию Максвелла–Кремоны, равновесное напряжение можно поднять на кусочно-линейную сплошную трехмерную поверхность такую, что края, образующие границы между плоскими частями поверхности, выступают на заданный рисунок. Вес и длина каждого ребра определяют разницу в наклонах поверхности по обе стороны от ребра, и условие, что каждая вершина находится в равновесии со своими соседями, эквивалентно условию, что эти различия в наклоне заставляют поверхность встречаться с себя правильно в окрестности вершины. Положительные веса переводятся в выпуклые двугранные углы между двумя гранями кусочно-линейной поверхности, а отрицательные веса переводятся в вогнутые двугранные углы. И наоборот, каждая непрерывная кусочно-линейная поверхность возникает таким образом из равновесного напряжения. Если нарисован конечный плоский граф и задано равновесное напряжение таким образом, что все внутренние ребра рисунка имеют положительные веса, а все внешние ребра имеют отрицательные веса, то, переведя это напряжение на трехмерную поверхность таким образом, а затем заменив плоскую поверхность, представляющую внешнюю часть графа, его дополнением в той же плоскости, можно получить выпуклый многогранник с дополнительным свойством, состоящим в том, что его перпендикулярная проекция на плоскость не имеет пересечений. ^{[15] [16]}

Соответствие Максвелла-Кремоны использовалось для получения многогранных реализаций многогранных графов путем объединения его с методом рисования планарных графов WT Tutte , вложением Tutte . Метод Тутте начинается с фиксации одной грани многогранного графа в выпуклом положении на плоскости. Эта грань станет внешней грань рисунка графика. Продолжается метод составлением системы линейных уравнений в координатах вершин, согласно которой каждая оставшаяся вершина должна быть помещена в среднее значение ее соседей. Тогда, как показал Тутте, эта система уравнений будет иметь единственное решение, в котором каждая грань графа изображается в виде выпуклого многоугольника. ^[17] Интуитивно это решение описывает структуру, которая будет получена, если заменить внутренние ребра графа идеальными пружинами и позволить им прийти в состояние с минимальной энергией. ^[18] Результатом является почти равновесное напряжение: если каждому внутреннему ребру присвоить вес один, то каждая внутренняя вершина рисунка будет находиться в равновесии. Однако не всегда возможно присвоить внешним ребрам отрицательные числа, чтобы они тоже находились в равновесии. Такое присвоение всегда возможно, если внешняя грань представляет собой треугольник, поэтому этот метод можно использовать для реализации любого многогранного графа, имеющего треугольную грань. Если многогранный граф не содержит треугольной грани, его двойственный граф содержит треугольник и также является многогранником, поэтому можно реализовать двойственный граф таким образом, а затем реализовать исходный граф как полярный многогранник двойственной реализации. ^{[4] [19]} Альтернативный метод реализации многогранников с использованием подъемов позволяет избежать двойственности, выбирая любую грань с не более чем пятью вершинами в качестве внешней грани. У каждого многогранного графа есть такая грань, и, более тщательно выбирая фиксированную форму этой грани, можно устранить вложение Тутте остальной части графа. ^[20]

Упаковка круга

Многогранник, полученный из круга, уложенного на синюю среднюю сферу. Каждая вершина многогранника представлена ​​в упаковке кружком горизонта (красным). Каждое лицо представлено кругом, образованным его пересечением со сферой.

Согласно одному варианту теоремы об упаковке кругов , для каждого многогранного графа существует система окружностей на плоскости или на любой сфере, представляющая вершины и грани графа, так что:

• каждые две соседние вершины графа изображаются касательными окружностями ,
• каждые две соседние грани графа представлены касательной окружностью,
• каждая пара вершины и грани, которой она касается, представлена ​​кругами, пересекающимися под прямым углом , и
• все остальные пары кругов отделены друг от друга. ^[21]

Та же система кругов образует представление двойственного графа, меняя ролями круги, представляющие вершины, и круги, представляющие грани. Из любого такого представления на сфере, вложенной в трехмерное евклидово пространство, можно сформировать выпуклый многогранник, комбинаторно эквивалентный заданному графу, как пересечение полупространств, границы которых проходят через окружности граней. Из каждой вершины этого многогранника горизонт сферы, видимый из этой вершины, представляет собой круг, который ее представляет. Это свойство горизонта определяет трехмерное положение каждой вершины, и многогранник можно эквивалентно определить как выпуклую оболочку вершин, расположенных таким образом. Сфера становится средней сферой реализации: каждое ребро многогранника касается сферы в точке, где две касательные окружности вершин пересекают две касательные окружности граней. ^[22]

Реализации с дополнительными свойствами

Целочисленные координаты

Можно доказать более сильную форму теоремы Стейница, что любой многогранный граф может быть реализован выпуклым многогранником, координаты которого являются целыми числами . ^[23] Например, таким образом можно усилить оригинальное доказательство Стейница, основанное на индукции. Однако целые числа, полученные в результате конструкции Стейница, являются дважды экспоненциальными по числу вершин данного многогранного графа. Запись чисел такой величины в двоичной записи потребовала бы экспоненциального числа битов. ^[19] Геометрически это означает, что некоторые элементы многогранника могут иметь размер в два раза экспоненциально больший, чем другие, что делает реализации, полученные с помощью этого метода, проблематичными для приложений при рисовании графов . ^[4]

Последующие исследователи нашли алгоритмы реализации, основанные на подъеме, которые используют только линейное количество бит на вершину. ^{[20] [24]} Также можно ослабить требование, чтобы координаты были целыми числами, и назначить координаты таким образом, чтобы -координаты вершин были различными целыми числами в диапазоне от 0 до, а две другие координаты были действительными. числа в единичном интервале так, чтобы каждое ребро имело длину не менее единицы, а весь многогранник имел линейный объем. ^{[25] [26]} Известно, что некоторые многогранные графы можно реализовать на сетках только полиномиального размера; в частности, это верно для пирамид (реализаций колесных графов ), призм (реализаций призменных графов ) и сложенных многогранников (реализаций аполлоновых сетей ). ^[27] ${\displaystyle x}$ ${\displaystyle 2n-4}$

Другой способ констатировать существование целочисленных реализаций состоит в том, что каждый трехмерный выпуклый многогранник имеет комбинаторно эквивалентный целочисленный многогранник. ^[23] Например, правильный додекаэдр сам по себе не является целочисленным многогранником из-за своих правильных пятиугольных граней, но его можно реализовать как эквивалентный целочисленный пиритоэдр . ^[20] Это не всегда возможно в более высоких измерениях, где существуют многогранники (например, построенные на основе конфигурации Перля ), которые не имеют целочисленного эквивалента. ^[28]

Равные уклоны

Граф Халина — это частный случай многогранного графа, образованного из планарно-вложенного дерева (без вершин второй степени) путем соединения листьев дерева в цикл . Для графов Халина можно выбрать многогранные реализации особого типа: внешний цикл образует горизонтальную выпуклую базовую грань, а каждая вторая грань лежит непосредственно над базовой гранью (как в многогранниках, реализованных подъемом), причем все эти верхние грани имеющие одинаковый наклон. Многогранные поверхности с гранями одинакового наклона над любым базовым многоугольником (не обязательно выпуклым) могут быть построены из прямого скелета многоугольника , и эквивалентный способ описания этой реализации состоит в том, что двумерная проекция дерева на базовую грань образует его прямую поверхность. скелет. Для доказательства этого результата используется индукция: любое корневое дерево можно свести к меньшему дереву, удалив листья из внутреннего узла, все дочерние элементы которого являются листьями, граф Халина, сформированный из меньшего дерева, реализуется по гипотезе индукции, и это можно изменить эту реализацию, чтобы добавить любое количество дочерних листьев к узлу дерева, чьи дочерние элементы были удалены. ^[29]

Уточняем форму лица

В любом многограннике, представляющем данный многогранный граф , грани — это именно те циклы , в которых не разделяются на две компоненты: то есть удаление лицевого цикла из оставшейся части оставляет в виде связного подграфа. Такие циклы называются периферическими циклами . Таким образом, комбинаторная структура граней (но не их геометрические формы) однозначно определяется из структуры графа. Другое усиление теоремы Стейница, предложенное Барнеттом и Грюнбаумом, утверждает, что для любого многогранного графа, любой грани графа и любого выпуклого многоугольника, представляющего эту грань, можно найти многогранную реализацию всего графа, которая имеет заданную форму для обозначенное лицо. Это связано с теоремой Тутте о том, что любой многогранный граф можно нарисовать на плоскости со всеми выпуклыми гранями и любой заданной формой его внешней грани. Однако рисунки плоских графов , полученные методом Тутте, не обязательно переходят в выпуклые многогранники. Вместо этого Барнетт и Грюнбаум доказывают этот результат, используя индуктивный метод. ^[30] Также всегда возможно, учитывая многогранный граф и произвольный цикл в , найти реализацию, для которой образует силуэт реализации при параллельном проецировании . ^[31] ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle C}$ ${\displaystyle G}$ ${\displaystyle C}$

Касательные сферы

Реализация многогранников с использованием теоремы об упаковке кругов обеспечивает еще одно усиление теоремы Стейница: каждый трехсвязный плоский граф можно представить как выпуклый многогранник таким образом, что все его ребра касаются одной и той же единичной сферы , средней сферы многогранник. ^[22] Выполняя тщательно выбранное преобразование Мёбиуса упаковки кругов перед преобразованием ее в многогранник, можно найти многогранную реализацию, которая реализует все симметрии основного графа в том смысле, что каждый автоморфизм графа является симметрией полиэдральная реализация. ^{[32] [33]} В более общем смысле, если это многогранный граф и любое гладкое трехмерное выпуклое тело , можно найти многогранное представление, в котором все ребра касаются . ^[34] ${\displaystyle G}$ ${\displaystyle K}$ ${\displaystyle G}$ ${\displaystyle K}$

Методы упаковки кругов также можно использовать для характеристики графов многогранников, у которых есть описанная сфера , проходящая через все вершины, или сфера, касающаяся всех их граней. (Многогранники с описанной сферой также важны в гиперболической геометрии как идеальные многогранники .) В обоих случаях существование сферы эквивалентно разрешимости системы линейных неравенств о положительных действительных переменных, связанных с каждым ребром графа. В случае сферы сумма этих переменных должна равняться ровно одной в каждом цикле граней графа и более одной в каждом цикле, не являющемся гранью. Двойственно, для описанной сферы переменные должны в сумме давать единицу в каждой вершине и более одной в каждом разрезе с двумя или более вершинами на каждой стороне разреза. Хотя может потребоваться экспоненциально много линейных неравенств, решение (если оно существует) может быть найдено за полиномиальное время, используя метод эллипсоида . Значения переменных из решения определяют углы между парами окружностей в упаковке кругов, соответствующий многогранник которых имеет заданное отношение к своей сфере. ^{[35] [36]}

Связанные результаты

Графы трехмерных невыпуклых многогранников могут быть несвязными (слева), и даже для топологически сферических многогранников, грани которых представляют собой простые многоугольники, эти графы могут быть несвязными (справа). ^[37]

В любой размерности выше трех алгоритмическая задача Стейница состоит в определении того, является ли данная решетка решеткой граней выпуклого многогранника . Маловероятно, что он будет иметь полиномиальную временную сложность, поскольку он NP-труден и более полен для экзистенциальной теории действительных чисел , даже для четырехмерных многогранников, согласно теореме об универсальности Рихтера-Геберта. ^[38] Здесь экзистенциальная теория действительных чисел представляет собой класс вычислительных задач, которые могут быть сформулированы в терминах поиска реальных переменных, удовлетворяющих заданной системе полиномиальных уравнений и неравенств. Для алгоритмической задачи Стейница переменными такой задачи могут быть координаты вершин многогранника, а уравнения и неравенства могут использоваться для задания плоскостности каждой грани в заданной решетке граней и выпуклости каждого угла между гранями. Полнота означает, что любая другая проблема в этом классе может быть преобразована в эквивалентный экземпляр алгоритмической задачи Стейница за полиномиальное время. Существование такого преобразования означает, что если алгоритмическая задача Стейница имеет полиномиальное решение по времени, то то же самое имеет и каждая проблема экзистенциальной теории действительных чисел и каждая проблема в NP. ^[39] Однако, поскольку данный граф может соответствовать более чем одной решетке граней, трудно распространить этот результат о полноте на проблему распознавания графов 4-многогранников. Определение вычислительной сложности этой задачи распознавания графов остается открытым. ^[40]

Исследователи также нашли теоретико-графовые характеристики графиков некоторых специальных классов трехмерных невыпуклых многогранников ^{[37] [41]} и четырехмерных выпуклых многогранников. ^{[40] [42] [43]} Однако в обоих случаях общая проблема остается нерешенной. Действительно, даже проблема определения того, какие полные графы являются графами невыпуклых многогранников (кроме тетраэдра и многогранника Часара ), остается нерешенной. ^[44] ${\displaystyle K_{4}}$ ${\displaystyle K_{7}}$

Теорема Эберхарда частично характеризует мультимножества многоугольников , которые можно объединить в грани выпуклого многогранника. Это можно доказать, сформировав 3-связный плоский граф с заданным набором граней многоугольника, а затем применив теорему Стейница, чтобы найти многогранную реализацию этого графа. ^[3]

Ласло Ловас показал соответствие между многогранными представлениями графов и матрицами, реализующими графовые инварианты Колена де Вердьера тех же графов. Инвариант Колена де Вердьера — это максимальный коранг взвешенной матрицы смежности графа при некоторых дополнительных условиях, которые не имеют значения для многогранных графов. Это квадратные симметричные матрицы, индексированные по вершинам, с весом вершины в диагональном коэффициенте и с весом ребра в недиагональных коэффициентах и ​​. Когда вершины и не являются соседними, коэффициент должен быть равен нулю. Этот инвариант не превосходит трех тогда и только тогда, когда граф является плоским . Как показывает Ловас, когда граф является многогранником, его представление в виде многогранника можно получить, найдя взвешенную матрицу смежности коранга три, найдя три вектора, образующие основу его нулевого пространства , используя коэффициенты этих векторов в качестве координат для вершины многогранника и соответствующее масштабирование этих вершин. ^[45] ${\displaystyle i}$ ${\displaystyle M_{i,i}}$ ${\displaystyle i,j}$ ${\displaystyle M_{i,j}}$ ${\displaystyle M_{j,i}}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle M_{i,j}}$

История

История теоремы Стейница описана Грюнбаумом (2007), ^[46] который отмечает ее первое появление в загадочной форме в публикации Эрнста Стейница , первоначально написанной в 1916 году. ^[6] Стейниц предоставил более подробную информацию в более поздних конспектах лекций, опубликованных после его смерти в 1928 г. Хотя современные трактовки теоремы Стейница утверждают, что она представляет собой теоретико-графовую характеристику многогранников, Стейниц не использовал язык графов. ^[46] Теоретико-графовая формулировка теоремы была введена в начале 1960-х годов Бранко Грюнбаумом и Теодором Моцкиным , а ее доказательство также было преобразовано в теорию графов в тексте Грюнбаума 1967 года «Выпуклые многогранники» . ^[46] Работа Епифанова по ΔY- и YΔ-преобразованиям , усиливающая доказательство Стейница, была мотивирована иными проблемами, чем характеризация многогранников. Трумпер (1989) благодарит Грюнбаума за то, что он заметил актуальность этой работы для теоремы Стейница. ^[11]

Соответствие Максвелла-Кремоны между диаграммами напряжений и многогранными подъемами было развито в серии статей Джеймса Клерка Максвелла с 1864 по 1870 год на основе более ранних работ Пьера Вариньона , Уильяма Рэнкина и других и было популяризировано в конце 19 века Луиджи Кремона . ^[47] Наблюдение о том, что это соответствие можно использовать с вложением Тутте для доказательства теоремы Стейница, взято из Eades & Garvan (1995); ^[4] см. также Рихтер-Геберт (1996). ^[38]

Теорема об упаковке кругов была доказана Полом Кёбе в 1936 г. ^{[48] [49]} и (независимо) Е. М. Андреевым в 1970 г.; ^{[49] [50]} он был популяризирован в середине 1980-х годов Уильямом Терстоном , которого (несмотря на цитирование Кебе и Андреева) часто называют одним из его первооткрывателей. ^[49] Версия теоремы Андреева уже была сформулирована как характеристика типа Стейница для некоторых многогранников в гиперболическом пространстве , ^[50] а использование упаковки кругов для реализации многогранников со средними сферами взято из работы Терстона. ^[51] Проблема характеристики многогранников с вписанными или описанными сферами, в конечном итоге решенная с использованием метода, основанного на реализации упаковки кругов, восходит к неопубликованной работе Рене Декарта около 1630 года ^[52] и Якоба Штайнера в 1832 году; ^{[35] [53]} первые примеры многогранников, не имеющих реализации с описанной или внутренней сферой, были даны Стейницем в 1928 году. ^{[35] [54]}

Рекомендации

1. Вайсштейн, Эрик В. , «Многогранный граф», MathWorld
2. Штурмфельс, Бернд (1987), «Граничные комплексы выпуклых многогранников не могут быть охарактеризованы локально», Журнал Лондонского математического общества , Вторая серия, 35 (2): 314–326, CiteSeerX 10.1.1.106.3222 , doi : 10.1112/ жлмс/с2-35.2.314, МР  0881520 
3. Малкевич, Джозеф, «Методы доказательства комбинаторных теорем о 3-многогранниках», Геометрические структуры (конспекты курса) , Городской университет Нью-Йорка
4. Идс, Питер ; Гарван, Патрик (1995), «Рисование плоских напряженных графов в трех измерениях», в Бранденбурге, Франц-Йозеф (редактор), Рисование графиков, Симпозиум по рисованию графов, GD '95, Пассау, Германия, 20-22 сентября 1995 г. , Труды , Конспекты лекций по информатике , вып. 1027, Springer, стр. 212–223, doi : 10.1007/BFb0021805 , MR  1400675.
5. Грюнбаум, Бранко (2003), «13.1 Теорема Стейница», Выпуклые многогранники , Тексты для выпускников по математике , том. 221 (2-е изд.), Springer-Verlag, стр. 235–244, ISBN. 0-387-40409-0
6. Стейниц, Эрнст (1922), «IIIAB12: Polyeder und Raumeinteilungen», Encyclopädie der mathematischen Wissenschaften (на немецком языке), vol. Группа 3 (Геометрия), стр. 1–139, Abgeschlossen, 31 августа 1916 г.
7. С технической точки зрения этот граф представляет собой 1-скелет; см. Грюнбаум (2003), с. 138 и Зиглер (1995), с. 64.
8. Циглер, Гюнтер М. (1995), «Глава 4: Теорема Стейница для 3-многогранников», Лекции по многогранникам , Тексты для аспирантов по математике , vol. 152, Springer-Verlag, стр. 103–126, ISBN. 0-387-94365-Х
9. Балинский, ML (1961), «О графической структуре выпуклых многогранников в n-пространстве», Pacific Journal of Mathematics , 11 (2): 431–434, doi : 10.2140/pjm.1961.11.431 , MR  0126765
10. Епифанов, Г. В. (1966), "Приведение плоского графа к ребру преобразованиями звезда-треугольник", Доклады Академии наук СССР , 166 : 19–22, MR  0201337, Zbl  0149.21301
11. Трумпер, К. (1989), «О сокращении дельта-вай для плоских графов», Journal of Graph Theory , 13 (2): 141–148, doi : 10.1002/jgt.3190130202, MR  0994737
12. Арангури, Сантьяго; Чанг, Сянь-Чжи; Фридман, Дилан (2022), «Распутывание плоских графиков и кривых, оставаясь позитивными», Труды ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA) 2022 года , SIAM, стр. 211–225, doi : 10.1137/1.9781611977073.11, МР  4415048, S2CID  245778178
13. Чанг, Сянь-Чжи; Эриксон, Джефф (2017), «Распутывание плоских кривых», Дискретная и вычислительная геометрия , 58 (4): 889–920, arXiv : 1702.00146 , doi : 10.1007/s00454-017-9907-6, MR  3717242, S2CID  254027198
14. Барнетт, Дэвид В.; Грюнбаум, Бранко (1969), «О теореме Стейница о выпуклых 3-многогранниках и о некоторых свойствах плоских графов», в Chartrand, G .; Капур, С.Ф. (ред.), « Множество граней теории графов: материалы конференции, состоявшейся в Университете Западного Мичигана, Каламазу, Мичиган, 31 октября - 2 ноября 1968 г.» , Конспекты лекций по математике , том. 110, Springer, стр. 27–40, номер документа : 10.1007/BFb0060102, MR  0250916.
15. Максвелл, Дж. Клерк (1864), «О обратных фигурах и диаграммах сил», Philosophical Magazine , 4-я серия, 27 (182): 250–261, doi : 10.1080/14786446408643663
16. Уайтли, Уолтер (1982), «Движения и напряжения проецируемых многогранников», Структурная топология , 7 : 13–38, hdl : 2099/989, MR  0721947
17. Тутте, WT (1963), «Как нарисовать график», Труды Лондонского математического общества , 13 : 743–767, doi : 10.1112/plms/s3-13.1.743, MR  0158387
18. Брандес, Ульрик (2001), «Опираясь на физические аналогии», Кауфманн, Майкл; Вагнер, Доротея (ред.), Рисование графиков: методы и модели , Конспекты лекций по информатике , том. 2025, Берлин: Springer, стр. 71–86, CiteSeerX 10.1.1.9.5023 , doi : 10.1007/3-540-44969-8_4, MR  1880146. 
19. Онн, Шмуэль; Штурмфельс, Бернд (1994), «Количественная теорема Стейница», Beiträge zur Algebra und Geometrie , 35 (1): 125–129, MR  1287206
20. Рибо Мор, Арес; Роте, Гюнтер; Шульц, Андре (2011), «Вложения 3-многогранников в мелкую сетку», Дискретная и вычислительная геометрия , 45 (1): 65–87, arXiv : 0908.0488 , doi : 10.1007/s00454-010-9301-0, MR  2765520, S2CID  10141034
21. Брайтуэлл, Грэм Р .; Шайнерман, Эдвард Р. (1993), «Представления плоских графов», SIAM Journal on Discrete Mathematics , 6 (2): 214–229, doi : 10.1137/0406017, MR  1215229
22. Циглер, Гюнтер М. (2007), «Выпуклые многогранники: экстремальные конструкции и f -векторные формы. Раздел 1.3: Теорема Стейница через упаковки кругов», Миллер, Эзра; Райнер, Виктор; Штурмфельс, Бернд (ред.), Геометрическая комбинаторика , Серия IAS / Park City Mathematics, том. 13, Американское математическое общество , стр. 628–642, ISBN. 978-0-8218-3736-8
23. Grünbaum (2003), теорема 13.2.3, с. 244, утверждает это в эквивалентной форме, где координаты являются рациональными числами .
24. Бучин, Кевин; Шульц, Андре (2010), «О количестве остовных деревьев, которые может иметь плоский граф», де Берг, Марк ; Мейер, Ульрих (ред.), Алгоритмы - ESA 2010, 18-й ежегодный европейский симпозиум, Ливерпуль, Великобритания, 6-8 сентября 2010 г., Материалы, Часть I , Конспекты лекций по информатике , том. 6346, Springer, стр. 110–121, CiteSeerX 10.1.1.746.942 , doi : 10.1007/978-3-642-15775-2_10, ISBN  978-3-642-15774-5, МР  2762847, S2CID  42211547
25. Хробак, Марек; Гудрич, Майкл Т .; Тамассиа, Роберто (1996), «Выпуклые рисунки графиков в двух и трех измерениях», Труды 12-го симпозиума ACM по вычислительной геометрии (SoCG '96) , ACM, стр. 319–328, doi : 10.1145/237218.237401, S2CID  1015103
26. Шульц, Андре (2011), «Рисование 3-многогранников с хорошим разрешением вершин», Журнал графовых алгоритмов и приложений , 15 (1): 33–52, doi : 10.7155/jgaa.00216 , MR  2776000
27. Демейн, Эрик Д .; Шульц, Андре (2017), «Вложение сложенных многогранников в сетку полиномиального размера», Discrete & Computational Geometry , 57 (4): 782–809, arXiv : 1403.7980 , doi : 10.1007/s00454-017-9887-6, MR  3639604, S2CID  104867
28. Грюнбаум (2003), с. 96а.
29. Айххольцер, Освин; Ченг, Ховард; Девадосс, Сатьян Л. ; Хакл, Томас; Хубер, Стефан; Ли, Брайан; Ристески, Андрей (2012), «Что делает дерево прямым скелетом?» (PDF) , Материалы 24-й Канадской конференции по вычислительной геометрии (CCCG'12)
30. Барнетт, Дэвид В.; Грюнбаум, Бранко (1970), «Предварительное задание формы лица», Pacific Journal of Mathematics , 32 (2): 299–306, doi : 10.2140/pjm.1970.32.299 , MR  0259744
31. Барнетт, Дэвид В. (1970), «Проекции 3-многогранников», Израильский журнал математики , 8 (3): 304–308, doi : 10.1007/BF02771563, MR  0262923, S2CID  120791830
32. Харт, Джордж В. (1997), «Вычисление канонических многогранников», Mathematica в образовании и исследованиях , 6 (3): 5–10
33. Берн, Маршалл В.; Эппштейн, Дэвид (2001), «Оптимальные преобразования Мёбиуса для визуализации информации и создания сеток», Дене, Франк КХА; Зак, Йорг-Рюдигер; Тамассиа, Роберто (ред.), «Алгоритмы и структуры данных», 7-й международный семинар, WADS 2001, Провиденс, Род-Айленд, США, 8–10 августа 2001 г., Материалы , конспекты лекций по информатике , том. 2125, Springer, стр. 14–25, arXiv : cs/0101006 , doi : 10.1007/3-540-44634-6_3, S2CID  3266233
34. Шрамм, Одед (1992), «Как поместить яйцо в клетку», Inventiones Mathematicae , 107 (3): 543–560, Bibcode : 1992InMat.107..543S, doi : 10.1007/BF01231901, MR  1150601, S2CID  189830473
35. Ривин, Игорь (1996), «Характеристика идеальных многогранников в гиперболическом трехмерном пространстве», Annals of Mathematics , Second Series, 143 (1): 51–70, doi : 10.2307/2118652, JSTOR  2118652, MR  1370757
36. Дилленкур, Майкл Б.; Смит, Уоррен Д. (1996), «Теоретико-графовые условия вписываемости и реализуемости Делоне», Discrete Mathematics , 161 (1–3): 63–77, doi :10.1016/0012-365X(95)00276-3, MR  1420521, S2CID  16382428
37. Эппштейн, Дэвид ; Мамфорд, Елена (2014), «Теоремы Стейница для простых ортогональных многогранников», Журнал вычислительной геометрии , 5 (1): 179–244, doi : 10.20382/jocg.v5i1a10, MR  3259910, S2CID  8531578
38. Рихтер-Геберт, Юрген (1996), Пространства реализации многогранников , Конспекты лекций по математике , том. 1643, Springer-Verlag, CiteSeerX 10.1.1.2.3495 , doi : 10.1007/BFb0093761, ISBN  978-3-540-62084-6, МР  1482230
39. Шефер, Маркус (2013), «Реализуемость графов и связей», в Пах, Янош (редактор), «Тридцать эссе по геометрической теории графов» , Нью-Йорк: Springer, стр. 461–482, doi : 10.1007/978-1 -4614-0110-0_24, МР  3205168
40. Эппштейн, Дэвид (2020), «Древовидные вершины и их графики», Дискретная и вычислительная геометрия , 64 (2): 259–289, arXiv : 1510.03152 , doi : 10.1007/s00454-020-00177-0, MR  4131546, S2CID  213885326
41. Хон, Сок Хи ; Нагамоти, Хироши (2011), «Распространение теоремы Стейница на восходящие звездчатые многогранники и сферические многогранники», Algorithmica , 61 (4): 1022–1076, doi : 10.1007/s00453-011-9570-x, MR  2852056, S2CID  12622357
42. Слепой, Розвита ; Мани-Левитска, Питер (1987), «Загадки и изоморфизмы многогранников», Aequationes Mathematicae , 34 (2–3): 287–297, doi : 10.1007/BF01830678, MR  0921106, S2CID  120222616
43. Калаи, Гил (1988), «Простой способ отличить простой многогранник по его графику», Журнал комбинаторной теории , серия A, 49 (2): 381–383, doi : 10.1016/0097-3165(88)90064 -7 , МР  0964396
44. Циглер, Гюнтер М. (2008), «Многогранные поверхности высокого рода», Дискретная дифференциальная геометрия , Семинары в Обервольфахе, том. 38, Springer, стр. 191–213, arXiv : math/0412093 , doi : 10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7, МР  2405667, S2CID  15911143
45. Ловас, Ласло (2001), «Представления Стейница многогранников и число Колина де Вердьера», Журнал комбинаторной теории , серия B, 82 (2): 223–236, doi : 10.1006/jctb.2000.2027 , MR  1842113
46. Грюнбаум, Бранко (2007), «Графики многогранников; многогранники как графы», Discrete Mathematics , 307 (3–5): 445–463, doi : 10.1016/j.disc.2005.09.037, hdl : 1773/2276 , МР  2287486
47. Эриксон, Джефф; Лин, Патрик (2020), «Тороидальная переписка Максвелла-Кремоны-Делоне», в Кабельо, Серджио; Чен, Дэнни З. (ред.), 36-й Международный симпозиум по вычислительной геометрии (SoCG 2020) , Международные труды Лейбница по информатике (LIPIcs), том. 164, Дагштуль, Германия: Schloss Dagstuhl–Leibniz-Zentrum für Informatik, стр. 40:1–40:17, arXiv : 2003.10057 , doi :10.4230/LIPIcs.SoCG.2020.40, ISBN 978-3-95977-143-6, S2CID  209514295
48. Кёбе, Пауль (1936), «Kontaktprobleme der Konformen Abbildung», Berichte über die Verhandlungen der Sächsischen Akademie der Wissenschaften zu Leipzig: Mathematisch-Physische Klasse (на немецком языке), 88 : 141–164
49. Стивенсон, Кеннет (2003), «Упаковка кругов: математическая сказка» (PDF) , Уведомления Американского математического общества , 50 (11): 1376–1388, CiteSeerX 10.1.1.101.5592 , MR  2011604 
50. Андреев, Е. М. (1970), «Выпуклые многогранники в пространствах Лобачевского», Математический сборник , 81 (123): 445–478, Бибкод : 1970SbMat..10..413A, doi : 10.1070/SM1970v010n03ABEH001677, MR  025 9734
51. Шрамм, Одед (1991), «Существование и уникальность упаковок с заданной комбинаторикой», Израильский журнал математики , 73 (3): 321–341, doi : 10.1007/BF02773845, MR  1135221, S2CID  121855202; см. обсуждение после следствия 3.8, с. 329
52. Федерико, Паскуале Джозеф (1982), Декарт о многогранниках: исследование «De Solidorum elementis» , Источники по истории математики и физических наук, том. 4, Спрингер, с. 52
53. Штайнер, Якоб (1832), «Вопрос 77», Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander (на немецком языке), Берлин: G. Fincke, стр. 316
54. Стейниц, Эрнст (1928), «Über изопериметрические проблемы bei konvexen Polyedern», Journal für die Reine und Angewandte Mathematik (на немецком языке), 1928 (159): 133–143, doi : 10.1515/crll.1928.159.133, MR  1581158 , S2CID  199546274