Кадемлия

Структура данных на основе хэша

Kademlia — это распределенная хеш-таблица для децентрализованных одноранговых компьютерных сетей, разработанная Петаром Маймунковым и Дэвидом Мазьером в 2002 году. ^{[1] [2]} Она определяет структуру сети и обмен информацией посредством поиска узлов . Узлы Kademlia взаимодействуют между собой с помощью UDP . Узлы-участники формируют виртуальную или оверлейную сеть . Каждый узел идентифицируется номером или идентификатором узла . Идентификатор узла служит не только для идентификации, но алгоритм Kademlia использует идентификатор узла для поиска значений (обычно хэшей файлов или ключевых слов).

Чтобы найти значение, связанное с заданным ключом, алгоритм исследует сеть в несколько шагов. На каждом шаге будут найдены узлы, которые находятся ближе к ключу, пока контактируемый узел не вернет значение или пока не будут найдены более близкие узлы. Это очень эффективно: как и многие другие DHT , Kademlia контактирует только с узлами во время поиска из общего числа узлов в системе. ${\displaystyle O(\log n)}$ ${\displaystyle n}$

Дополнительные преимущества обнаруживаются, в частности, в децентрализованной структуре, которая повышает устойчивость к атакам типа «отказ в обслуживании» . Даже если будет затоплен целый набор узлов, это окажет ограниченное влияние на доступность сети, поскольку сеть восстановится сама, связав сеть вокруг этих «дыр».

Реализация Kademlia в I2P изменена для смягчения уязвимостей Kademlia, таких как атаки Сивиллы . ^[3]

Подробности системы

Одноранговые сети по своей сути состоят из узлов. Протоколы, которые эти узлы используют для связи и поиска информации, со временем стали более эффективными. Файлообменные сети первого поколения, такие как Napster , полагались на центральную базу данных для координации поиска в сети. Одноранговые сети второго поколения, такие как Gnutella , использовали лавинную рассылку для поиска файлов, выполняя поиск по каждому узлу в сети. Одноранговые сети третьего поколения, такие как Bittorrent , используют распределенные хеш-таблицы для поиска файлов в сети. Распределенные хеш-таблицы хранят местоположения ресурсов по всей сети.

Kademlia использует расчет «расстояния» между двумя узлами. Это расстояние вычисляется как исключающее ИЛИ (XOR) двух идентификаторов узлов, принимая результат как беззнаковое целое число . Ключи и идентификаторы узлов имеют одинаковый формат и длину, поэтому расстояние между ними можно вычислить точно так же. Идентификатор узла обычно представляет собой большое случайное число, которое выбирается с целью быть уникальным для конкретного узла (см. UUID ). Может и случается, что географически далекие узлы — например, из Германии и Австралии — могут быть «соседями», если они выбрали похожие случайные идентификаторы узлов.

XOR был выбран, потому что он действует как функция расстояния между всеми идентификаторами узлов. А именно:

• расстояние между узлом и самим собой равно нулю
• он симметричен: «расстояния», рассчитанные от А до В и от В до А, одинаковы
• это следует из неравенства треугольника : если A, B и C являются вершинами (точками) треугольника, то расстояние от A до B меньше (или равно) суммы расстояния от A до C и расстояния от C до B.

Этих трех условий достаточно, чтобы гарантировать, что XOR охватывает все основные, важные особенности «реальной» функции расстояния, будучи при этом дешевым и простым в вычислении. ^[1]

Каждая итерация поиска Kademlia приближает нас к цели на один бит. Базовый алгоритм поиска Kademlia имеет сложность O(log ₂  (n)) , что означает, что для сети с узлами потребуется максимум шагов, чтобы найти этот узел. ${\textstyle 2^{n}}$ ${\displaystyle n}$

Таблицы маршрутизации фиксированного размера

Таблицы маршрутизации фиксированного размера были представлены в предварительной версии оригинальной статьи ^[4] и используются в более поздней версии только для некоторых математических доказательств. Фактическая реализация Kademlia не имеет таблицы маршрутизации фиксированного размера, а имеет динамический размер.

Таблицы маршрутизации Kademlia состоят из списка для каждого бита идентификатора узла (например, если идентификатор узла состоит из 128 бит, узел будет хранить 128 таких списков .) Каждая запись в списке содержит необходимые данные для определения местоположения другого узла. Данные в каждой записи списка обычно представляют собой IP-адрес , порт и идентификатор узла другого узла. Каждый список соответствует определенному расстоянию от узла. Узлы, которые могут быть включены в n- ^й список , должны иметь отличающийся n- ^й бит от идентификатора узла; первые n-1 битов идентификатора кандидата должны совпадать с битами идентификатора узла. Это означает, что очень легко заполнить первый список , поскольку 1/2 узлов в сети являются далекими кандидатами. Следующий список может использовать только 1/4 узлов в сети (на один бит ближе, чем первый) и т. д.

При использовании идентификатора длиной 128 бит каждый узел в сети будет классифицировать другие узлы по одному из 128 различных расстояний, по одному конкретному расстоянию на бит.

По мере того, как узлы встречаются в сети, они добавляются в списки . Это включает в себя операции хранения и извлечения и даже помощь другим узлам в поиске ключа. Каждый обнаруженный узел будет рассматриваться для включения в списки . Поэтому знания, которые узел имеет о сети, очень динамичны. Это позволяет сети постоянно обновляться и повышает устойчивость к сбоям или атакам.

В литературе Kademlia списки называются k-корзинами . k — это системное число, например 20. Каждая k -корзина — это список, содержащий до k записей внутри; т. е. для сети с k=20 каждый узел будет иметь списки, содержащие до 20 узлов для определенного бита (определенного расстояния от себя).

Поскольку возможные узлы для каждого k-bucket быстро уменьшаются (потому что будет очень мало узлов, которые находятся так близко), k-bucket с меньшим битом полностью отобразят все узлы в этой секции сети. Поскольку количество возможных идентификаторов намного больше, чем может быть любая популяция узлов, некоторые из k -bucket, соответствующие очень коротким расстояниям, останутся пустыми.

Раздел сети для узла 110

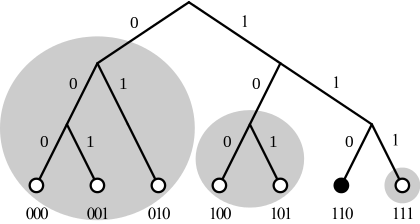
Рассмотрим простую сеть справа. Размер сети составляет 2^3 или восемь максимальных ключей и узлов. Участвуют семь узлов; маленькие кружки внизу. Рассматриваемый узел — это узел шесть (двоичный 110) черного цвета. Для каждого узла в этой сети есть три k-bucket . Узлы нулевой, первый и второй (двоичные 000, 001 и 010) являются кандидатами на самый дальний k-bucket . Узел третий (двоичный 011, не показан) не участвует в сети. В среднем k-bucket размещены узлы четвертый и пятый (двоичные 100 и 101). Наконец, третий k-bucket может содержать только узел семь (двоичный 111). Каждый из трех k-bucket заключен в серый кружок. Если размер k-bucket был два, то самый дальний 2-bucket может содержать только два из трех узлов. Например, если узел шесть имеет узел один и два в самом дальнем 2-ведерном сегменте, ему придется запросить поиск идентификатора узла для этих узлов, чтобы найти местоположение (IP-адрес) узла ноль. Каждый узел хорошо знает свое окружение и имеет контакт с несколькими узлами, находящимися далеко, что может помочь найти другие узлы, находящиеся далеко.

Известно, что узлы, которые долгое время были соединены в сеть, вероятно, останутся соединенными в течение длительного времени в будущем. ^{[5] [6]} Благодаря этому статистическому распределению Kademlia выбирает давно соединенные узлы, которые остаются сохраненными в k-buckets. Это увеличивает количество известных действительных узлов в какой-то момент в будущем и обеспечивает более стабильную сеть.

Когда k-bucket заполнен и для этого k-bucket обнаружен новый узел , последний недавно просмотренный узел в k-bucket пингуется. Если узел оказывается все еще живым, новый узел помещается во вторичный список, кэш замены. Кэш замены используется только в том случае, если узел в k-bucket перестает отвечать. Другими словами: новые узлы используются только тогда, когда старые узлы исчезают.

Протокол сообщений

У Кадемлии четыре сообщения.

• PING — используется для проверки работоспособности узла.
• STORE — Сохраняет пару (ключ, значение) в одном узле.
• FIND_NODE — Получатель запроса вернет k узлов в своих собственных сегментах, которые являются наиболее близкими к запрошенному ключу.
• FIND_VALUE — то же, что и FIND_NODE, но если у получателя запроса есть запрошенный ключ в хранилище, он вернет соответствующее значение.

Каждое сообщение RPC включает случайное значение от инициатора. Это гарантирует, что при получении ответа он будет соответствовать ранее отправленному запросу (см. magic cookie ).

Расположение узлов

Поиск узлов может выполняться асинхронно. Количество одновременных поисков обозначается α и обычно равно трем. Узел инициирует запрос FIND_NODE, запрашивая α узлов в своих собственных k-корзинах , которые являются ближайшими к искомому ключу. Когда эти узлы-получатели получают запрос, они будут искать в своих k-корзинах и возвращать k ближайших узлов к искомому ключу, который они знают. Запрашивающая сторона обновит список результатов полученными результатами (идентификаторами узлов), сохранив k лучших ( k узлов, которые ближе к искомому ключу), которые отвечают на запросы. Затем запрашивающая сторона выберет эти k лучших результатов и отправит им запрос, и будет повторять этот процесс снова и снова. Поскольку каждый узел лучше знает свое окружение, чем любой другой узел, полученными результатами будут другие узлы, которые каждый раз все ближе и ближе к искомому ключу. Итерации продолжаются до тех пор, пока не будут возвращены узлы, которые ближе, чем лучшие предыдущие результаты. Когда итерации останавливаются, лучшими k узлами в списке результатов являются те узлы во всей сети, которые ближе всего к искомому ключу.

Информация об узле может быть дополнена временем кругового обхода или RTT. Эта информация будет использоваться для выбора тайм-аута, специфичного для каждого консультируемого узла. Когда время запроса истекает, может быть инициирован другой запрос, никогда не превышающий α запросов в то же время.

Поиск ресурсов

Информация находится путем сопоставления ее с ключом. Для сопоставления обычно используется хэш . Узлы-хранилища будут иметь информацию из-за предыдущего сообщения STORE. Поиск значения следует той же процедуре, что и поиск ближайших узлов к ключу, за исключением того, что поиск завершается, когда узел имеет запрошенное значение в своем хранилище и возвращает это значение.

Значения хранятся в нескольких узлах (k из них), чтобы узлы могли приходить и уходить, и при этом иметь значение, доступное в каком-то узле. Периодически узел, хранящий значение, будет исследовать сеть, чтобы найти k узлов, которые находятся рядом с ключевым значением, и реплицировать значение на них. Это компенсирует исчезнувшие узлы.

Кроме того, для популярных значений, которые могут иметь много запросов, нагрузка на узлы хранилища уменьшается за счет того, что извлекатель сохраняет это значение в некотором узле рядом, но за пределами k ближайших узлов. Это новое хранилище называется кэшем. Таким образом, значение сохраняется все дальше и дальше от ключа, в зависимости от количества запросов. Это позволяет популярным поискам быстрее находить хранилище. Поскольку значение возвращается из узлов, которые находятся дальше от ключа, это устраняет возможные «горячие точки». Кэширующие узлы будут сбрасывать значение через определенное время в зависимости от их расстояния от ключа.

Некоторые реализации (например, Kad ) не имеют ни репликации, ни кэширования. Цель этого — быстро удалить старую информацию из системы. Узел, предоставляющий файл, будет периодически обновлять информацию в сети (выполнять сообщения FIND_NODE и STORE). Когда все узлы, имеющие файл, перейдут в автономный режим, никто не будет обновлять его значения (источники и ключевые слова), и информация в конечном итоге исчезнет из сети.

Присоединение к сети

Узел, который хотел бы присоединиться к сети, должен сначала пройти процесс загрузки . На этом этапе присоединяющийся узел должен знать IP-адрес и порт другого узла — узла загрузки (полученного от пользователя или из сохраненного списка), — который уже участвует в сети Kademlia. Если присоединяющийся узел еще не участвовал в сети, он вычисляет случайный номер идентификатора, который в силу того, что является очень большим случайным числом, с большой вероятностью не будет назначен ни одному другому узлу. Он использует этот идентификатор до выхода из сети.

Присоединяющийся узел вставляет узел bootstrap в один из своих k-buckets . Затем присоединяющийся узел выполняет поиск своего собственного ID в узле bootstrap (единственном другом узле, который он знает). «Самопоиск» заполнит k-buckets других узлов новым идентификатором узла и заполнит k-buckets присоединяющегося узла узлами на пути между ним и узлом bootstrap. После этого присоединяющийся узел обновляет все k-buckets, которые находятся дальше, чем k-bucket, в который попадает узел bootstrap. Это обновление — просто поиск случайного ключа, который находится в пределах этого диапазона k-bucket .

Изначально узлы имеют один k-bucket . Когда k-bucket заполняется, его можно разделить. Разделение происходит, если диапазон узлов в k-bucket охватывает собственный идентификатор узла (значения слева и справа в двоичном дереве). Kademlia даже смягчает это правило для одного «ближайшего узла» k-bucket , потому что обычно один единственный bucket будет соответствовать расстоянию, на котором находятся все узлы, которые находятся ближе всего к этому узлу, их может быть больше k , и мы хотим, чтобы он знал их все. Может оказаться, что вблизи узла существует сильно несбалансированное двоичное поддерево. Если k равно 20, и есть 21+ узлов с префиксом «xxx0011.....», а новый узел — «xxx0000 11001 », новый узел может содержать несколько k-bucket для других 21+ узлов. Это необходимо для того, чтобы гарантировать, что сеть знает обо всех узлах в ближайшем регионе.

Ускоренный поиск

Kademlia использует метрику XOR для определения расстояния. Два идентификатора узла или идентификатор узла и ключ подвергаются операции XOR, и результатом является расстояние между ними. Для каждого бита функция XOR возвращает ноль, если два бита равны, и единицу, если два бита различны. Расстояния в метрике XOR удовлетворяют неравенству треугольника : если A, B и C являются вершинами (точками) треугольника, то расстояние от A до B короче (или равно) суммы расстояний от A до C и от C до B.

Метрика XOR позволяет Kademlia расширять таблицы маршрутизации за пределы отдельных битов. Группы битов можно размещать в k-buckets . Группа битов называется префиксом. Для m-bit префикса будет 2 ^m -1 k-buckets . Отсутствующий k-bucket является дальнейшим расширением дерева маршрутизации, которое содержит идентификатор узла. m-bit префикс сокращает максимальное количество поисков с log ₂ n до log _{2 ^m} n . Это максимальные значения, а среднее значение будет намного меньше, что увеличивает вероятность нахождения узла в k-bucket , который разделяет больше битов, чем просто префикс с целевым ключом.

Узлы могут использовать смеси префиксов в своих таблицах маршрутизации, например, сеть Kad , используемая eMule . ^{[ требуется ссылка ]} Сеть Kademlia может быть даже неоднородной в реализациях таблиц маршрутизации, за счет усложнения анализа поисков.

Академическая значимость

Хотя метрика XOR не нужна для понимания Kademlia, она имеет решающее значение при анализе протокола. Арифметика XOR образует абелеву группу, допускающую закрытый анализ. Другие протоколы и алгоритмы DHT требуют моделирования или сложного формального анализа для прогнозирования поведения и корректности сети. Использование групп битов в качестве информации о маршрутизации также упрощает алгоритмы.

Математический анализ алгоритма

Для анализа алгоритма рассмотрим сеть Kademlia узлов с идентификаторами , каждый из которых представляет собой строку длины , состоящую только из единиц и нулей. Ее можно смоделировать как trie-дерево , в котором каждый лист представляет узел, а помеченный путь от корня к листу представляет его идентификатор. Для узла пусть будет набором узлов (идентификаторов), которые разделяют префикс с длины . Тогда заполнение -го ведра из можно смоделировать как добавление указателей из листа в листья (идентификаторы), выбранные равномерно случайным образом из . Таким образом, маршрутизацию можно рассматривать как переход между листьями вдоль этих указателей таким образом, что каждый шаг идет к целевому идентификатору как можно дальше, т. е. жадным образом. ${\displaystyle n}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle d}$ ${\displaystyle x\in \{x_{1},\ldots ,x_{n}\}}$ ${\displaystyle {\mathcal {D}}_{i}(x)}$ ${\displaystyle x}$ ${\displaystyle d-i}$ ${\displaystyle i}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle k}$ ${\displaystyle {\mathcal {D}}_{i}(x)}$

Пусть будет числом прыжков, необходимых для перехода от листа к целевому идентификатору . Предполагая, что выбираются детерминированно из , было доказано, что ${\displaystyle T_{xy}}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \{0,1\}^{d}}$

${\displaystyle \sup _{x_{1},\ldots ,x_{n}}\,\sup _{x\in \{x_{1},\ldots ,x_{n}\}}\,\sup _{y\in \{0,1\}^{d}}\mathbb {E} [T_{xy}]\leq (1+o(1)){\frac {\log n}{H_{k}}},}$

где - -ое гармоническое число . Так как , когда велико, ограничено сверху примерно , однако идентификаторы и цель выбираются. ^[7] Это подтверждает интуицию, что в Kademlia только узлы связываются при поиске целевого узла. ${\displaystyle H_{k}}$ ${\displaystyle k}$ ${\displaystyle H_{k}/\log k\to 1}$ ${\displaystyle k\to \infty }$ ${\displaystyle k}$ ${\displaystyle \mathbb {E} T_{xy}}$ ${\displaystyle \log _{k}n}$ ${\displaystyle O(\log n)}$

Чтобы сделать модель более приближенной к реальным сетям Kademlia, можно также предположить, что выбираются равномерно случайным образом без замены из . Тогда можно доказать, что для всех и , ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \{0,1\}^{d}}$ ${\displaystyle x\in \{x_{1},\ldots ,x_{n}\}}$ ${\displaystyle y\in \{0,1\}^{d}}$

${\displaystyle {\begin{aligned}&T_{xy}{\xrightarrow {p}}{\frac {\log n}{c_{k}}},\\&\mathbb {E} [T_{xy}]\to {\frac {\log n}{c_{k}}},\end{aligned}}}$

где — константа, зависящая только от с как . Таким образом, для больших, сходится к константе, близкой . Это означает, что число узлов, с которыми необходимо связаться при поиске целевого узла, на самом деле в среднем. ^[8] ${\displaystyle c_{k}}$ ${\displaystyle k}$ ${\displaystyle c_{k}/H_{k}\to 1}$ ${\displaystyle k\to \infty }$ ${\displaystyle k}$ ${\displaystyle \mathbb {E} T_{xy}/\log _{k}n}$ ${\displaystyle 1}$ ${\displaystyle \Theta (\log n)}$

Использование в файлообменных сетях

Kademlia используется в файлообменных сетях. Выполняя поиск по ключевым словам Kademlia, можно найти информацию в файлообменной сети, чтобы ее можно было загрузить. Поскольку нет центрального экземпляра для хранения индекса существующих файлов, эта задача делится поровну между всеми клиентами: если узел хочет поделиться файлом, он обрабатывает содержимое файла, вычисляя из него число ( хэш ), которое будет идентифицировать этот файл в файлообменной сети. Поскольку хэши файлов и идентификаторы узлов имеют одинаковую длину, клиент может использовать функцию расстояния XOR для поиска нескольких узлов, идентификаторы которых близки к хешу, и поручает этим узлам хранить IP-адрес издателя способом, определяемым реализацией. Узлы с идентификаторами, наиболее близкими к хешу файла, будут, таким образом, иметь список IP-адресов пиров/издателей этого файла, с которых клиент может способом, определяемым реализацией, загрузить файл.

Клиенты, желающие загрузить файл с этого издателя, не должны знать IP-адрес издателя (издателей может быть много), а только хэш файла. Ищущий клиент будет использовать Kademlia для поиска в сети узла, идентификатор которого имеет наименьшее расстояние до хэша файла, затем извлечет список источников, который хранится в этом узле.

Поскольку ключ может соответствовать многим значениям, например, многим источникам одного и того же файла, каждый узел хранения может иметь различную информацию. Затем источники запрашиваются из всех k узлов, близких к ключу, где k — размер ведра.

Хэш файла обычно получается из специально сформированной магнитной ссылки в Интернете, найденной в другом месте, или включается в индексный файл, полученный из других источников.

Поиск имени файла реализуется с использованием ключевых слов . Имя файла делится на составляющие его слова. Каждое из этих ключевых слов хэшируется и сохраняется в сети вместе с соответствующим именем файла и хешем файла. Поиск включает выбор одного из ключевых слов, обращение к узлу с идентификатором, наиболее близким к этому хешу ключевого слова, и получение списка имен файлов, содержащих ключевое слово. Поскольку каждое имя файла в списке имеет прикрепленный хэш, выбранный файл затем может быть получен обычным способом.

Реализации

Сети

Публичные сети, использующие алгоритм Kademlia (эти сети несовместимы друг с другом):

• I2P : анонимный оверлейный сетевой уровень. ^[9]
• Сеть Kad : изначально разработана сообществом eMule для замены серверной архитектуры сети eDonkey .
• Ethereum : протокол обнаружения узлов в сетевом стеке блокчейна Ethereum основан на слегка измененной реализации Kademlia. ^[10]
• Overnet : С KadC доступна библиотека C для работы с Kademlia. (разработка Overnet прекращена)
• Основной DHT : DHT для BitTorrent , основанный на реализации алгоритма Kademlia, для торрентов без трекеров.
• Osiris (все версии): используется для управления распределенным и анонимным веб-порталом.
• Retroshare : децентрализованная платформа общения F2F с защищенной голосовой связью по IP-протоколу, мгновенным обменом сообщениями, передачей файлов и т. д.
• Tox : полностью распределенная платформа обмена сообщениями, VoIP и видеочата
• Gnutella DHT: изначально разработан LimeWire ^{[11] [12]} для расширения протокола Gnutella с целью поиска альтернативных местоположений файлов, теперь используется другими клиентами Gnutella. ^[13]
• IPFS : одноранговая распределенная файловая система на основе libp2p. ^[14]
• TeleHash : протокол ячеистой сети, который использует Kademlia для разрешения прямых соединений между сторонами. ^[15]
• iMule: служебное программное обеспечение для обмена файлами для I2P .
• OpenDHT: библиотека, обеспечивающая реализацию Kademlia, используемая Джами и другими. ^[16]
• GNUnet : альтернативный сетевой стек для создания безопасных, децентрализованных и сохраняющих конфиденциальность распределенных приложений. Использует рандомизированную версию Kademlia под названием R5N. ^[17]
• Dat : одноранговый инструмент обмена файлами, основанный на ^{[ требуется ссылка ] [ требуется пояснение ]} на протоколе Hypercore. ^[18]

Смотрите также

• Контентно-адресуемая сеть
• Аккорд (одноранговый)
• Гобелен (DHT)
• Выпечка (DHT)
• Коорде

Ссылки

1. Maymounkov, Petar; Mazieres, David. "Kademlia: одноранговая информационная система на основе метрики XOR" (PDF) . pdos.csail.mit.edu . Получено 28.12.2023 .
2. "Документы Дэвида Мазьера". www.scs.stanford.edu .
3. "Сетевая база данных - I2P". geti2p.net .
4. Maymounkov, Petar; Mazieres, David. "Kademlia: A Peer-to-Peer Information System Based on the XOR Metric" (PDF) . Stanford Secure Computer Systems Group . Получено 28.12.2023 .
5. Стефан Сароиу, П. Кришна Гуммади и Стивен Д. Гриббл. Исследование измерений одноранговых систем обмена файлами. Технический отчет UW-CSE-01-06-02, Вашингтонский университет, кафедра компьютерных наук и техники, июль 2001 г.
6. Дэниел Штутцбах и Реза Реджайе. Понимание оттока в одноранговых сетях, раздел 5.5. Предсказуемость времени безотказной работы, Конференция по измерению Интернета, Рио-де-Жанейро, октябрь 2006 г.
7. Cai, XS; Devroye, L. (2013). «Вероятностный анализ сетей Kademlia». Алгоритмы и вычисления . Конспект лекций по информатике. Том 8283. С. 711–721. arXiv : 1309.5866 . doi :10.1007/978-3-642-45030-3_66. ISBN 978-3-642-45029-7. S2CID  6068991.
8. Cai, Xing Shi; Devroye, Luc (2015). «Анализ Kademlia для случайных идентификаторов». Internet Mathematics . 11 (6): 1–16. arXiv : 1402.1191 . doi : 10.1080/15427951.2015.1051674. ISSN  1542-7951. S2CID  16547375.
9. "Введение - I2P". geti2p.net .
10. "GitHub - ethereum/wiki: The Ethereum Wiki". 25 марта 2019 г. – через GitHub.
11. "Slyck News - LimeWire вернул себе первую позицию Download.com". www.slyck.com . Архивировано из оригинала 2019-01-19 . Получено 2007-06-20 .
12. "Mojito - LimeWire". wiki.limewire.org . Архивировано из оригинала 17 февраля 2009 года.
13. "Gtk-gnutella changelog". sourceforge.net . Архивировано из оригинала 23 июля 2011 . Получено 23 января 2010 .
14. "Документ IPFS" (PDF) . GitHub .
15. "#7: Джереми Миллер - TeleHash" . Получено 2016-03-12 .
16. «Дом». OpenDHT Wiki. Гитхаб . Ноу-хау Linux . Проверено 19 марта 2021 г.
17. «R5N: Рандомизированная рекурсивная маршрутизация для сетей с ограниченной маршрутизацией» (PDF) .
18. "Hypercore Protocol". Архивировано из оригинала 2020-12-23 . Получено 2020-12-27 .

Внешние ссылки

• Xlattice проекты Kademlia Спецификации и определения.