Вибрация струны

Волна

Вибрация, стоячие волны в струне. Основной тон и первые 5 обертонов в гармоническом ряду .

Вибрация струны — это волна . Резонанс заставляет вибрирующую струну издавать звук с постоянной частотой , т. е. постоянной высотой тона . Если длина или натяжение струны отрегулированы правильно, то издаваемый звук представляет собой музыкальный тон . Вибрирующие струны являются основой струнных инструментов, таких как гитары , виолончели и фортепиано .

Волна

Скорость распространения волны в струне ( ) пропорциональна квадратному корню из силы натяжения струны ( ) и обратно пропорциональна квадратному корню из линейной плотности ( ) струны: ${\displaystyle v}$ ${\displaystyle T}$ ${\displaystyle \mu }$

${\displaystyle v={\sqrt {T \over \mu }}.}$

Эту связь открыл Винченцо Галилей в конце 1500-х годов. ^{[ необходима цитата ]}

Вывод

Иллюстрация вибрирующей струны

Источник: ^[1]

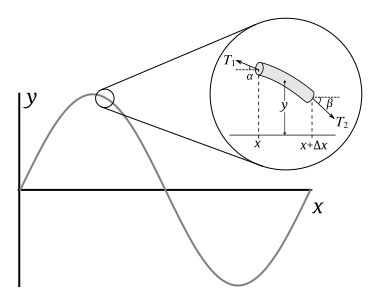
Пусть будет длиной куска струны, его массой и его линейной плотностью . Если углы и малы, то горизонтальные компоненты натяжения с обеих сторон могут быть аппроксимированы константой , для которой чистая горизонтальная сила равна нулю. Соответственно, используя приближение малого угла, горизонтальные натяжения, действующие с обеих сторон сегмента струны, определяются как ${\displaystyle \Delta x}$ ${\displaystyle m}$ ${\displaystyle \mu }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle T}$

${\displaystyle T_{1x}=T_{1}\cos(\alpha )\approx T.}$

${\displaystyle T_{2x}=T_{2}\cos(\beta )\approx T.}$

Из второго закона Ньютона для вертикальной составляющей следует, что масса (которая является произведением ее линейной плотности и длины) этого куска, умноженного на его ускорение, будет равна результирующей силе, действующей на этот кусок: ${\displaystyle a}$

${\displaystyle \Sigma F_{y}=T_{1y}-T_{2y}=-T_{2}\sin(\beta )+T_{1}\sin(\alpha )=\Delta ma\approx \mu \Delta x{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Разделив это выражение на и подставив первое и второе уравнения, получаем (мы можем выбрать либо первое, либо второе уравнение для , поэтому нам удобно выбрать каждое из них с соответствующим углом и ) ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle \beta }$ ${\displaystyle \alpha }$

${\displaystyle -{\frac {T_{2}\sin(\beta )}{T_{2}\cos(\beta )}}+{\frac {T_{1}\sin(\alpha )}{T_{1}\cos(\alpha )}}=-\tan(\beta )+\tan(\alpha )={\frac {\mu \Delta x}{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Согласно приближению малых углов, тангенсы углов на концах отрезка струны равны наклонам на концах с дополнительным знаком минус из-за определения и . Использование этого факта и перестановка дает ${\displaystyle \alpha }$ ${\displaystyle \beta }$

${\displaystyle {\frac {1}{\Delta x}}\left(\left.{\frac {\partial y}{\partial x}}\right|^{x+\Delta x}-\left.{\frac {\partial y}{\partial x}}\right|^{x}\right)={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

В пределе, стремящемся к нулю, левая часть представляет собой определение второй производной от : ${\displaystyle \Delta x}$ ${\displaystyle y}$

${\displaystyle {\frac {\partial ^{2}y}{\partial x^{2}}}={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Это волновое уравнение для , а коэффициент при второй производной по времени равен ; таким образом ${\displaystyle y(x,t)}$ ${\displaystyle {\frac {1}{v^{2}}}}$

${\displaystyle v={\sqrt {T \over \mu }},}$

Где — скорость распространения волны в струне ( подробнее об этом см. в статье о волновом уравнении ). Однако этот вывод действителен только для колебаний малой амплитуды; для колебаний большой амплитуды — не является хорошим приближением для длины куска струны, горизонтальная составляющая натяжения не обязательно постоянна. Горизонтальные натяжения плохо аппроксимируются . ${\displaystyle v}$ ${\displaystyle \Delta x}$ ${\displaystyle T}$

Частота волны

Зная скорость распространения, можно вычислить частоту звука, производимого струной. Скорость распространения волны равна длине волны, деленной на период , или умноженной на частоту : ${\displaystyle \lambda }$ ${\displaystyle \tau }$ ${\displaystyle f}$

${\displaystyle v={\frac {\lambda }{\tau }}=\lambda f.}$

Если длина струны равна , то основная гармоника — это та, которая создается вибрацией, узлами которой являются два конца струны, то есть половина длины волны основной гармоники. Отсюда получаем законы Мерсенна : ${\displaystyle L}$ ${\displaystyle L}$

${\displaystyle f={\frac {v}{2L}}={1 \over 2L}{\sqrt {T \over \mu }}}$

где - натяжение (в Ньютонах), - линейная плотность (то есть масса на единицу длины), - длина колеблющейся части струны. Следовательно: ${\displaystyle T}$ ${\displaystyle \mu }$ ${\displaystyle L}$

• чем короче струна, тем выше частота основного тона
• чем выше напряжение, тем выше частота основного тона
• чем легче струна, тем выше частота основного тона

Более того, если мы возьмем n-ю гармонику, имеющую длину волны, заданную выражением , то мы легко получим выражение для частоты n-й гармоники: ${\displaystyle \lambda _{n}=2L/n}$

${\displaystyle f_{n}={\frac {nv}{2L}}}$

А для струны под действием натяжения T с линейной плотностью , то ${\displaystyle \mu }$

${\displaystyle f_{n}={\frac {n}{2L}}{\sqrt {\frac {T}{\mu }}}}$

Наблюдение за колебаниями струны

Можно увидеть формы волн на вибрирующей струне, если частота достаточно низкая, и вибрирующая струна удерживается перед экраном ЭЛТ, например, экрана телевизора или компьютера ( не аналогового осциллографа). Этот эффект называется стробоскопическим эффектом , а скорость, с которой струна, по-видимому, вибрирует, является разницей между частотой струны и частотой обновления экрана. То же самое может произойти с люминесцентной лампой , со скоростью, которая является разницей между частотой струны и частотой переменного тока . (Если частота обновления экрана равна частоте струны или кратна ей, струна будет казаться неподвижной, но деформированной.) При дневном свете и других неколеблющихся источниках света этот эффект не возникает, и струна кажется неподвижной, но более толстой, и более светлой или размытой из-за инерционности зрения .

Похожий, но более контролируемый эффект можно получить с помощью стробоскопа . Это устройство позволяет согласовывать частоту ксеноновой лампы с частотой вибрации струны. В темной комнате это четко показывает форму волны. В противном случае можно использовать изгиб или, что, возможно, проще, регулировку головок машины, чтобы получить ту же или кратную частоту переменного тока для достижения того же эффекта. Например, в случае гитары, 6-я (самая низкая) струна, прижатая к третьему ладу, дает G на частоте 97,999 Гц. Небольшая регулировка может изменить ее до 100 Гц, ровно на одну октаву выше частоты переменного тока в Европе и большинстве стран Африки и Азии, 50 Гц. В большинстве стран Америки, где частота переменного тока составляет 60 Гц, изменение A# на пятой струне, на первом ладу, со 116,54 Гц до 120 Гц дает аналогичный эффект.

Смотрите также

• Инструменты с ладами
• Музыкальная акустика
• Вибрации круглого барабана
• Эксперимент Мельде
• 3-й мост (гармонический резонанс, основанный на равном разделении струн)
• Резонанс струн
• Изменение фазы отражения

Ссылки

• Molteno, TCA; NB Tufillaro (сентябрь 2004 г.). «Экспериментальное исследование динамики струны». American Journal of Physics . 72 (9): 1157–1169. Bibcode : 2004AmJPh..72.1157M. doi : 10.1119/1.1764557.
• Туфилларо, Н. Б. (1989). «Нелинейные и хаотические колебания струн». Американский журнал физики . 57 (5): 408. Bibcode : 1989AmJPh..57..408T. doi : 10.1119/1.16011.

Специфический

1. Волновое уравнение и скорость волны

Внешние ссылки

• «Вибрирующая струна» Алена Горели и Марка Робертсона-Тесси, проект «Демонстрации Вольфрама» .