
Алгебраическая теория графов — раздел математики , в котором алгебраические методы применяются к задачам о графах . В этом отличие от геометрического , комбинаторного или алгоритмического подходов. Есть три основных раздела алгебраической теории графов, включающие использование линейной алгебры , использование теории групп и изучение инвариантов графов .
Первая ветвь алгебраической теории графов включает изучение графов в связи с линейной алгеброй . В частности, он изучает спектр матрицы смежности или матрицы Лапласа графа (эта часть алгебраической теории графов также называется спектральной теорией графов ). Например, для графа Петерсена спектр матрицы смежности равен (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Несколько теорем связывают свойства спектра с другими свойствами графа . В качестве простого примера: связный граф диаметром D будет иметь в своем спектре не менее D +1 различных значений. [ 1] Аспекты спектров графов использовались при анализе синхронизируемости сетей .
Вторая ветвь алгебраической теории графов включает изучение графов в связи с теорией групп , особенно группами автоморфизмов и геометрической теорией групп . Основное внимание уделяется различным семействам графов, основанным на симметрии (таким как симметричные графы , вершинно-транзитивные графы , реберно-транзитивные графы , дистанционно-транзитивные графы , дистанционно-регулярные графы и сильно регулярные графы ), а также отношениям включения между эти семьи. Некоторые из таких категорий графов настолько редки, что можно составлять списки графов. По теореме Фрухта все группы можно представить как группу автоморфизмов связного графа (действительно, кубического графа ). [2] Другая связь с теорией групп заключается в том, что для любой группы могут быть созданы симметричные графы, известные как графы Кэли , и они обладают свойствами, связанными со структурой группы. [1]

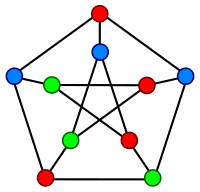
Эта вторая ветвь алгебраической теории графов связана с первой, поскольку свойства симметрии графа отражаются в его спектре. В частности, спектр высокосимметричного графа, такого как граф Петерсена, имеет мало различных значений [1] (у графа Петерсена их 3, что является минимально возможным, учитывая его диаметр). Для графов Кэли спектр может быть напрямую связан со структурой группы, в частности с ее неприводимыми характерами . [1] [3]
Наконец, третья ветвь алгебраической теории графов касается алгебраических свойств инвариантов графов, и особенно хроматического полинома , полинома Тутта и инвариантов узлов . Например, хроматический полином графа подсчитывает количество собственных раскрасок вершин . Для графа Петерсена этот полином равен . [1] В частности, это означает, что граф Петерсена не может быть правильно раскрашен в один или два цвета, но может быть раскрашен 120 различными способами с помощью 3 цветов. Большая часть работ в этой области алгебраической теории графов была мотивирована попытками доказать теорему о четырёх цветах . Однако остается еще много открытых проблем , таких как определение характеристик графов, имеющих одинаковый хроматический полином, и определение того, какие полиномы являются хроматическими.