Альфа-бета-отсечение — это алгоритм поиска , который стремится уменьшить количество узлов, которые оцениваются алгоритмом минимакса в его дереве поиска . Это состязательный алгоритм поиска, обычно используемый для машинной игры в комбинаторные игры для двух игроков ( крестики-нолики , шахматы , Connect 4 и т. д.). Он прекращает оценку хода, когда найдена хотя бы одна возможность, которая доказывает, что ход хуже, чем ранее рассмотренный ход. Такие ходы не нужно оценивать дальше. При применении к стандартному дереву минимакса он возвращает тот же ход, что и минимакс, но отсекает ветви, которые не могут повлиять на окончательное решение. [1]
Джон Маккарти во время Dartmouth Workshop встретил Алекса Бернстайна из IBM , который писал шахматную программу. Маккарти изобрел альфа-бета-поиск и рекомендовал его ему, но Бернстайна это «не убедило». [2]
Аллен Ньюэлл и Герберт А. Саймон , которые использовали то, что Джон Маккарти называет «приближением» [3] в 1958 году, написали, что альфа-бета «похоже, была изобретена заново несколько раз». [4] Артур Сэмюэл имел раннюю версию для моделирования шашек. Ричардс, Тимоти Харт, Майкл Левин и/или Дэниел Эдвардс также изобрели альфа-бета независимо в Соединенных Штатах . [5] Маккарти предложил похожие идеи во время семинара в Дартмуте в 1956 году и предложил их группе своих студентов, включая Алана Котока в Массачусетском технологическом институте в 1961 году. [6] Александр Брудно независимо придумал алгоритм альфа-бета, опубликовав свои результаты в 1963 году. [7] Дональд Кнут и Рональд В. Мур усовершенствовали алгоритм в 1975 году. [8] [9] Джуда Перл доказал его оптимальность с точки зрения ожидаемого времени выполнения для деревьев со случайно назначенными значениями листьев в двух статьях. [10] [11] Оптимальность рандомизированной версии альфа-бета была показана Майклом Саксом и Ави Вигдерсоном в 1986 году. [12]
Дерево игры может представлять множество игр с нулевой суммой для двух игроков , таких как шахматы, шашки и реверси. Каждый узел в дереве представляет возможную ситуацию в игре. Каждому конечному узлу (исходу) ветви присваивается числовой счет, который определяет ценность результата для игрока при следующем ходе. [13]
Алгоритм поддерживает два значения, альфа и бета, которые соответственно представляют минимальный счет, который гарантирован максимизирующему игроку, и максимальный счет, который гарантирован минимизирующему игроку. Изначально альфа — это отрицательная бесконечность, а бета — это положительная бесконечность, т. е. оба игрока начинают с наихудшего возможного счета. Всякий раз, когда максимальный счет, который гарантирован минимизирующему игроку (т. е. игроку «бета»), становится меньше минимального счета, который гарантирован максимизирующему игроку (т. е. игроку «альфа») (т. е. бета < альфа), игроку «максимизирующему» не нужно рассматривать дальнейших потомков этого узла, поскольку они никогда не будут достигнуты в фактической игре.
Чтобы проиллюстрировать это на примере из реальной жизни, предположим, что кто-то играет в шахматы, и настала его очередь. Ход «A» улучшит позицию игрока. Игрок продолжает искать ходы, чтобы убедиться, что лучший не был упущен. Ход «B» также является хорошим ходом, но затем игрок понимает, что он позволит противнику форсировать мат в два хода. Таким образом, другие результаты от хода B больше не нужно рассматривать, поскольку противник может форсировать победу. Максимальный счет, который противник может форсировать после хода «B», равен отрицательной бесконечности: проигрыш для игрока. Это меньше минимальной позиции, которая была найдена ранее; ход «A» не приводит к вынужденному проигрышу в два хода.

Преимущество альфа-бета-отсечения заключается в том, что ветви дерева поиска могут быть устранены. [13] Таким образом, время поиска может быть ограничено «более перспективным» поддеревом, и более глубокий поиск может быть выполнен за то же время. Как и его предшественник, он относится к классу алгоритмов ветвей и границ . Оптимизация уменьшает эффективную глубину до чуть более половины от простого минимакса, если узлы оцениваются в оптимальном или близком к оптимальному порядке (лучший выбор для стороны при движении, упорядоченной первой в каждом узле).
При (среднем или постоянном) факторе ветвления b и глубине поиска d plies максимальное количество оцениваемых позиций листовых узлов (когда порядок ходов пессимистичен) составляет O ( b d ) — то же самое, что и при простом минимаксном поиске. Если порядок ходов для поиска оптимален (то есть лучшие ходы всегда ищутся первыми), количество оцениваемых позиций листовых узлов составляет около O ( b ×1× b ×1×...× b ) для нечетной глубины и O ( b ×1× b ×1×...×1) для четной глубины, или . В последнем случае, когда ply поиска четный, эффективный фактор ветвления уменьшается до его квадратного корня , или, что эквивалентно, поиск может быть в два раза глубже при том же количестве вычислений. [14] Объяснение b ×1× b ×1×... заключается в том, что все ходы первого игрока должны быть изучены, чтобы найти лучший, но для каждого из них требуется только лучший ход второго игрока, чтобы опровергнуть все, кроме первого (и лучшего) хода первого игрока — альфа-бета гарантирует, что никакие другие ходы второго игрока не нужно рассматривать. Когда узлы рассматриваются в случайном порядке (т. е. алгоритм рандомизирует), асимптотически ожидаемое количество узлов, оцененных в однородных деревьях с бинарными значениями листьев, равно . [12] Для тех же деревьев, когда значения назначаются значениям листьев независимо друг от друга и, скажем, ноль и единица оба равновероятны, ожидаемое количество оцененных узлов равно , что намного меньше работы, проделанной рандомизированным алгоритмом, упомянутым выше, и снова является оптимальным для таких случайных деревьев. [10] Когда значения листьев выбираются независимо друг от друга, но из интервала равномерно случайным образом, ожидаемое количество оцененных узлов увеличивается до в пределе, [11] что снова является оптимальным для этого вида случайного дерева. Обратите внимание, что фактическая работа для «малых» значений лучше аппроксимируется с помощью . [11] [10]
Шахматная программа, которая ищет четыре хода со средним числом 36 ветвей на узел, оценивает более миллиона конечных узлов. Оптимальное сокращение альфа-бета устранит все, кроме около 2000 конечных узлов, сокращение на 99,8%. [13]
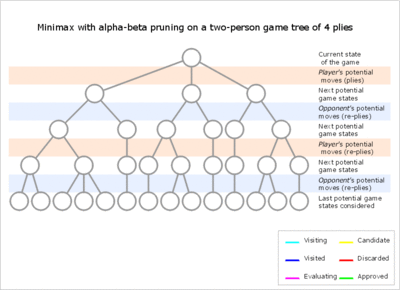
Обычно во время альфа-бета поддеревья временно доминируют либо за счет преимущества первого игрока (когда многие ходы первого игрока хороши, и на каждой глубине поиска первый ход, проверенный первым игроком, является адекватным, но все ответы второго игрока требуются для попытки найти опровержение), либо наоборот. Это преимущество может переходить на другую сторону много раз во время поиска, если порядок ходов неверен, что каждый раз приводит к неэффективности. Поскольку количество искомых позиций уменьшается экспоненциально с каждым ходом ближе к текущей позиции, стоит потратить значительные усилия на сортировку ранних ходов. Улучшенная сортировка на любой глубине экспоненциально сократит общее количество искомых позиций, но сортировка всех позиций на глубинах вблизи корневого узла относительно дешева, поскольку их так мало. На практике порядок ходов часто определяется результатами более ранних, меньших поисков, например, посредством итеративного углубления .
Кроме того, этот алгоритм может быть тривиально модифицирован для возврата целой принципиальной вариации в дополнение к оценке. Некоторые более агрессивные алгоритмы, такие как MTD(f), не позволяют легко осуществить такую модификацию.
Псевдокод для минимакса с ограниченной глубиной и альфа-бета-отсечением выглядит следующим образом: [15]
Реализации отсечения альфа-бета часто можно очертить по тому, являются ли они «fail-soft» или «fail-hard». При fail-soft alpha-beta функция alphabeta может возвращать значения (v), которые превышают (v < α или v > β) границы α и β, установленные аргументами вызова функции. Для сравнения, fail-hard alpha-beta ограничивает возвращаемое значение своей функции включительным диапазоном α и β. Основное различие между fail-soft и fail-hard реализациями заключается в том, обновляются ли α и β до или после проверки отсечения. Если они обновляются до проверки, то они могут превышать начальные границы, и алгоритм является fail-soft.
Следующий псевдокод иллюстрирует отказоустойчивый вариант. [15]
Функция alphabeta(node, depth, α, β, maximizingPlayer) возвращает эвристическое значение узла , если depth == 0 или node является конечным. Если maximizingPlayer , то значение := −∞ для каждого потомка узла сделать значение := max(значение, алфавитa(дочерний элемент, глубина − 1, α, β, ЛОЖЬ)) если значение > β , то перерыв (* β отсечка *) α := max(α, значение) возвращаемое значение в противном случае значение := +∞ для каждого потомка узла сделать значение := min(значение, алфавитa(ребенок, глубина − 1, α, β, ИСТИНА)) если значение < α , то перерыв (* α отсечка *) β := min(β, значение) возвращаемое значение
(* Начальный вызов *) alphabeta(origin, depth, − ∞ , + ∞ , TRUE)
Следующий псевдокод иллюстрирует отказоустойчивую альфа-бета.
Функция alphabeta(node, depth, α, β, maximizingPlayer) возвращает эвристическое значение узла , если depth == 0 или node является конечным. Если maximizingPlayer , то значение := −∞ для каждого потомка узла сделать значение := max(значение, алфавитa(дочерний элемент, глубина − 1, α, β, ЛОЖЬ)) α := max(α, значение) если значение ≥ β , то прерываем (* β cutoff *) возвращаем значение , иначе значение := +∞ для каждого потомка узла сделать значение := min(значение, алфавитa(ребенок, глубина − 1, α, β, ИСТИНА)) β := min(β, значение) если значение ≤ α , то прерывание (* α cutoff *) возврат значения
(* Начальный вызов *) alphabeta(origin, depth, − ∞ , + ∞ , TRUE)
Дальнейшее улучшение может быть достигнуто без ущерба для точности путем использования упорядочивающих эвристик для поиска более ранних частей дерева, которые, вероятно, приведут к альфа-бета-отсечениям. Например, в шахматах ходы, которые захватывают фигуры, могут быть рассмотрены до ходов, которые этого не делают, а ходы, которые получили высокие баллы в более ранних проходах через анализ дерева игры, могут быть оценены до других. Другой распространенной и очень дешевой эвристикой является эвристика-убийца , где последний ход, который вызвал бета-отсечение на том же уровне дерева в поиске дерева, всегда рассматривается первым. Эту идею также можно обобщить в набор таблиц опровержений .
Поиск альфа-бета можно сделать еще быстрее, если рассматривать только узкое окно поиска (обычно определяемое догадками на основе опыта). Это известно как окно стремления . В крайнем случае поиск выполняется с равными альфа и бета; метод, известный как поиск с нулевым окном , поиск с нулевым окном или поиск разведчика . Это особенно полезно для поисков выигрышей/проигрышей ближе к концу игры, где дополнительная глубина, полученная от узкого окна и простой функции оценки выигрышей/проигрышей, может привести к окончательному результату. Если поиск стремления не удается, легко определить, был ли он неудачным высоко (верхний край окна был слишком низким) или низко (нижний край окна был слишком высоким). Это дает информацию о том, какие значения окна могут быть полезны при повторном поиске позиции.
Со временем были предложены другие улучшения, и действительно, идея Falphabeta (fail-soft alpha–beta) Джона Фишберна почти универсальна и уже включена выше в слегка измененной форме. Фишберн также предложил комбинацию эвристики killer и поиска с нулевым окном под названием Lalphabeta («последний ход с минимальным окном поиска alpha–beta»).
Поскольку алгоритм минимакса и его варианты изначально являются алгоритмами поиска в глубину , такая стратегия, как итеративное углубление , обычно используется в сочетании с альфа-бета, чтобы можно было вернуть достаточно хороший ход, даже если алгоритм прерывается до того, как он закончил выполнение. Еще одним преимуществом использования итеративного углубления является то, что поиск на более мелких глубинах дает подсказки о порядке ходов, а также неглубокие оценки альфа и бета, которые могут помочь создать отсечки для поиска на более высокой глубине гораздо раньше, чем это было бы возможно в противном случае.
С другой стороны, такие алгоритмы, как SSS* , используют стратегию best-first . Это может потенциально сделать их более эффективными по времени, но обычно за счет высокой эффективности пространства. [16]
Как и его аналог A* для однопользовательских игр, SSS* оптимален с точки зрения среднего числа проверенных узлов; но его превосходная способность к отсечению более чем компенсируется значительным объемом дискового пространства и необходимыми требованиями к учету.