Проверка честности монеты

В статистике вопрос проверки честности монеты — это вопрос, важность которого заключается, во-первых, в предоставлении простой задачи, на которой можно проиллюстрировать основные идеи статистического вывода , и, во-вторых, в предоставлении простой задачи, которую можно использовать для сравнения различных конкурирующих методов статистического вывода, включая теорию принятия решений . Практическая задача проверки честности монеты может считаться легко решаемой путем проведения достаточно большого количества испытаний, но статистика и теория вероятностей могут дать рекомендации по двум типам вопросов; в частности, по вопросам о том, сколько испытаний следует провести, и по вопросам точности оценки вероятности выпадения орла, полученной из заданной выборки испытаний.

Честная монета — это идеализированное рандомизирующее устройство с двумя состояниями (обычно называемыми «орел» и «решка» ), которые могут возникнуть с равной вероятностью. Оно основано на подбрасывании монеты, широко используемом в спорте и других ситуациях, где требуется дать двум сторонам одинаковые шансы на победу. Используется либо специально разработанный чип , либо, что более типично, простая денежная монета , хотя последняя может быть немного «несправедливой» из-за асимметричного распределения веса, что может привести к тому, что одно состояние будет происходить чаще, чем другое, давая одной из сторон несправедливое преимущество. ^[1] Поэтому может потребоваться экспериментальная проверка того, является ли монета на самом деле «честной» — то есть, составляет ли вероятность того, что монета упадет на любую сторону при подбрасывании, ровно 50%. Конечно, невозможно исключить произвольно малые отклонения от справедливости, такие, которые, как можно ожидать, повлияют только на одно подбрасывание за всю жизнь подбрасываний; также всегда возможно, что нечестная (или « предвзятая ») монета выпадет ровно 10 орлов за 20 подбрасываний. Поэтому любой тест на справедливость должен устанавливать только определенную степень уверенности в определенной степени справедливости (определенное максимальное смещение). В более строгой терминологии проблема заключается в определении параметров процесса Бернулли , учитывая только ограниченную выборку испытаний Бернулли .

Преамбула

В этой статье описываются экспериментальные процедуры определения честности или нечестности монеты. Существует множество статистических методов анализа такой экспериментальной процедуры. В этой статье проиллюстрированы два из них.

Оба метода предполагают эксперимент (или испытание), в котором монета подбрасывается много раз, и результат каждого подбрасывания записывается. Затем результаты можно проанализировать статистически, чтобы решить, является ли монета «честной» или «вероятно нечестной».

• Функция плотности апостериорной вероятности , или PDF ( байесовский подход ). Изначально истинная вероятность получения определенной стороны при подбрасывании монеты неизвестна, но неопределенность представлена ​​« априорным распределением ». Теория байесовского вывода используется для вывода апостериорного распределения путем объединения априорного распределения и функции правдоподобия , которая представляет собой информацию, полученную в ходе эксперимента. Вероятность того, что данная монета является «честной монетой», затем может быть получена путем интегрирования PDF апостериорного распределения по соответствующему интервалу, который представляет все вероятности, которые можно считать «честными» в практическом смысле.
• Оценка истинной вероятности ( частотный подход ). Этот метод предполагает, что экспериментатор может решить подбросить монету любое количество раз. Экспериментатор сначала определяет требуемый уровень уверенности и допустимую погрешность. Эти параметры определяют минимальное количество подбрасываний, которые необходимо выполнить для завершения эксперимента.

Важное различие между этими двумя подходами заключается в том, что первый подход придает некоторый вес предыдущему опыту подбрасывания монет, а второй — нет. Вопрос о том, какой вес придавать предыдущему опыту в зависимости от качества (достоверности) этого опыта, обсуждается в рамках теории достоверности .

Апостериорная функция плотности вероятности

Одним из методов является расчет апостериорной функции плотности вероятности байесовской теории вероятностей .

Тест проводится путем подбрасывания монеты N раз и регистрации наблюдаемых чисел орла, h и решки, t . Символы H и T представляют собой более обобщенные переменные, выражающие число орлов и решек соответственно, которые могли бы наблюдаться в эксперименте. Таким образом, N = H + T = h + t .

Далее, пусть r будет фактической вероятностью получения орла при одном подбрасывании монеты. Это свойство монеты, которое исследуется. Используя теорему Байеса , апостериорная плотность вероятности r, условная на h и t, выражается следующим образом:

${\displaystyle f(r\mid H=h,T=t)={\frac {\Pr(H=h\mid r,N=h+t)\,g(r)}{\int _{0}^{1}\Pr(H=h\mid p,N=h+t)\,g(p)\,dp}},}$

где g ( r ) представляет собой априорное распределение плотности вероятности r , которое лежит в диапазоне от 0 до 1.

Априорное распределение плотности вероятности суммирует то, что известно о распределении r при отсутствии какого-либо наблюдения. Мы предположим, что априорное распределение r равномерно на интервале [0, 1]. То есть g ( r ) = 1. (На практике было бы более уместно предположить априорное распределение, которое имеет гораздо больший вес в области около 0,5, чтобы отразить наш опыт с реальными монетами .)

Вероятность выпадения h орлов при N подбрасываниях монеты с вероятностью выпадения орла, равной r, определяется биномиальным распределением :

${\displaystyle \Pr(H=h\mid r,N=h+t)={N \choose h}r^{h}(1-r)^{t}.}$

Подставим это в предыдущую формулу:

${\displaystyle f(r\mid H=h,T=t)={\frac {{N \choose h}r^{h}(1-r)^{t}}{\int _{0}^{1}{N \choose h}p^{h}(1-p)^{t}\,dp}}={\frac {r^{h}(1-r)^{t}}{\int _{0}^{1}p^{h}(1-p)^{t}\,dp}}.}$

Фактически это бета-распределение ( сопряженное априорное распределение для биномиального распределения), знаменатель которого можно выразить через бета-функцию :

${\displaystyle f(r\mid H=h,T=t)={\frac {1}{\mathrm {B} (h+1,t+1)}}r^{h}(1-r)^{t}.}$

Поскольку предполагается равномерное априорное распределение, а h и t являются целыми числами, это также можно записать в терминах факториалов :

${\displaystyle f(r\mid H=h,T=t)={\frac {(h+t+1)!}{h!\,t!}}r^{h}(1-r)^{t}.}$

Пример

Например, пусть N = 10, h = 7, т.е. монета подбрасывается 10 раз и получается 7 орлов:

${\displaystyle f(r\mid H=7,T=3)={\frac {(10+1)!}{7!\,3!}}r^{7}(1-r)^{3}=1320\,r^{7}(1-r)^{3}.}$

График справа показывает функцию плотности вероятности r при условии, что за 10 подбрасываний выпало 7 орлов. (Примечание: r — вероятность выпадения орла при однократном подбрасывании одной и той же монеты.)

График плотности вероятности f ( r  |  H  = 7,  T  = 3) = 1320  r ⁷  (1 −  r ) ³ с r в диапазоне от 0 до 1

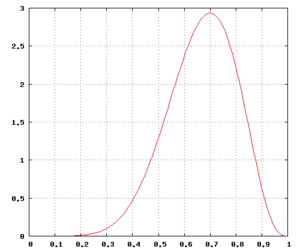
Вероятность для беспристрастной монеты (определяемой для этой цели как монета, вероятность выпадения орла которой составляет от 45% до 55%)

${\displaystyle \Pr(0.45<r<0.55)=\int _{0.45}^{0.55}f(p\mid H=7,T=3)\,dp\approx 13\%\!}$

(незначительно по сравнению с альтернативной гипотезой (смещенная монета). Однако оно недостаточно мало, чтобы заставить нас поверить, что монета имеет значительное смещение. Эта вероятность немного выше, чем наше предположение о вероятности того, что монета была честной, соответствующей равномерному априорному распределению, которое составляло 10%. При использовании априорного распределения, которое отражает наши априорные знания о том, что такое монета и как она действует, апостериорное распределение не будет благоприятствовать гипотезе смещения. Однако количество испытаний в этом примере (10 подбрасываний) очень мало, и при большем количестве испытаний выбор априорного распределения будет несколько менее значимым.)

При равномерном априорном распределении апостериорное распределение вероятностей f ( r  |  H  = 7, T  = 3) достигает своего пика при r =  h  /  ( h  +  t ) = 0,7; это значение называется максимальной апостериорной оценкой (MAP) r . Также при равномерном априорном распределении ожидаемое значение r при апостериорном распределении равно

${\displaystyle \operatorname {E} [r]=\int _{0}^{1}r\cdot f(r\mid H=7,T=3)\,\mathrm {d} r={\frac {h+1}{h+t+2}}={\frac {2}{3}}.}$

Оценка истинной вероятности

Используя этот подход, чтобы определить, сколько раз следует подбрасывать монету, требуются два параметра:

1. Уровень достоверности, который обозначается доверительным интервалом (Z)
2. Максимальная (допустимая) погрешность (E)

• Уровень достоверности обозначается как Z и задается значением Z стандартного нормального распределения . Это значение можно прочитать из таблицы статистики стандартных оценок для нормального распределения. Вот несколько примеров:

• Максимальная ошибка (E) определяется как , где — предполагаемая вероятность выпадения орла. Примечание: — та же фактическая вероятность (выпадения орла), что и в предыдущем разделе этой статьи. ${\displaystyle |p-r|<E}$ ${\displaystyle p\,\!}$ ${\displaystyle r}$ ${\displaystyle r\,\!}$
• В статистике оценка доли выборки (обозначаемой p ) имеет стандартную ошибку, определяемую по формуле:

${\displaystyle s_{p}={\sqrt {\frac {p\,(1-p)}{n}}}}$

где n — количество испытаний (которое было обозначено как N в предыдущем разделе).

Эта стандартная функция ошибок p имеет максимум при . Кроме того, в случае подбрасывания монеты, вероятно, что p будет недалеко от 0,5, поэтому разумно принять p = 0,5 в следующем: ${\displaystyle s_{p}}$ ${\displaystyle p=(1-p)=0.5}$

И, следовательно, значение максимальной ошибки (E) определяется как

Решая задачу о необходимом количестве подбрасываний монеты, n ,

${\displaystyle n={\frac {Z^{2}}{4\,E^{2}}}\!}$

Примеры

1. Если желаемая максимальная погрешность составляет 0,01, сколько раз следует подбросить монету?

${\displaystyle n={\frac {Z^{2}}{4\,E^{2}}}={\frac {Z^{2}}{4\times 0.01^{2}}}=2500\ Z^{2}}$

${\displaystyle n=2500\,}$при уровне достоверности 68,27% (Z=1)

${\displaystyle n=10000\,}$при уровне достоверности 95,45% (Z=2)

${\displaystyle n=27225\,}$при уровне достоверности 99,90% (Z=3,3)

2. Если монету подбросить 10000 раз, какова максимальная ошибка оценки значения (фактической вероятности выпадения орла при подбрасывании монеты)? ${\displaystyle p\,\!}$ ${\displaystyle r\,\!}$

${\displaystyle E={\frac {Z}{2\,{\sqrt {n}}}}}$

${\displaystyle E={\frac {Z}{2\,{\sqrt {10000}}}}={\frac {Z}{200}}}$

${\displaystyle E=0.0050\,}$при уровне достоверности 68,27% (Z=1)

${\displaystyle E=0.0100\,}$при уровне достоверности 95,45% (Z=2)

${\displaystyle E=0.0165\,}$при уровне достоверности 99,90% (Z=3,3)

3. Монета подбрасывается 12000 раз, и в результате выпадает 5961 орел (и 6039 решек). В каком интервале лежит значение (истинная вероятность выпадения орла), если желаемый уровень достоверности составляет 99,999%? ${\displaystyle r\,\!}$

${\displaystyle p={\frac {h}{h+t}}\,={\frac {5961}{12000}}\,=0.4968}$

Теперь найдем значение Z, соответствующее уровню достоверности 99,999%.

${\displaystyle Z=4.4172\,\!}$

Теперь вычислите E

${\displaystyle E={\frac {Z}{2\,{\sqrt {n}}}}\,={\frac {4.4172}{2\,{\sqrt {12000}}}}\,=0.0202}$

Интервал, содержащий r, равен:

${\displaystyle p-E<r<p+E\,\!}$

${\displaystyle 0.4766<r<0.5170\,\!}$

Другие подходы

Другие подходы к вопросу проверки честности монеты доступны с использованием теории принятия решений , применение которой потребовало бы формулировки функции потерь или функции полезности , описывающей последствия принятия данного решения. Подход, который избегает необходимости либо функции потерь, либо априорной вероятности (как в байесовском подходе), — это «выборка принятия». ^[2]

Другие приложения

Вышеприведенный математический анализ для определения того, является ли монета честной, может быть применен и в других целях. Например:

• Определение доли дефектных изделий для продукта, подвергаемого определенному (но четко определенному) состоянию. Иногда продукт может быть очень сложным или дорогим в производстве. Кроме того, если тестирование таких продуктов приведет к их разрушению, необходимо протестировать минимальное количество изделий. Используя аналогичный анализ, можно найти функцию плотности вероятности частоты дефектов продукта.
• Двухпартийный опрос. Если проводится небольшой случайный выборочный опрос, где есть только два взаимоисключающих выбора, то это похоже на подбрасывание одной монеты несколько раз, используя, возможно, предвзятую монету. Поэтому аналогичный анализ можно применить для определения уверенности, приписываемой фактическому соотношению поданных голосов. (Если людям разрешено воздержаться , то анализ должен это учитывать, и аналогия с подбрасыванием монеты не совсем верна.)
• Определение соотношения полов в большой группе видов животных. При условии, что при проведении случайной выборки популяции берется небольшая случайная выборка (т.е. малая по сравнению с общей численностью популяции), анализ аналогичен определению вероятности выпадения орла при подбрасывании монеты.

Смотрите также

• Биномиальный тест
• Подбрасывание монеты
• Доверительный интервал
• Теория оценки
• Выводная статистика
• Загруженные кости
• Допустимая погрешность
• Оценка точки
• Статистическая случайность

Ссылки

1. Однако, если монету поймать, а не позволить ей отскочить или вращаться, трудно предвзято повлиять на результат подбрасывания монеты. См. Gelman , Andrew; Deborah Nolan (2002). "Teacher's Corner: You Can Load a Die, But You Can't Bias a Coin". American Statistician . 56 (4): 308–311. doi :10.1198/000313002605. S2CID  123597087.
2. Кокс, DR, Хинкли, DV (1974) Теоретическая статистика (пример 11.7), Chapman & Hall. ISBN 0-412-12420-3 

• Гуттман, Уилкс и Хантер: Вводная инженерная статистика , John Wiley & Sons, Inc. (1971) ISBN 0-471-33770-6 
• Девиндер Сивиа: Анализ данных, байесовский учебник , Oxford University Press (1996) ISBN 0-19-851889-7