
В теории графов кограф , или дополняюще-сводимый граф , или P 4 -свободный граф , — это граф , который может быть сгенерирован из одновершинного графа K 1 с помощью дополнения и несвязного объединения . То есть семейство кографов — это наименьший класс графов, включающий K 1 и замкнутый относительно дополнения и несвязного объединения.
Кографы были открыты независимо несколькими авторами с 1970-х годов; ранние ссылки включают Jung (1978), Lerchs (1971), Seinsche (1974) и Sumner (1974). Их также называли D*-графами , [1] наследственными графами Дейси (в честь связанной работы Джеймса К. Дейси-младшего по ортомодулярным решеткам ), [2] и графами 2-четности . [3] Они имеют простую структурную декомпозицию, включающую операции непересекающегося объединения и дополнения графа , которые могут быть кратко представлены помеченным деревом и использованы алгоритмически для эффективного решения многих задач, таких как поиск максимальной клики , которые сложны для более общих классов графов.
Частные случаи кографов включают полные графы , полные двудольные графы , кластерные графы и пороговые графы . Кографы, в свою очередь, являются частными случаями дистанционно -наследственных графов , графов перестановок , графов сравнимости и совершенных графов .
Любой кограф может быть построен с использованием следующих правил:
Кографы можно определить как графы, которые можно построить с помощью этих операций, начиная с одновершинных графов. [4] В качестве альтернативы, вместо использования операции дополнения можно использовать операцию соединения, которая состоит в формировании непересекающегося объединения и последующем добавлении ребра между каждой парой вершины из и вершины из .
Можно дать несколько альтернативных характеристик кографов. Среди них:
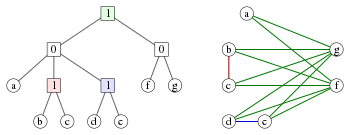
Кодерево — это дерево , в котором внутренние узлы помечены числами 0 и 1. Каждое кодерево T определяет кограф G , имеющий листья T в качестве вершин, и в котором поддерево, корнем которого является каждый узел T, соответствует индуцированному подграфу в G, определяемому набором листьев, исходящих из этого узла:
Эквивалентный способ описания кографа, образованного из кодерева, заключается в том, что две вершины соединены ребром тогда и только тогда, когда наименьший общий предок соответствующих листьев помечен как 1. Наоборот, каждый кограф может быть представлен таким образом кодеревом. Если мы требуем, чтобы метки на любом пути корня-листа этого дерева чередовались между 0 и 1, это представление является уникальным. [4]
Кографы могут быть распознаны за линейное время, и представление кодерева может быть построено с использованием модульной декомпозиции , [9] уточнения разбиения , [10] LexBFS , [11] или разбиения на разделы . [12] После построения представления кодерева многие знакомые проблемы с графами могут быть решены с помощью простых вычислений снизу вверх на кодеревьях.
Например, чтобы найти максимальную клику в кографе, вычислите в порядке снизу вверх максимальную клику в каждом подграфе, представленном поддеревом кодерева. Для узла с меткой 0 максимальная клика является максимальной среди клик, вычисленных для дочерних узлов этого узла. Для узла с меткой 1 максимальная клика является объединением клик, вычисленных для дочерних узлов этого узла, и имеет размер, равный сумме размеров клик дочерних узлов. Таким образом, попеременно максимизируя и суммируя значения, хранящиеся в каждом узле кодерева, мы можем вычислить максимальный размер клики, а попеременно максимизируя и беря объединения, мы можем построить саму максимальную клику. Подобные вычисления дерева снизу вверх позволяют вычислить максимальное независимое множество , число окраски вершин , максимальное покрытие кликой и гамильтоновость (то есть существование гамильтонова цикла ) за линейное время из представления кодерева кографа. [4] Поскольку кографы имеют ограниченную ширину клики, теорему Курселя можно использовать для проверки любого свойства в монадической логике второго порядка графов (MSO 1 ) на кографах за линейное время. [13]
Задача проверки того, находится ли заданный граф на расстоянии k вершин и/или t ребер от кографа, является разрешимой с фиксированными параметрами . [14] Решение вопроса о том, можно ли граф удалить k ребер до кографа, можно решить за O * (2,415 k ) времени, [15] а отредактировать k ребер до кографа — за O * (4,612 k ). [16] Если наибольший индуцированный подграф кографа графа можно найти, удалив k вершин из графа, его можно найти за O * (3,30 k ) времени. [15]
Два кографа изоморфны тогда и только тогда, когда их кодеревья (в канонической форме без двух смежных вершин с одинаковой меткой) изоморфны. Из-за этой эквивалентности можно определить за линейное время, являются ли два кографа изоморфными, построив их кодеревья и применив линейный тест изоморфизма для помеченных деревьев. [4]
Если H является индуцированным подграфом кографа G , то H сам является кографом; кодерево для H может быть сформировано путем удаления некоторых листьев из кодерева для G и последующего подавления узлов, имеющих только одного потомка. Из теоремы Краскала о дереве следует , что отношение быть индуцированным подграфом является хорошо квазиупорядоченным на кографах. [17] Таким образом, если подсемейство кографов (например, планарные кографы) замкнуто относительно операций индуцированного подграфа, то оно имеет конечное число запрещенных индуцированных подграфов . С вычислительной точки зрения это означает, что проверка членства в таком подсемействе может быть выполнена за линейное время с использованием вычисления снизу вверх на кодереве данного графа для проверки того, содержит ли он какой-либо из этих запрещенных подграфов. Однако, когда размеры двух кографов являются переменными, проверка того, является ли один из них индуцированным подграфом другого, является NP-полной . [18]
Кографы играют ключевую роль в алгоритмах распознавания однократно читаемых функций . [19]
Некоторые проблемы подсчета также становятся поддающимися решению, когда входные данные ограничены кографом. Например, существуют полиномиальные алгоритмы для подсчета количества клик или количества максимальных клик в кографе. [4]
Число связных кографов с n вершинами, для n = 1, 2, 3, ..., равно:
При n > 1 существует одинаковое число несвязных кографов, поскольку для каждого кографа ровно один его или его дополнительный граф является связным.
Каждый полный граф K n является кографом, с кодеревом, состоящим из одного 1-узла и n листьев. Аналогично, каждый полный двудольный граф K a , b является кографом. Его кодерево имеет корень в 1-узле, который имеет два потомка 0-узла, один с a листовым потомком и один с b листовыми потомками. Граф Турана может быть образован путем объединения семейства независимых множеств одинакового размера; таким образом, он также является кографом, с кодеревом, имеющим корень в 1-узле, который имеет дочерний 0-узел для каждого независимого множества.
Каждый пороговый граф также является кографом. Пороговый граф может быть сформирован путем многократного добавления одной вершины, либо связанной со всеми предыдущими вершинами, либо ни с одной из них; каждая такая операция является одной из операций непересекающегося объединения или соединения, с помощью которых может быть сформировано кодерево. [20]
Характеристика кографов свойством, что каждая клика и максимальное независимое множество имеют непустое пересечение, является более сильной версией определяющего свойства строго совершенных графов , в которых каждый индуцированный подграф содержит независимое множество, пересекающее все максимальные клики. В кографе каждое максимальное независимое множество пересекает все максимальные клики. Таким образом, каждый кограф строго совершенен. [21]
Тот факт, что кографы являются P 4 -свободными, подразумевает, что они совершенно упорядочиваемы . Фактически, каждый порядок вершин кографа является совершенным порядком, что дополнительно подразумевает, что нахождение максимальной клики и минимальная раскраска могут быть найдены за линейное время с любой жадной раскраской и без необходимости разложения на кодерево.
Каждый кограф является дистанционно-наследственным графом , что означает, что каждый индуцированный путь в кографе является кратчайшим путем . Кографы могут быть охарактеризованы среди дистанционно-наследственных графов как имеющие диаметр не более двух в каждой связной компоненте. Каждый кограф также является графом сравнимости последовательно -параллельного частичного порядка , полученным путем замены операций непересекающегося объединения и соединения, с помощью которых кограф был построен, на операции непересекающегося объединения и порядковой суммы на частичных порядках. Поскольку строго совершенные графы, совершенно упорядочиваемые графы, дистанционно-наследственные графы и графы сравнимости являются совершенными графами , кографы также совершенны. [20]