Комбинаторные виды

В комбинаторной математике теория комбинаторных видов — это абстрактный систематический метод вывода производящих функций дискретных структур, который позволяет не просто подсчитывать эти структуры, но и давать с их участием биективные доказательства . Примерами комбинаторных видов являются (конечные) графы , перестановки , деревья и т. д.; каждому из них соответствует генерирующая функция, которая подсчитывает количество структур определенного размера. Одна из целей теории видов — иметь возможность анализировать сложные структуры, описывая их с точки зрения преобразований и комбинаций более простых структур. Эти операции соответствуют эквивалентным манипуляциям с производящими функциями, поэтому создавать такие функции для сложных структур гораздо проще, чем другими методами. Теория была представлена, тщательно разработана и применена канадскими исследователями во главе с Андре Жойалем .

Сила теории проистекает из ее уровня абстракции. «Формат описания» структуры (например, список смежности или матрица смежности для графов) не имеет значения, поскольку виды являются чисто алгебраическими. Теория категорий обеспечивает полезный язык для возникающих здесь концепций, но не обязательно понимать категории, прежде чем иметь возможность работать с видами.

Категория видов эквивалентна категории симметричных последовательностей в конечных множествах. ^[1]

Определение вида

Схематическая иллюстрация комбинаторной видовой структуры пяти элементов с использованием диаграммы Лабеля.

Любой вид состоит из отдельных комбинаторных структур, построенных на элементах некоторого конечного множества: например, комбинаторный граф — это структура ребер среди заданного множества вершин, а вид графов включает все графы на всех конечных множествах. Более того, базовый набор члена вида может быть перемаркирован элементами любого другого равночисленного набора, например, перемаркировка вершин графа дает «ту же самую структуру графа» на новых вершинах, то есть изоморфный граф .

Это приводит к формальному определению комбинаторного вида . Пусть – категория конечных множеств , причем морфизмы категории являются биекциями между этими множествами. Вид – это функтор ^[2] ${\displaystyle {\mathcal {B}}}$

${\displaystyle F\colon {\mathcal {B}}\to {\mathcal {B}}.}$

Для каждого конечного множества A в , конечное множество F [ A ] ^{[примечание 1]} называется множеством F -структур на A или множеством структур видов F на A . Далее, по определению функтора, если φ — биекция между множествами A и B , то F [φ] — биекция между множествами F -структур F [ A ] и F [ B ], называемая переносом F-структур. структуры вдоль φ . ^[3] ${\displaystyle {\mathcal {B}}}$

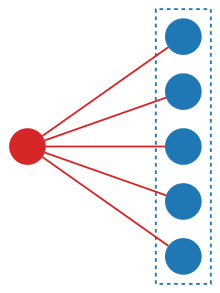
Например, «виды перестановок» ^[4] отображают каждое конечное множество A в множество S [ A ] всех перестановок A (все способы упорядочивания A в список), а каждую биекцию f из A в другое множество B. естественным образом вызывает биекцию (перемаркировку), переводящую каждую перестановку A в соответствующую перестановку B , а именно в биекцию . Аналогично, «виды разделов» могут быть определены путем присвоения каждому конечному набору набора всех его разделов , а «виды наборов мощности» присваиваются каждому конечному множеству его набор мощности . На соседней диаграмме показана структура (представленная красной точкой), построенная на наборе из пяти отдельных элементов (представленных синими точками); соответствующая структура может быть построена из любых пяти элементов. ${\displaystyle S[f]:S[A]\to S[B]}$

Два конечных множества находятся в биекции, если они имеют одинаковую мощность (количество элементов); таким образом, по определению соответствующие множества видов также находятся в биекции, и (конечная) мощность зависит только от мощности A . ^{[примечание 2]} В частности, экспоненциальный порождающий ряд F ( x ) вида F может быть определен: ^[5] ${\displaystyle F[A]}$

${\displaystyle F(x)=\sum _{n\geq 0}\operatorname {Card} F[n]{\frac {x^{n}}{n!}}}$

где – мощность любого множества A, состоящего из n элементов; например, . ${\displaystyle \operatorname {Card} F[n]}$ ${\displaystyle F[A]}$ ${\displaystyle A=\{1,2,\dots ,n\}}$

Несколько примеров: письмо , ${\displaystyle f_{n}=\operatorname {Card} F[n]}$

• Разновидностью множеств (традиционно называемой E , от французского « ансамбля », что означает «множество») является функтор, который отображает A в { A }. Тогда так . ${\displaystyle f_{n}=1}$ ${\displaystyle E(x)=e^{x}}$
• Вид S перестановок , описанный выше, имеет . . ${\displaystyle f_{n}=n!}$ ${\displaystyle S(x)=1/(1-x)}$
• Вид T ₂ упорядоченных пар (2- кортежей ) является функтором, переводящим множество A в A ² . Тогда и . ${\displaystyle f_{n}=n^{2}}$ ${\displaystyle T_{2}(x)=x(x+1)e^{x}}$

Расчет видов

Арифметика производящих функций соответствует определенным «естественным» операциям над видами. Основные операции — сложение, умножение, состав и дифференцирование; необходимо также определить равенство по видам. В теории категорий уже есть способ описания эквивалентности двух функторов: естественный изоморфизм . В этом контексте это просто означает, что для каждого A существует биекция между F -структурами на A и G -структурами на A , которая «хорошо себя ведет» при взаимодействии с транспортом. Виды с одинаковой производящей функцией могут не быть изоморфными, но изоморфные виды всегда имеют одну и ту же производящую функцию.

Добавление

Добавление видов определяется несвязным объединением множеств и соответствует выбору между структурами. ^[6] Для видов F и G определите ( F + G )[ A ] как непересекающееся объединение (также обозначаемое «+») F [ A ] и G [ A ]. Отсюда следует, что ( F  +  G )( x ) =  F ( x ) +  G ( x ). В качестве демонстрации возьмем E ⁺ в качестве вида непустых множеств, производящая функция которых равна E ⁺ ( x ) =  e ^x  − 1, а 1 — в качестве вида пустого множества , производящая функция которого равна 1 ( x ) = 1. Отсюда следует, что сумма двух видов E  =  1  +  E ⁺ : словами, «множество либо пусто, либо непусто». Подобные уравнения можно считать относящимися как к одной структуре, так и ко всему набору структур.

Умножение

Размножение видов немного сложнее. Можно просто взять за определение декартово произведение множеств, но комбинаторная интерпретация этого не совсем верна. (Информацию об использовании такого рода произведения см. ниже.) Вместо того, чтобы объединять две несвязанные структуры в одном множестве, оператор умножения использует идею разделения набора на два компонента, создавая F -структуру из одного и G- . структура с другой. ^[7]

${\displaystyle (F\cdot G)[A]=\sum _{A=B+C}F[B]\times G[C].}$

Это несвязное объединение всех возможных двоичных  разделов A. Несложно показать, что умножение ассоциативно и коммутативно ( с точностью до изоморфизма ) и дистрибутивно по отношению к сложению. Что касается порождающего ряда, ( F  ·  G )( x ) =  F ( x ) G ( x ).

На диаграмме ниже показана одна возможная ( F  ·  G )-структура на множестве из пяти элементов. F - структура (красная) забирает три элемента базового набора, а G -структура (голубая) — остальные. В других структурах F и G будут разделять набор другим способом. Множество ( F  ·  G )[ A ], где A — базовое множество, представляет собой дизъюнктное объединение всех таких структур.

Сложение и умножение видов являются наиболее полным выражением правил счета суммы и произведения. ^{[ нужна цитата ]}

Состав

Композиция , также называемая заменой, снова сложнее. Основная идея состоит в том, чтобы заменить компоненты F на G -структуры, образуя ( F  ∘  G ). ^[8] Как и при умножении, это делается путем разделения входного набора A ; непересекающиеся подмножества передаются G для создания G- структур, а набор подмножеств передается F для создания F -структуры, связывающей G -структуры. Для того чтобы композиция работала, G необходимо сопоставить пустое множество с самим собой. Формальное определение:

${\displaystyle (F\circ G)[A]=\sum _{\pi \in P[A]}(F[\pi ]\times \prod _{B\in \pi }G[B]).}$

Здесь P — вид разделов, поэтому P [ A ] — набор всех разделов A. Это определение говорит, что элемент ( F  ∘  G )[ A ] состоит из F -структуры на некотором разбиении A и G -структуры на каждом компоненте разбиения. Производящий ряд – это . ${\displaystyle (F\circ G)(x)=F(G(x))}$

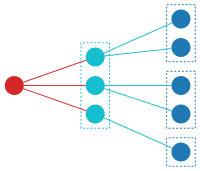
Одна из таких структур показана ниже. Три G -структуры (голубые) делят между собой базовый набор из пяти элементов; затем строится F -структура (красная) для соединения G -структур.

Эти последние две операции можно проиллюстрировать на примере деревьев. Во-первых, определите X как вид «одиночки», порождающий ряд которого равен X ( x ) =  x . Тогда вид Ar корневых деревьев (от французского « древесность ») определяется рекурсивно как Ar  =  X  ·  E ( Ar ). Это уравнение говорит, что дерево состоит из одного корня и набора (под)деревьев. Рекурсия не требует явного базового варианта: она генерирует деревья только в контексте применения к некоторому конечному множеству. Один из способов подумать об этом состоит в том, что функтор Ar неоднократно применяется к «поставке» элементов из набора — каждый раз один элемент берется X , а остальные распределяются E среди поддеревьев Ar , пока не больше нет элементов для передачи E . Это показывает, что алгебраические описания видов сильно отличаются от спецификаций типов в таких языках программирования, как Haskell .

Аналогично, вид P можно охарактеризовать как P  =  E ( E ⁺ ): «раздел — это попарно непересекающееся множество непустых множеств (использующих все элементы входного набора)». Экспоненциальный производящий ряд для P равен ряду для чисел Белла . ${\displaystyle P(x)=e^{(e^{x}-1)}}$

Дифференциация

Дифференциация видов интуитивно соответствует построению «конструкций с дыркой», как показано на иллюстрации ниже.

Формально ^[9]

${\displaystyle (F')[A]=F[A\uplus \{\star \}],}$

где какой-то выдающийся новый элемент, которого нет в . ${\displaystyle \star }$ ${\displaystyle A}$

Чтобы дифференцировать связанный с ним показательный ряд, последовательность коэффициентов необходимо сдвинуть на одно место «влево» (теряя первый член). Это предполагает определение вида: F' [ A ] =  F [ A  + {*}], где {*} — одноэлементное множество, а «+» — непересекающееся объединение. Более продвинутые части теории видов широко используют дифференцирование для построения и решения дифференциальных уравнений для видов и серий. Идея добавления (или удаления) отдельной части структуры является мощной: ее можно использовать для установления отношений между, казалось бы, не связанными друг с другом видами.

Например, рассмотрим структуру вида L линейных порядков — списков элементов основного множества. Удаление элемента списка разбивает его на две части (возможно, пустые); в символах это L'  =  L · L. Экспоненциальная производящая функция L равна L ( x ) = 1/(1 −  x ), и действительно:

${\displaystyle {\frac {d}{dx}}{(1-x)}^{-1}={(1-x)}^{-2}.}$

Формулы обобщенного дифференцирования можно найти в предыдущем исследовании Н. Г. де Брейна, опубликованном в 1964 году.

Вид C циклических перестановок переводит набор A в набор всех циклов на A . Удаление одного элемента из цикла сводит его к списку: C '  =  L. Мы можем интегрировать производящую функцию L , чтобы получить ее для  C.

${\displaystyle C(x)=1+\int _{0}^{x}{\frac {dt}{1-t}}=1+\log {\frac {1}{1-x}}.}$

Хорошим примером интеграции вида является завершение линии (координируемой полем) бесконечной точкой и получение проективной линии.

Дальнейшие операции

Существует множество других манипуляций, которые можно проводить с видами. Они необходимы для выражения более сложных структур, таких как ориентированные графы или биграфы .

При наведении указателя выделяется один элемент в структуре. ^[10] Учитывая вид F , соответствующий заостренный вид F ^• определяется как F ^• [ A ] = A × F [ A ]. Таким образом, каждая F ^• -структура является F -структурой с одним выделенным элементом. Указание связано с дифференцированием соотношением F ^• = X · F' , поэтому F ^• ( x ) = x F' ( x ). Вид заостренных множеств E ^• особенно важен как строительный блок для многих более сложных конструкций.

Декартово произведение двух видов — это вид, который может одновременно строить две структуры на одном и том ^{же множестве .} Он отличается от обычного оператора умножения тем, что все элементы базового набора являются общими для двух структур. ( F × G )-структуру можно рассматривать как суперпозицию F -структуры и G -структуры. Биграфы можно описать как суперпозицию графа и набора деревьев: каждый узел биграфа является частью графа и в то же время частью некоторого дерева, которое описывает вложенность узлов. Производящая функция ( F × G )( x ) представляет собой произведение Адамара или по коэффициентам F ( x ) и G ( x ).

Вид E ^• × E ^• можно рассматривать как производящий два независимых выбора из базового набора. Две точки могут совпадать, в отличие от X · X · E , где они вынуждены быть разными.

В качестве функторов виды F и G могут быть объединены посредством функториальной композиции : ^{[ нужна ссылка ]} (используется символ прямоугольника, поскольку круг уже используется для замены). Это создает F -структуру на множестве всех G -структур на множестве A. Например, если F — функтор, переводящий набор в его степенное множество, структура составного вида — это некоторое подмножество G -структур на A . Если теперь мы возьмем G равным E ^• × E ^• сверху, мы получим вид ориентированных графов с разрешенными циклами. (Ориентированный граф — это набор ребер, а ребра — это пары узлов: поэтому граф — это подмножество множества пар элементов набора узлов A. ) Другие семейства графов, а также многие другие структуры могут определить таким образом. ${\displaystyle (F\,\Box \,G)[A]=F[G[A]]}$

Программное обеспечение

Операции с видами поддерживаются SageMath ^[11] и, при использовании специального пакета, еще и Haskell . ^{[12] [13]}

Варианты

• Вид в k сортах является функтором . Здесь создаваемые структуры могут содержать элементы, взятые из разных источников. ^{[ нужна цитата ]} ${\displaystyle {\mathcal {B}}^{k}\rightarrow {\mathcal {B}}}$
• Функтор to , категория R -взвешенных множеств для R, кольца степенных рядов , является взвешенным видом . ^{[ нужна цитата ]} ${\displaystyle {\mathcal {B}}_{R}}$

Если «конечные множества с биекциями» заменить на «конечные векторные пространства с линейными преобразованиями», то получится понятие полиномиального функтора (после наложения некоторого условия конечности). ^{[ нужна цитата ]}

Смотрите также

• Контейнер (теория типов)

Примечания

1. Джоял предпочитает писать для значения F в A. ${\displaystyle F[A]}$ ${\displaystyle F(A)}$
2. Если это биекция, то это биекция и, следовательно, имеет ту же мощность. ${\displaystyle u:A\to B}$ ${\displaystyle F[u]:F[A]\to F[B]}$ ${\displaystyle F[A],F[B]}$

1. Симметричная последовательность в n Lab
2. Джоял 1981, § 1.1. Определение 1.
3. Федерико Г. Ластария, Приглашение к комбинаторным видам. (2002)
4. Джоял 1981, § 1.1. Пример 3.
5. Джоял 1981, § 1.1.1.
6. Джоял 1981, § 2.1.
7. Джоял 1981, § 2.1. Определение 5
8. Джоял 1981, § 2.2. Определение 7
9. Джоял 1981, § 2.3. Определение 8
10. Флажоле, Филипп ; Седжвик, Роберт (2009). Аналитическая комбинаторика .
11. Документация Sage по комбинаторным видам.
12. Виды пакетов Haskell.
13. Брент А., Йорги (2010). «Виды, функторы и типы, о боже!». Материалы третьего симпозиума ACM Haskell по Haskell-Haskell '10 . АКМ. стр. 147–158. CiteSeerX 10.1.1.165.6421 . дои : 10.1145/1863523.1863542. ISBN  978-1-4503-0252-4. S2CID  511418.

Рекомендации

• Джоял, Андре (октябрь 1981 г.). «Комбинированная теория серий форм». Достижения в математике . 42 (1): 1–82. дои : 10.1016/0001-8708(81)90052-9.
• Брюйн, де, Н.Г. (1964). Теория счета Пойа. В EF Beckenbach (Ed.), Прикладная комбинаторная математика (стр. 144-184).
• Лабель, Жак. Некоторые особенные ансамбли миниатюрных кардиналов. , Анна. наук. Математика. Квебек 9.1 (1985): 31–58.
• Лабелль, Дж.; Да, Ю.Н. (1989). «Связь между кольцами Бернсайда и комбинаторными видами». Журнал комбинаторной теории . Серия А. 50 (2): 269–284. дои : 10.1016/0097-3165(89)90019-8 .
• Ив Чирикота, Классификация особенных молекул 6 и 7 степени , Ann. наук. Математика. Квебек 17 (1993), вып. 1, 11–37.
• Франсуа Бержерон, Жильбер Лабель, Пьер Леру, Теория особенных и комбинационных структур древесных пород , LaCIM, Монреаль (1994). Английская версия: Комбинаторные виды и древовидные структуры. Архивировано 2 октября 2006 г. в Wayback Machine , Cambridge University Press (1998).
• Кербер, Адальберт (1999), Прикладные действия конечных групп, Алгоритмы и комбинаторика, 19 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-65941-9 , MR 1716962, OCLC 247593131 

Внешние ссылки

• Вайсштейн, Эрик В. «Виды». Математический мир .
• виды в лаборатории n