В геометрии Коксетер назвал правильный многогранник особым видом конфигурации .
Другие конфигурации в геометрии — это нечто иное. Эти конфигурации многогранников можно точнее назвать матрицами инцидентности , где подобные элементы собираются вместе в строках и столбцах. Правильные многогранники будут иметь одну строку и столбец на элемент k -грани , в то время как другие многогранники будут иметь одну строку и столбец для каждого типа k-грани по их классам симметрии. Многогранник без симметрии будет иметь одну строку и столбец для каждого элемента, и матрица будет заполнена 0, если элементы не связаны, и 1, если они связаны. Элементы с одинаковым k не будут связаны и будут иметь запись в таблице "*". [1]
Каждый многогранник и абстрактный многогранник имеет диаграмму Хассе , выражающую эти связности, которые можно систематически описать с помощью матрицы инцидентности .
Конфигурация правильного многогранника представлена матрицей, где диагональный элемент, N i , является числом i -граней в многограннике. Диагональные элементы также называются f-вектором многогранника . Недиагональный ( i ≠ j ) элемент N ij является числом j -граней, инцидентных каждому элементу i -грани, так что N i N ij = N j N ji . [2]
Этот принцип распространяется в целом на n измерений, где 0 ≤ j < n .
Правильный многоугольник , символ Шлефли { q }, будет иметь матрицу 2x2, с первой строкой для вершин и второй строкой для ребер. Порядок g равен 2 q .
Обычный n-угольник будет иметь матрицу 2n x 2n, в которой первые n строк и столбцов являются вершинами, а последние n строк и столбцов — ребрами.
Существует три классификации симметрии треугольника : равносторонний, равнобедренный и разносторонний. Все они имеют одинаковую матрицу инцидентности , но симметрия позволяет собирать вершины и ребра вместе и подсчитывать их. Эти треугольники имеют вершины, обозначенные как A, B, C, и ребра, обозначенные как a, b, c, в то время как вершины и ребра, которые могут быть отображены друг на друга с помощью операции симметрии, обозначены одинаково.

Четырехугольники можно классифицировать по симметрии, каждый со своей собственной матрицей. Четырехугольники существуют с дуальными парами, которые будут иметь ту же матрицу, повернутую на 180 градусов, с перевернутыми вершинами и ребрами. Квадраты и параллелограммы, а также общие четырехугольники являются самодуальными по классу, поэтому их матрицы не меняются при повороте на 180 градусов.
Идея применима также для правильных сложных многоугольников , p { q } r построенных в :
Группа комплексного отражения имеет порядок p [ q ] r . [3] [ 4]
Эту идею можно применить в трех измерениях, рассматривая инцидентности точек, линий и плоскостей или j -пространств (0 ≤ j < 3) , где каждое j -пространство инцидентно N jk k -пространствам ( j ≠ k ) . Записывая N j для числа присутствующих j -пространств, заданную конфигурацию можно представить матрицей
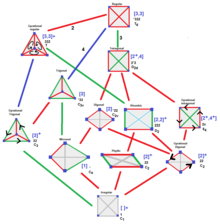
Тетраэдры имеют матрицы, которые также могут быть сгруппированы по их симметрии, с общим тетраэдром, имеющим 14 строк и столбцов для 4 вершин, 6 ребер и 4 граней. Тетраэдры являются самодвойственными, и поворот матрикса на 180 градусов (перестановка вершин и граней) оставит его неизменным.