Коррелированная цветовая температура

Свойство света, основанное на восприятии человека

Логарифмические графики пиковой длины волны излучения и светимости в зависимости от температуры черного тела , нанесенные на синюю линию. Красные стрелки показывают, что черные тела с температурой 5780 К имеют пиковую длину волны 501 нм и светимость 63,3 МВт/м ^{2 .}

Коррелированная цветовая температура ( CCT , T _cp ) относится к температуре планковского излучателя , воспринимаемый цвет которого наиболее близок к цвету данного стимула при той же яркости и в определенных условиях просмотра." ^{[1] [2]}

Мотивация

Излучатели черного тела являются эталоном, по которому судят о белизне источников света. Черное тело характеризуется своей температурой и излучает свет определенного оттенка, который называется цветовой температурой . ^{[3] [4] [5]} На практике источники света, которые приближаются к планковским излучателям, такие как некоторые люминесцентные или высокоинтенсивные разрядные лампы, оцениваются на основе их CCT, которая является температурой планковского излучателя, цвет которого наиболее близок к цвету источника света. Для источников света, которые не следуют планковскому распределению, выравнивание их с черным телом не является простым; таким образом, концепция CCT расширена, чтобы представить эти источники как можно точнее на одномерной шкале цветовой температуры, где «как можно точнее» определяется в рамках объективного цветового пространства.

Фон

Диаграмма Джадда (r,g). Концентрические кривые указывают на локусы постоянной чистоты .

Треугольник Максвелла Джадда. Планковское геометрическое место точек выделено серым цветом. Переход от трилинейных координат к декартовым приводит к следующей диаграмме.

Равномерное пространство цветности Джадда (UCS) с планковским геометрическим местом и изотермами от 1000 К до 10000 К, перпендикулярными геометрическому месту. Джадд вычислил изотермы в этом пространстве, прежде чем перевести их обратно в пространство цветности (x,y), как показано на диаграмме в верхней части статьи.

Крупный план локуса Планка в CIE 1960 UCS с изотермами в майредах . Обратите внимание на равномерное расположение изотерм при использовании обратной температурной шкалы и сравните с аналогичным рисунком ниже. Равномерное расположение изотерм на локусе означает, что шкала майредов является лучшим показателем перцептивной цветовой разницы, чем температурная шкала.

Идея использования планковских излучателей в качестве критерия, по которому можно судить о других источниках света, не нова. ^[6] В 1923 году, описывая «классификацию источников света по качеству цвета... температуру источника как показатель качества цвета», Прист по сути описал КЦТ так, как мы понимаем ее сегодня, зайдя так далеко, что стал использовать термин «кажущаяся цветовая температура», и проницательно распознал три случая: ^[7]

• «Те, для которых спектральное распределение энергии идентично тому, которое дается формулой Планка».
• «Те, для которых спектральное распределение энергии не идентично тому, которое дается формулой Планка, но все же имеет такую ​​форму, что качество вызываемого цвета такое же, как и то, которое было бы вызвано энергией от излучателя Планка при данной цветовой температуре».
• «Те, для которых спектральное распределение энергии таково, что цвет может быть сопоставлен лишь приблизительно с помощью стимула планковской формы спектрального распределения».

В 1931 году произошло несколько важных событий. В хронологическом порядке:

1. Рэймонд Дэвис опубликовал статью о «коррелированной цветовой температуре» (его термин). Ссылаясь на планковское локус на rg-диаграмме, он определил CCT как среднее значение «температур первичного компонента» (RGB CCT), используя трилинейные координаты . ^[8]
2. CIE объявила о цветовом пространстве XYZ .
3. Дин Б. Джадд опубликовал статью о природе « наименее заметных различий » в отношении хроматических стимулов. Эмпирическим путем он определил, что разница в ощущении, которую он назвал ΔE для «дискриминационного шага между цветами... Empfindung » (нем. для ощущения), была пропорциональна расстоянию между цветами на диаграмме цветности. Ссылаясь на диаграмму цветности (r,g), изображенную сбоку, он выдвинул гипотезу, что ^[9]

К Δ Е знак равно | с ₁ - с ₂ | = max(| р ₁ - р ₂ |, | г ₁ - г ₂ |).

Эти разработки проложили путь к разработке новых пространств цветности, которые больше подходят для оценки коррелированных цветовых температур и различий цветности. Объединяя понятия разницы цвета и цветовой температуры, Прист сделал наблюдение, что глаз чувствителен к постоянным различиям в «обратной» температуре: ^[10]

Разница в один микрообратный градус (мкрд) является достаточно репрезентативной для сомнительно заметной разницы при самых благоприятных условиях наблюдения.

Прист предложил использовать «шкалу температур как шкалу для упорядочивания цветностей нескольких источников света в последовательном порядке». В течение следующих нескольких лет Джадд опубликовал еще три значимых статьи:

Первая часть подтвердила выводы Приста ^[7] , Дэвиса ^[8] и Джадда ^[9] в статье о чувствительности к изменению цветовой температуры. ^[11]

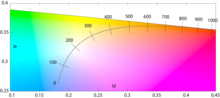
Второй предложил новое пространство цветности, руководствуясь принципом, который стал святым Граалем цветовых пространств: перцептуальная однородность (расстояние цветности должно быть соизмеримо с перцептуальной разницей). С помощью проективного преобразования Джадд нашел более «равномерное пространство цветности» (UCS), в котором можно найти CCT. Джадд определил «ближайшую цветовую температуру», просто найдя точку на локусе Планка, ближайшую к цветности стимула на цветовом треугольнике Максвелла , изображенном сбоку. Матрица преобразования, которую он использовал для преобразования трехцветных значений X, Y, Z в координаты R, G, B, была: ^[12]

${\displaystyle {\begin{bmatrix}R\\G\\B\end{bmatrix}}={\begin{bmatrix}3.1956&2.4478&-0.1434\\-2.5455&7.0492&0.9963\\0.0000&0.0000&1.0000\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}.}$

Отсюда можно найти следующие цветности: ^[13]

${\displaystyle u={\frac {0.4661x+0.1593y}{y-0.15735x+0.2424}},\quad v={\frac {0.6581y}{y-0.15735x+0.2424}}.}$

Третий вариант изображал геометрическое место изотермических хроматичностей на диаграмме цветности CIE 1931 x, y . ^[14] Поскольку изотермические точки образовывали нормали на его диаграмме UCS, преобразование обратно в плоскость xy показало, что они по-прежнему являются линиями, но уже не перпендикулярны геометрическому месту.

Расчет

Диаграмма «равномерной шкалы цветности» МакАдама; упрощение UCS Джадда.

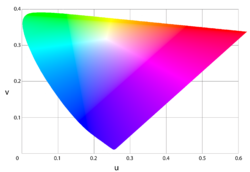
Идея Джадда об определении ближайшей точки к планковскому локусу на однородном пространстве цветности является актуальной. В 1937 году МакАдам предложил «модифицированную диаграмму однородной шкалы цветности», основанную на некоторых упрощающих геометрических соображениях: ^[15]

${\displaystyle u={\frac {4x}{-2x+12y+3}},\quad v={\frac {6y}{-2x+12y+3}}.}$

Это (u,v) пространство цветности стало цветовым пространством CIE 1960 , которое до сих пор используется для расчета CCT (хотя МакАдам и не разрабатывал его с этой целью). ^[16] Использование других пространств цветности, таких как u'v' , приводит к нестандартным результатам, которые, тем не менее, могут быть перцептивно значимыми. ^[17]

Крупный план CIE 1960 UCS . Изотермы перпендикулярны планковскому локусу и показаны для указания максимального расстояния от локуса, на котором CIE считает коррелированную цветовую температуру значимой: Δ _uv = ± 0,05

Расстояние от локуса (т.е. степень отклонения от черного тела) традиционно указывается в единицах Δ _uv ; положительно для точек выше локуса. Эта концепция расстояния развилась в CIELAB ΔE* , которая продолжает использоваться и сегодня.

Метод Робертсона

До появления мощных персональных компьютеров было принято оценивать коррелированную цветовую температуру путем интерполяции из справочных таблиц и диаграмм. ^[18] Наиболее известным таким методом является метод Робертсона, ^[19] который использовал относительно равномерное расположение шкалы майреда (см. выше) для расчета CCT T _c с помощью линейной интерполяции значений майреда изотермы: ^[20]

Вычисление CCT T _{c ,} соответствующей координате цветности в CIE 1960 UCS. ${\displaystyle \scriptstyle (u_{T},v_{T})}$

${\displaystyle {\frac {1}{T_{c}}}={\frac {1}{T_{i}}}+{\frac {\theta _{1}}{\theta _{1}+\theta _{2}}}\left({\frac {1}{T_{i+1}}}-{\frac {1}{T_{i}}}\right),}$

где и — цветовые температуры искомых изотерм, а i выбирается таким образом, что . (Более того, тестовая цветность лежит между единственными двумя соседними линиями, для которых .) ${\displaystyle T_{i}}$ ${\displaystyle T_{i+1}}$ ${\displaystyle T_{i}<T_{c}<T_{i+1}}$ ${\displaystyle d_{i}/d_{i+1}<0}$

Если изотермы достаточно плотные, можно предположить , что приводит к ${\displaystyle \theta _{1}/\theta _{2}\approx \sin \theta _{1}/\sin \theta _{2}}$

${\displaystyle {\frac {1}{T_{c}}}={\frac {1}{T_{i}}}+{\frac {d_{i}}{d_{i}-d_{i+1}}}\left({\frac {1}{T_{i+1}}}-{\frac {1}{T_{i}}}\right).}$

Расстояние от точки испытания до i -й изотермы определяется по формуле

${\displaystyle d_{i}={\frac {(v_{T}-v_{i})-m_{i}(u_{T}-u_{i})}{\sqrt {1+m_{i}^{2}}}},}$

где - координата цветности i -й изотермы на локусе Планка, а m _i - наклон изотермы . Поскольку она перпендикулярна локусу, следует, что где l _i - наклон локуса в . ${\displaystyle (u_{i},v_{i})}$ ${\displaystyle m_{i}=-1/l_{i}}$ ${\displaystyle (u_{i},v_{i})}$

Меры предосторожности

Хотя КЦТ можно рассчитать для любой координаты цветности, результат имеет смысл только в том случае, если источник света в некоторой степени приближается к планковскому излучателю . ^[21] CIE рекомендует, чтобы «концепция коррелированной цветовой температуры не использовалась, если цветность тестового источника отличается от планковского излучателя более чем на Δ _uv = 5×10 ^{-2 ». [22]} За пределами определенного значения Δ _uv координата цветности может быть равноудалена от двух точек на локусе, что приводит к неоднозначности в КЦТ.

Приближение

Если рассматривать узкий диапазон цветовых температур — наиболее практичным случаем является дневной свет — можно аппроксимировать планковское локусное место, чтобы рассчитать CCT в терминах координат цветности. Следуя наблюдению Келли, что изотермы пересекаются в фиолетовой области около ( x = 0,325, y = 0,154), ^[18] МакКами предложил следующее кубическое приближение: ^[23]

${\displaystyle CCT(x,y)=-449n^{3}+3525n^{2}-6823.3n+5520.33,}$

где n = ( x − x _e )/( y - y _e ) — обратная наклонная линия, а ( x _e = 0,3320, y _e = 0,1858) — «эпицентр»; довольно близко к точке пересечения, упомянутой Келли. Максимальная абсолютная погрешность для цветовых температур в диапазоне от 2856 К (источник света A) до 6504 К ( D65 ) составляет менее 2 К.

Предложение Эрнандеса-Андре 1999 года, использующее экспоненциальные члены, значительно расширяет применимый диапазон, добавляя второй эпицентр для высоких цветовых температур: ^[24]

${\displaystyle CCT(x,y)=A_{0}+A_{1}\exp(-n/t_{1})+A_{2}\exp(-n/t_{2})+A_{3}\exp(-n/t_{3})}$

где n такое же, как и прежде, а другие константы определены ниже:

Автор предлагает использовать уравнение для низких температур, чтобы определить, необходимы ли параметры для более высоких температур.

Ohno (2013) предлагает точный комбинированный метод, основанный на таблице поиска, «параболическом» поиске и «треугольном» поиске. В статье подчеркивается важность возврата значения Δ _uv для оценки источников света. ^[25] Поскольку он не использует одну фиксированную таблицу, его можно применять к любой функции сопоставления цветов наблюдателя. ^[26]

Обратный расчет, от цветовой температуры до соответствующих координат цветности, обсуждается в разделе Планковское место точек § Аппроксимация .

Ссылки

1. Международный словарь по освещению CIE/IEC 17.4:1987 Архивировано 27 февраля 2010 г. на Wayback Machine ( ISBN  3900734070 )
2. Борбели, Акос; Самсон, Арпад; Шанда, Янош (декабрь 2001 г.). «Возвращение к концепции коррелированной цветовой температуры». Исследование и применение цвета . 26 (6): 450–457. дои : 10.1002/col.1065. Архивировано из оригинала 5 февраля 2009 г.
3. "The Color White". Architect Magazine . 19 марта 2007 г. Получено 16 июля 2024 г.
4. "Что такое CCT?". Anova Lighting . 30 мая 2024 г. Получено 16 июля 2024 г.
5. "Влияние освещенности и коррелированной цветовой температуры внутреннего освещения на восприятие эмоций". Nature . 12 июля 2021 г. . Получено 16 июля 2024 г. .
6. Hyde, Edward P. (июнь 1911 г.). "Новое определение селективного излучения тантала (аннотация)". Physical Review . Серия I. 32 (6). Американское физическое общество: 632–633. doi :10.1103/PhysRevSeriesI.32.632. Это существование цветового соответствия является следствием приблизительно одинакового распределения энергии в видимых спектрах.
7. Priest, Irwin G. (1923). "Колориметрия и фотометрия дневного света и ламп накаливания методом вращательной дисперсии". JOSA . 7 (12): 1175–1209. Bibcode :1923JOSA....7.1175P. doi :10.1364/JOSA.7.001175. Цветовая температура источника - это температура, при которой планковский излучатель будет испускать лучистую энергию, способную вызвать цвет того же качества, что и вызванный лучистой энергией из рассматриваемого источника . Цветовая температура не обязательно совпадает с "истинной температурой" источника; но это обстоятельство не имеет никакого значения при использовании цветовой температуры в качестве средства для цели установления шкалы качества цвета источников света. Для этой цели не требуется знания температуры источника или даже его излучательных свойств. Все, что требуется для указания цветовой температуры любого источника света, это утверждение, что цвет источника света имеет то же качество, что и цвет планковского излучателя при данной температуре .
8. Davis, Raymond (1931). "Коррелированная цветовая температура для источников света". Bureau of Standards Journal of Research . 7 (4): 659–681. doi : 10.6028/jres.007.039 . Идеальная коррелированная цветовая температура источника света — это абсолютная температура, при которой планковский излучатель испускает компонент лучистой энергии, чтобы вызвать цвет, который из всех планковских цветов наиболее близко приближается к цвету, вызываемому рассматриваемым источником.из исследовательской работы 365
9. Джадд, Дин Б. (1931). «Чувствительность цветности к различиям стимулов». JOSA . 22 (2): 72–108. doi :10.1364/JOSA.22.000072.
10. Прист, Ирвин Г. (февраль 1933 г.). «Предлагаемая шкала для использования при указании цветности ламп накаливания и различных фаз дневного света». JOSA . 23 (2): 42. Bibcode :1933JOSA...23...41P. doi :10.1364/JOSA.23.000041.
11. Джадд, Дин Б. (январь 1933 г.). «Чувствительность к изменению цветовой температуры как функция температуры». JOSA . 23 (1): 7. Bibcode :1933JOSA...23....7J. doi :10.1364/JOSA.23.000007. Относительно (Дэвис, 1931 г.): Это более простое утверждение о спектрально-центроидной связи могло быть выведено путем объединения двух предыдущих открытий, одно из которых было сделано Гибсоном (см. сноску 10, стр. 12) относительно спектрально-центроидной связи между падающим и прошедшим светом для фильтров дневного света, другое — Ленгмюром и Оранжем (Trans. AIEE, 32, 1944–1946 (1913)) относительно аналогичной связи, включающей обратную температуру. Математический анализ, на котором основано это последнее открытие, был дан позднее Футом, Молером и Фэрчайлдом, J. Washington Acad. Sci. 7, 545–549 (1917), и Гейджем, Trans. IES 16, 428–429 (1921), также обратившими внимание на эту связь.
12. Джадд, Дин Б. (январь 1935 г.). "Треугольник Максвелла, дающий шкалы однородной цветности" (PDF) . JOSA . 25 (1): 24–35. Bibcode :1935JOSA...25...24J. doi :10.1364/JOSA.25.000024. Архивировано (PDF) из оригинала 2017-01-30. Важное применение этой системы координат — ее использование для поиска из любой серии цветов одного, наиболее похожего на соседний цвет той же яркости, например, для поиска ближайшей цветовой температуры для соседнего непланковского стимула. Метод заключается в проведении кратчайшей линии от точки, представляющей непланковский стимул, до планковского локуса.
13. Комитет OSA по колориметрии (ноябрь 1944 г.). «Количественные данные и методы колориметрии». JOSA . 34 (11): 633–688. Bibcode :1944JOSA...34..633C. doi :10.1364/JOSA.34.000633.(рекомендуется к прочтению)
14. Джадд, Дин Б. (ноябрь 1936 г.). «Оценка различий в цветности и ближайших цветовых температур в стандартной колориметрической системе координат ICI 1931 г.» (PDF) . JOSA . 26 (11): 421–426. Bibcode :1936JOSA...26..421J. doi :10.1364/JOSA.26.000421. Архивировано (PDF) из оригинала 2017-02-11.
15. МакАдам, Дэвид Л. (август 1937 г.). «Проективные преобразования цветовых характеристик ICI». ДЖОСА . 27 (8): 294–299. Бибкод : 1937JOSA...27..294M. дои : 10.1364/JOSA.27.000294.
16. Определение коррелированной цветовой температуры CIE (удалено) Архивировано 2009-02-05 на Wayback Machine
17. Шанда, Янош; Дани, М. (1977). «Расчеты коррелированной цветовой температуры в диаграмме цветности CIE 1976». Color Research & Application . 2 (4). Wiley Interscience : 161–163. doi :10.1002/col.5080020403. Коррелированную цветовую температуру можно рассчитать с помощью новой диаграммы, что приводит к несколько иным результатам, чем те, которые рассчитаны в соответствии с диаграммой УФ CIE 1960.
18. Келли, Кеннет Л. (август 1963 г.). «Линии постоянной коррелированной цветовой температуры на основе преобразования однородной хроматичности Мак-Адама (u,v) диаграммы CIE». JOSA . 53 (8): 999–1002. Bibcode :1963JOSA...53..999K. doi :10.1364/JOSA.53.000999.
19. Робертсон, Алан Р. (ноябрь 1968 г.). «Вычисление коррелированной цветовой температуры и температуры распределения». JOSA . 58 (11): 1528–1535. Bibcode :1968JOSA...58.1528R. doi :10.1364/JOSA.58.001528.
20. Реализация ANSI C Архивировано 22 апреля 2008 г. на Wayback Machine , Брюс Линдблум
21. Вальтер, Вольфганг (февраль 1992 г.). «Определение коррелированной цветовой температуры на основе модели цветового восприятия». Color Research & Application . 17 (1): 24–30. doi :10.1002/col.5080170107. Концепция коррелированной цветовой температуры полезна только для ламп с точками цветности, близкими к черному телу...
22. Шанда, Янош (2007). "3: CIE Colorimetry". Колориметрия: понимание системы CIE . Wiley Interscience . стр. 37–46. doi :10.1002/9780470175637.ch3. ISBN 978-0-470-04904-4.
23. МакКами, Кэлвин С. (апрель 1992 г.). «Коррелированная цветовая температура как явная функция координат цветности». Color Research & Application . 17 (2): 142–144. doi :10.1002/col.5080170211.плюс ошибка : 10.1002/col.5080180222
24. Эрнандес-Андрес, Хавьер; Ли, Р. Л.; Ромеро, Дж. (20 сентября 1999 г.). «Расчет коррелированных цветовых температур по всему диапазону дневного и небесного освещения» (PDF) . Прикладная оптика . 38 (27): 5703–5709. Bibcode :1999ApOpt..38.5703H. doi :10.1364/AO.38.005703. PMID  18324081. Архивировано (PDF) из оригинала 1 апреля 2016 г.
25. Ohno, Yoshi (2 января 2014 г.). «Практическое использование и расчет CCT и Duv». LEUKOS . 10 (1): 47–55. doi :10.1080/15502724.2014.839020. S2CID  122251872.
26. "colour.temperature.uv_to_CCT_Ohno2013 — Документация по Color 0.4.4". colour.readthedocs.io .