Вырожденные уровни энергии

Уровень энергии квантовой системы, соответствующий двум или более различным измеримым состояниям

В квантовой механике уровень энергии вырожден , если он соответствует двум или более различным измеримым состояниям квантовой системы . И наоборот, два или более различных состояния квантово-механической системы называются вырожденными, если они дают одинаковое значение энергии при измерении. Число различных состояний, соответствующих определенному уровню энергии, известно как степень вырождения (или просто вырожденность ) уровня. Математически он представлен гамильтонианом для системы, имеющей более одного линейно независимого собственного состояния с одинаковым собственным значением энергии . ^{[1] : 48} Когда это так, одной энергии недостаточно, чтобы охарактеризовать, в каком состоянии находится система, и необходимы другие квантовые числа , чтобы охарактеризовать точное состояние, когда требуется различие. В классической механике это можно понять в терминах различных возможных траекторий, соответствующих одной и той же энергии.

Вырождение играет фундаментальную роль в квантовой статистической механике . Для системы из N частиц в трех измерениях один уровень энергии может соответствовать нескольким различным волновым функциям или энергетическим состояниям. Все эти вырожденные состояния на одном уровне имеют одинаковую вероятность быть заполненными. Число таких состояний дает вырождение конкретного уровня энергии.

Вырожденные состояния в квантовой системе

Математика

Возможные состояния квантово-механической системы можно математически рассматривать как абстрактные векторы в сепарабельном комплексном гильбертовом пространстве , в то время как наблюдаемые могут быть представлены линейными эрмитовыми операторами, действующими на них. Выбрав подходящий базис , можно определить компоненты этих векторов и матричные элементы операторов в этом базисе. Если A — матрица N  ×  N , X — ненулевой вектор , а λ — скаляр , такой что , то скаляр λ называется собственным значением A , а вектор X — собственным вектором, соответствующим λ . Вместе с нулевым вектором множество всех собственных векторов, соответствующих данному собственному значению λ, образуют подпространство C ⁿ , которое называется собственным пространством λ . Собственное значение λ, которое соответствует двум или более различным линейно независимым собственным векторам, называется вырожденным , т. е. и , где и являются линейно независимыми собственными векторами. Размерность собственного пространства, соответствующего этому собственному значению, называется степенью его вырождения , которая может быть конечной или бесконечной. Собственное значение называется невырожденным, если его собственное пространство одномерно. ${\displaystyle AX=\lambda X}$ ${\displaystyle AX_{1}=\lambda X_{1}}$ ${\displaystyle AX_{2}=\lambda X_{2}}$ ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$

Собственные значения матриц, представляющих физические наблюдаемые в квантовой механике, дают измеримые значения этих наблюдаемых, в то время как собственные состояния, соответствующие этим собственным значениям, дают возможные состояния, в которых система может находиться при измерении. Измеримые значения энергии квантовой системы задаются собственными значениями оператора Гамильтона, в то время как ее собственные состояния дают возможные энергетические состояния системы. Значение энергии называется вырожденным, если существует по крайней мере два линейно независимых энергетических состояния, связанных с ним. Более того, любая линейная комбинация двух или более вырожденных собственных состояний также является собственным состоянием оператора Гамильтона, соответствующим тому же собственному значению энергии. Это ясно следует из того факта, что собственное пространство собственного значения значения энергии λ является подпространством (будучи ядром гамильтониана минус λ, умноженным на единицу), следовательно, замкнуто относительно линейных комбинаций.

Доказательство приведенной выше теоремы. ^{[2] : стр. 52}

Если представляет собой оператор Гамильтона , а и являются двумя собственными состояниями, соответствующими одному и тому же собственному значению E , то ${\displaystyle {\hat {H}}}$ ${\displaystyle |\psi _{1}\rangle }$ ${\displaystyle |\psi _{2}\rangle }$ $${\displaystyle {\begin{aligned}{\hat {H}}|\psi _{1}\rangle &=E|\psi _{1}\rangle \\{\hat {H}}|\psi _{2}\rangle &=E|\psi _{2}\rangle \end{aligned}}}$$

Пусть , где и — комплексные (в общем случае) константы, будет любой линейной комбинацией и . Тогда, что показывает, что — собственное состояние с тем же собственным значением E . ${\displaystyle |\psi \rangle =c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle }$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle |\psi _{1}\rangle }$ ${\displaystyle |\psi _{2}\rangle }$ $${\displaystyle {\begin{aligned}{\hat {H}}|\psi \rangle &={\hat {H}}(c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle )\\&=c_{1}{\hat {H}}|\psi _{1}\rangle +c_{2}{\hat {H}}|\psi _{2}\rangle \\&=E(c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle )\\&=E|\psi \rangle \end{aligned}}}$$ ${\displaystyle |\psi \rangle }$ ${\displaystyle {\hat {H}}}$

Влияние вырождения на измерение энергии

При отсутствии вырождения, если измеренное значение энергии квантовой системы определено, соответствующее состояние системы предполагается известным, поскольку каждому собственному значению энергии соответствует только одно собственное состояние. Однако, если гамильтониан имеет вырожденное собственное значение степени g _n , то связанные с ним собственные состояния образуют векторное подпространство размерности g _n . В таком случае несколько конечных состояний могут быть, возможно, связаны с одним и тем же результатом , все из которых являются линейными комбинациями ортонормированных собственных векторов g _n . ${\displaystyle {\hat {H}}}$ ${\displaystyle E_{n}}$ ${\displaystyle E_{n}}$ ${\displaystyle |E_{n,i}\rangle }$

В этом случае вероятность того, что значение энергии, измеренное для системы в состоянии, даст значение , определяется суммой вероятностей нахождения системы в каждом из состояний в этом базисе, т.е. ${\displaystyle |\psi \rangle }$ ${\displaystyle E_{n}}$ $${\displaystyle P(E_{n})=\sum _{i=1}^{g_{n}}|\langle E_{n,i}|\psi \rangle |^{2}}$$

Вырождение в разных измерениях

В этом разделе предполагается проиллюстрировать существование вырожденных уровней энергии в квантовых системах, изучаемых в разных измерениях. Изучение одномерных и двумерных систем помогает концептуальному пониманию более сложных систем.

Вырождение в одном измерении

В ряде случаев аналитические результаты можно получить проще при изучении одномерных систем. Для квантовой частицы с волновой функцией , движущейся в одномерном потенциале , независимое от времени уравнение Шредингера можно записать как Поскольку это обыкновенное дифференциальное уравнение, для заданной энергии существует не более двух независимых собственных функций, так что степень вырождения никогда не превышает двух. Можно доказать, что в одном измерении нет вырожденных связанных состояний для нормируемых волновых функций . Достаточным условием на кусочно-непрерывный потенциал и энергию является существование двух действительных чисел с такими, что мы имеем . ^[3] В частности, ограничено снизу в этом критерии. ${\displaystyle |\psi \rangle }$ ${\displaystyle V(x)}$ $${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+V\psi =E\psi }$$ ${\displaystyle E}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle M,x_{0}}$ ${\displaystyle M\neq 0}$ ${\displaystyle \forall x>x_{0}}$ ${\displaystyle V(x)-E\geq M^{2}}$ ${\displaystyle V}$

Вырождение в двумерных квантовых системах

Двумерные квантовые системы существуют во всех трех состояниях материи, и большая часть многообразия, наблюдаемого в трехмерной материи, может быть создана в двух измерениях. Реальные двумерные материалы состоят из моноатомных слоев на поверхности твердых тел. Некоторые примеры двумерных электронных систем, достигнутых экспериментально, включают МОП-транзистор , двумерные сверхрешетки гелия , неона , аргона , ксенона и т. д. и поверхность жидкого гелия . Наличие вырожденных уровней энергии изучается в случаях частицы в ящике и двумерного гармонического осциллятора , которые действуют как полезные математические модели для нескольких систем реального мира.

Частица в прямоугольной плоскости

Рассмотрим свободную частицу в плоскости измерений и в плоскости непроницаемых стенок. Не зависящее от времени уравнение Шредингера для этой системы с волновой функцией можно записать как Допустимые значения энергии равны Нормированная волновая функция равна где ${\displaystyle L_{x}}$ ${\displaystyle L_{y}}$ ${\displaystyle |\psi \rangle }$ $${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{{\partial x}^{2}}}+{\frac {\partial ^{2}\psi }{{\partial y}^{2}}}\right)=E\psi }$$ $${\displaystyle E_{n_{x},n_{y}}={\frac {\pi ^{2}\hbar ^{2}}{2m}}\left({\frac {n_{x}^{2}}{L_{x}^{2}}}+{\frac {n_{y}^{2}}{L_{y}^{2}}}\right)}$$ $${\displaystyle \psi _{n_{x},n_{y}}(x,y)={\frac {2}{\sqrt {L_{x}L_{y}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)}$$ ${\displaystyle n_{x},n_{y}=1,2,3,\dots }$

Итак, квантовые числа и необходимы для описания собственных значений энергии, а наименьшая энергия системы определяется выражением ${\displaystyle n_{x}}$ ${\displaystyle n_{y}}$ $${\displaystyle E_{1,1}=\pi ^{2}{\frac {\hbar ^{2}}{2m}}\left({\frac {1}{L_{x}^{2}}}+{\frac {1}{L_{y}^{2}}}\right)}$$

Для некоторых соизмеримых отношений двух длин и определенные пары состояний вырождены. Если , где p и q — целые числа, состояния и имеют одинаковую энергию и поэтому вырождены друг к другу. ${\displaystyle L_{x}}$ ${\displaystyle L_{y}}$ ${\displaystyle L_{x}/L_{y}=p/q}$ ${\displaystyle (n_{x},n_{y})}$ ${\displaystyle (pn_{y}/q,qn_{x}/p)}$

Частица в квадратном ящике

В этом случае размеры ящика и собственные значения энергии определяются как ${\displaystyle L_{x}=L_{y}=L}$ $${\displaystyle E_{n_{x},n_{y}}={\frac {\pi ^{2}\hbar ^{2}}{2mL^{2}}}(n_{x}^{2}+n_{y}^{2})}$$

Так как и можно менять местами без изменения энергии, каждый уровень энергии имеет вырождение не менее двух, когда и различны. Вырожденные состояния также получаются, когда сумма квадратов квантовых чисел, соответствующих различным уровням энергии, одинакова. Например, три состояния (n _x = 7, n _y = 1), (n _x = 1, n _y = 7) и (n _x = n _y = 5) все имеют и составляют вырожденный набор. ${\displaystyle n_{x}}$ ${\displaystyle n_{y}}$ ${\displaystyle n_{x}}$ ${\displaystyle n_{y}}$ ${\displaystyle E=50{\frac {\pi ^{2}\hbar ^{2}}{2mL^{2}}}}$

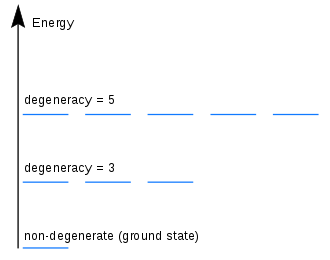
Степени вырождения различных уровней энергии для частицы в квадратном ящике:

Частица в кубическом ящике

В этом случае размеры ящика и собственные значения энергии зависят от трех квантовых чисел. ${\displaystyle L_{x}=L_{y}=L_{z}=L}$ $${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\pi ^{2}\hbar ^{2}}{2mL^{2}}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})}$$

Поскольку и можно менять местами без изменения энергии, каждый уровень энергии имеет вырождение не менее трех, когда три квантовых числа не все равны . ${\displaystyle n_{x}}$ ${\displaystyle n_{y}}$ ${\displaystyle n_{z}}$

Нахождение единственного собственного базиса в случае вырождения

Если два оператора и коммутируют, т.е. , то для каждого собственного вектора , есть также собственный вектор с тем же собственным значением. Однако, если это собственное значение, скажем , вырождено, можно сказать, что принадлежит собственному пространству , которое называется глобально инвариантным относительно действия . ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle [{\hat {A}},{\hat {B}}]=0}$ ${\displaystyle |\psi \rangle }$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}|\psi \rangle }$ ${\displaystyle {\hat {A}}}$ ${\displaystyle \lambda }$ ${\displaystyle {\hat {B}}|\psi \rangle }$ ${\displaystyle E_{\lambda }}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$

Для двух коммутирующих наблюдаемых A и B можно построить ортонормированный базис пространства состояний с собственными векторами, общими для двух операторов. Однако, является вырожденным собственным значением , тогда это собственное подпространство , которое инвариантно относительно действия , поэтому представление в собственном базисе является не диагональной, а блочно-диагональной матрицей , т.е. вырожденные собственные векторы не являются, вообще говоря, собственными векторами . Однако, всегда можно выбрать в каждом вырожденном собственном подпространстве базис из собственных векторов, общих для и . ${\displaystyle \lambda }$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$

Выбор полного набора наблюдаемых объектов для поездок на работу

Если заданная наблюдаемая A невырождена, то существует уникальный базис, образованный ее собственными векторами. С другой стороны, если одно или несколько собственных значений вырождены, указания собственного значения недостаточно для характеристики базисного вектора. Если, выбрав наблюдаемую , которая коммутирует с , можно построить ортонормированный базис собственных векторов, общих для и , который является уникальным для каждой из возможных пар собственных значений {a,b}, то говорят, что и образуют полный набор коммутирующих наблюдаемых . Однако, если уникальный набор собственных векторов все еще не может быть указан, по крайней мере для одной из пар собственных значений, третья наблюдаемая , которая коммутирует с обоими и может быть найдена таким образом, что эти три образуют полный набор коммутирующих наблюдаемых. ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$ ${\displaystyle {\hat {C}}}$ ${\displaystyle {\hat {A}}}$ ${\displaystyle {\hat {B}}}$

Из этого следует, что собственные функции гамильтониана квантовой системы с общим значением энергии должны быть помечены путем предоставления некоторой дополнительной информации, что может быть сделано путем выбора оператора, который коммутирует с гамильтонианом. Эти дополнительные метки требуют именования уникальной собственной функции энергии и обычно связаны с константами движения системы.

Вырожденные энергетические собственные состояния и оператор четности

Оператор четности определяется его действием в представлении изменения r на −r, т. е. Можно показать, что собственные значения P ограничены , которые оба являются вырожденными собственными значениями в бесконечномерном пространстве состояний. Собственный вектор P с собственным значением +1 называется четным, а с собственным значением −1 — нечетным. ${\displaystyle |r\rangle }$ $${\displaystyle \langle r|P|\psi \rangle =\psi (-r)}$$ ${\displaystyle \pm 1}$

Теперь четный оператор — это тот, который удовлетворяет , в то время как нечетный оператор — это тот, который удовлетворяет Поскольку квадрат оператора импульса четный, если потенциал V(r) четный, то говорят, что гамильтониан является четным оператором. В этом случае, если каждое из его собственных значений невырождено, каждый собственный вектор обязательно является собственным состоянием P, и, следовательно, можно искать собственные состояния среди четных и нечетных состояний. Однако, если одно из собственных состояний энергии не имеет определенной четности , можно утверждать, что соответствующее собственное значение вырождено и является собственным вектором с тем же собственным значением, что и . ${\displaystyle {\hat {A}}}$ $${\displaystyle {\tilde {A}}=P{\hat {A}}P}$$ $${\displaystyle [P,{\hat {A}}]=0}$$ ${\displaystyle {\hat {B}}}$ $${\displaystyle P{\hat {B}}+{\hat {B}}P=0}$$ ${\displaystyle {\hat {p}}^{2}}$ ${\displaystyle {\hat {H}}}$ ${\displaystyle {\hat {H}}}$ ${\displaystyle P|\psi \rangle }$ ${\displaystyle {\hat {H}}}$ ${\displaystyle |\psi \rangle }$

Вырождение и симметрия

Физическим источником вырождения в квантово-механической системе часто является наличие некоторой симметрии в системе. Изучение симметрии квантовой системы может, в некоторых случаях, позволить нам найти уровни энергии и вырождения без решения уравнения Шредингера, тем самым уменьшая усилия.

Математически связь вырождения с симметрией можно прояснить следующим образом. Рассмотрим операцию симметрии, связанную с унитарным оператором S . При такой операции новый гамильтониан связан с исходным гамильтонианом преобразованием подобия , генерируемым оператором S , таким образом, что , поскольку S является унитарным. Если гамильтониан остается неизменным при операции преобразования S , мы имеем Теперь, если является собственным энергетическим состоянием, где E является соответствующим собственным значением энергии. что означает, что является также собственным энергетическим состоянием с тем же собственным значением E . Если два состояния и линейно независимы (т. е. физически различны), они, следовательно, вырождены. ${\displaystyle H'=SHS^{-1}=SHS^{\dagger }}$ $${\displaystyle {\begin{aligned}SHS^{\dagger }&=H\\[1ex]SHS^{-1}&=H\\[1ex]SH&=HS\\[1ex][S,H]&=0\end{aligned}}}$$ ${\displaystyle |\alpha \rangle }$ $${\displaystyle H|\alpha \rangle =E|\alpha \rangle }$$ $${\displaystyle HS|\alpha \rangle =SH|\alpha \rangle =SE|\alpha \rangle =ES|\alpha \rangle }$$ ${\displaystyle S|\alpha \rangle }$ ${\displaystyle |\alpha \rangle }$ ${\displaystyle S|\alpha \rangle }$

В случаях, когда S характеризуется непрерывным параметром , все состояния формы имеют одинаковое собственное значение энергии. ${\displaystyle \epsilon }$ ${\displaystyle S(\epsilon )|\alpha \rangle }$

Группа симметрии гамильтониана

Говорят, что набор всех операторов, коммутирующих с гамильтонианом квантовой системы, образует группу симметрии гамильтониана. Коммутаторы генераторов этой группы определяют алгебру группы. N-мерное представление группы симметрии сохраняет таблицу умножения операторов симметрии. Возможные вырождения гамильтониана с конкретной группой симметрии задаются размерностями неприводимых представлений группы. Собственные функции , соответствующие n-кратно вырожденному собственному значению, образуют базис для n-мерного неприводимого представления группы симметрии гамильтониана.

Виды вырождения

Вырождения в квантовой системе могут иметь систематический или случайный характер.

Систематическая или существенная дегенерация

Это также называется геометрическим или нормальным вырождением и возникает из-за наличия в рассматриваемой системе некоторого вида симметрии, т. е. инвариантности гамильтониана относительно определенной операции, как описано выше. Представление, полученное из нормального вырождения, неприводимо, и соответствующие собственные функции образуют основу этого представления.

Случайное вырождение

Это тип вырождения, возникающий из-за некоторых особенностей системы или функциональной формы рассматриваемого потенциала, и, возможно, связанный со скрытой динамической симметрией в системе. ^[4] Это также приводит к сохраняющимся величинам, которые часто нелегко идентифицировать. Случайные симметрии приводят к этим дополнительным вырождениям в дискретном энергетическом спектре. Случайное вырождение может быть вызвано тем, что группа гамильтониана не является полной. Эти вырождения связаны с существованием связанных орбит в классической физике.

Примеры: потенциалы Кулона и гармонического осциллятора.

Для частицы в центральном потенциале 1/ r вектор Лапласа–Рунге–Ленца является сохраняющейся величиной, возникающей в результате случайного вырождения, в дополнение к сохранению углового момента из -за вращательной инвариантности.

Для частицы, движущейся по конусу под действием потенциалов 1/ r и r ² с центром на вершине конуса, сохраняющиеся величины, соответствующие случайной симметрии, будут представлять собой две компоненты эквивалента вектора Рунге-Ленца, в дополнение к одной компоненте вектора углового момента. Эти величины порождают симметрию SU(2) для обоих потенциалов.

Пример: Частица в постоянном магнитном поле.

Частица, движущаяся под действием постоянного магнитного поля, совершающая циклотронное движение по круговой орбите, является еще одним важным примером случайной симметрии. Мультиплеты симметрии в этом случае являются уровнями Ландау , которые бесконечно вырождены.

Примеры

Атом водорода

В атомной физике связанные состояния электрона в атоме водорода показывают нам полезные примеры вырождения. В этом случае гамильтониан коммутирует с полным орбитальным угловым моментом , его компонентой вдоль z-направления, , полным спиновым угловым моментом и его z-компонентой . Квантовые числа, соответствующие этим операторам, равны , , (всегда 1/2 для электрона) и соответственно. ${\displaystyle {\hat {L}}^{2}}$ ${\displaystyle {\hat {L}}_{z}}$ ${\displaystyle {\hat {S}}^{2}}$ ${\displaystyle {\hat {S}}_{z}}$ ${\displaystyle \ell }$ ${\displaystyle m_{\ell }}$ ${\displaystyle s}$ ${\displaystyle m_{s}}$

Уровни энергии в атоме водорода зависят только от главного квантового числа n . Для заданного n все состояния, соответствующие , имеют одинаковую энергию и вырождены. Аналогично для заданных значений n и ℓ , состояния с вырождены. Степень вырождения уровня энергии E _n , следовательно, удваивается, если включить вырождение спина. ^{[1] : 267f} ${\displaystyle \ell =0,\ldots ,n-1}$ ${\displaystyle (2\ell +1)}$ ${\displaystyle m_{\ell }=-\ell ,\ldots ,\ell }$ $${\displaystyle \sum _{\ell \mathop {=} 0}^{n-1}(2\ell +1)=n^{2},}$$

Вырождение относительно является существенным вырождением, которое присутствует для любого центрального потенциала и возникает из-за отсутствия предпочтительного пространственного направления. Вырождение относительно часто описывается как случайное вырождение, но его можно объяснить в терминах специальных симметрий уравнения Шредингера, которые справедливы только для атома водорода, в котором потенциальная энергия задается законом Кулона . ^{[1] : 267f} ${\displaystyle m_{\ell }}$ ${\displaystyle \ell }$

Изотропный трехмерный гармонический осциллятор

Это бесспиновая частица массы m, движущаяся в трехмерном пространстве , подверженная центральной силе , абсолютная величина которой пропорциональна расстоянию частицы от центра силы. Она называется изотропной, поскольку действующий на нее потенциал инвариантен относительно вращения, т. е. где — угловая частота, заданная выражением . $${\displaystyle F=-kr}$$ ${\displaystyle V(r)}$ $${\displaystyle V(r)={\tfrac {1}{2}}m\omega ^{2}r^{2}}$$ ${\displaystyle \omega }$ ${\textstyle {\sqrt {k/m}}}$

Поскольку пространство состояний такой частицы является тензорным произведением пространств состояний, связанных с отдельными одномерными волновыми функциями, то не зависящее от времени уравнение Шредингера для такой системы задается следующим образом: $${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\right)+{\frac {1}{2}}{m\omega ^{2}\left(x^{2}+y^{2}+z^{2}\right)\psi }=E\psi }$$

Итак, собственные значения энергии равны или, где n — неотрицательное целое число. Итак, уровни энергии вырождены, а степень вырождения равна числу различных наборов, удовлетворяющих Вырождение -го состояния можно найти, рассмотрев распределение квантов по , и . Наличие 0 в дает возможности для распределения по и . Наличие 1 кванта в дает возможности по и и так далее. Это приводит к общему результату и суммирование по всем приводит к вырождению -го состояния, Для основного состояния вырождение равно , поэтому состояние невырождено. Для всех более высоких состояний вырождение больше 1, поэтому состояние вырождено. $${\displaystyle E_{n_{x},n_{y},n_{z}}=\left(n_{x}+n_{y}+n_{z}+{\tfrac {3}{2}}\right)\hbar \omega }$$ $${\displaystyle E_{n}=\left(n+{\tfrac {3}{2}}\right)\hbar \omega }$$ ${\displaystyle \{n_{x},n_{y},n_{z}\}}$ $${\displaystyle n_{x}+n_{y}+n_{z}=n}$$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n_{x}}$ ${\displaystyle n_{y}}$ ${\displaystyle n_{z}}$ ${\displaystyle n_{x}}$ ${\displaystyle n+1}$ ${\displaystyle n_{y}}$ ${\displaystyle n_{z}}$ ${\displaystyle n_{x}}$ ${\displaystyle n}$ ${\displaystyle n_{y}}$ ${\displaystyle n_{z}}$ ${\displaystyle n-n_{x}+1}$ ${\displaystyle n}$ ${\displaystyle n}$ $${\displaystyle \sum _{n_{x}=0}^{n}(n-n_{x}+1)={\frac {(n+1)(n+2)}{2}}}$$ ${\displaystyle n=0}$ ${\displaystyle 1}$

Устранение вырождения

Вырождение в квантово-механической системе может быть устранено, если базовая симметрия нарушается внешним возмущением . Это вызывает расщепление вырожденных уровней энергии. По сути, это расщепление исходных неприводимых представлений на более низкоразмерные представления возмущенной системы.

Математически расщепление из-за приложения малого потенциала возмущения можно вычислить с помощью независимой от времени вырожденной теории возмущений . Это схема приближения, которая может быть применена для нахождения решения уравнения собственных значений для гамильтониана H квантовой системы с приложенным возмущением, учитывая решение для гамильтониана H ₀ для невозмущенной системы. Она включает в себя разложение собственных значений и собственных элементов гамильтониана H в ряд возмущений. Вырожденные собственные состояния с заданным собственным значением энергии образуют векторное подпространство, но не каждый базис собственных состояний этого пространства является хорошей отправной точкой для теории возмущений, поскольку обычно рядом с ними не будет никаких собственных состояний возмущенной системы. Правильным выбором базиса является тот, который диагонализирует гамильтониан возмущения в вырожденном подпространстве.

Физические примеры снятия вырождения возмущением

Ниже приведены некоторые важные примеры физических ситуаций, в которых вырожденные уровни энергии квантовой системы расщепляются при приложении внешнего возмущения.

Нарушение симметрии в двухуровневых системах

Двухуровневая система по сути относится к физической системе, имеющей два состояния, энергии которых близки друг к другу и сильно отличаются от энергий других состояний системы. Все вычисления для такой системы выполняются в двумерном подпространстве пространства состояний.

Если основное состояние физической системы дважды вырождено, любая связь между двумя соответствующими состояниями понижает энергию основного состояния системы и делает ее более стабильной.

Если и являются уровнями энергии системы, такими, что , и возмущение представлено в двумерном подпространстве в виде следующей матрицы 2×2 , то возмущенные энергии равны ${\displaystyle E_{1}}$ ${\displaystyle E_{2}}$ ${\displaystyle E_{1}=E_{2}=E}$ ${\displaystyle W}$ $${\displaystyle \mathbf {W} ={\begin{bmatrix}0&W_{12}\\[1ex]W_{12}^{*}&0\end{bmatrix}}.}$$ $${\displaystyle {\begin{aligned}E_{+}&=E+|W_{12}|\\E_{-}&=E-|W_{12}|\end{aligned}}}$$

Примерами двухуровневых систем, в которых вырождение энергетических состояний нарушается наличием недиагональных членов в гамильтониане, возникающих в результате внутреннего взаимодействия из-за внутреннего свойства системы, являются:

• Бензол с двумя возможными расположениями трех двойных связей между соседними атомами углерода .
• Молекула аммиака , в которой атом азота может находиться как выше, так и ниже плоскости, определяемой тремя атомами водорода .
• ЧАС⁺
  ₂молекула, в которой электрон может быть локализован вокруг любого из двух ядер.

Расщепление тонкой структуры

Поправки к кулоновскому взаимодействию между электроном и протоном в атоме водорода, обусловленные релятивистским движением и спин-орбитальной связью, приводят к снятию вырождения уровней энергии для различных значений l, соответствующих одному главному квантовому числу n .

Гамильтониан возмущения, обусловленный релятивистской поправкой, определяется как , где — оператор импульса, а — масса электрона. Релятивистская поправка к энергии первого порядка в базисе определяется как $${\displaystyle H_{r}=-p^{4}/8m^{3}c^{2}}$$ ${\displaystyle p}$ ${\displaystyle m}$ ${\displaystyle |nlm\rangle }$ $${\displaystyle E_{r}=\left(-1/8m^{3}c^{2}\right)\left\langle n\ell m\right|p^{4}\left|n\ell m\right\rangle }$$

Где находится постоянная тонкой структуры ? ${\displaystyle p^{4}=4m^{2}(H^{0}+e^{2}/r)^{2}}$ $${\displaystyle {\begin{aligned}E_{r}&=-{\frac {1}{2mc^{2}}}\left[E_{n}^{2}+2E_{n}e^{2}\left\langle {\frac {1}{r}}\right\rangle +e^{4}\left\langle {\frac {1}{r^{2}}}\right\rangle \right]\\&=-{\frac {1}{2}}mc^{2}\alpha ^{4}\left[-3/(4n^{4})+1/{n^{3}(\ell +1/2)}\right]\end{aligned}}}$$ ${\displaystyle \alpha }$

Спин-орбитальное взаимодействие относится к взаимодействию между собственным магнитным моментом электрона и магнитным полем, испытываемым им из-за относительного движения с протоном. Гамильтониан взаимодействия есть что может быть записано как $${\displaystyle H_{so}=-{\frac {e}{mc}}{\frac {\mathbf {m} \cdot \mathbf {L} }{r^{3}}}={\frac {e^{2}}{m^{2}c^{2}r^{3}}}\mathbf {S} \cdot \mathbf {L} }$$ $${\displaystyle H_{so}={\frac {e^{2}}{4m^{2}c^{2}r^{3}}}\left[J^{2}-L^{2}-S^{2}\right]}$$

Поправка к энергии первого порядка в базисе, где гамильтониан возмущения диагонален, определяется выражением , где — радиус Бора . Полный сдвиг энергии тонкой структуры определяется выражением для . ${\displaystyle |j,m,\ell ,1/2\rangle }$ $${\displaystyle E_{so}={\frac {\hbar ^{2}e^{2}}{4m^{2}c^{2}}}{\frac {j(j+1)-\ell (\ell +1)-{\frac {3}{4}}}{a_{0}^{3}n^{3}\ell (\ell +{\frac {1}{2}})(\ell +1)}}}$$ ${\displaystyle a_{0}}$ $${\displaystyle E_{fs}=-{\frac {mc^{2}\alpha ^{4}}{2n^{3}}}\left[1/(j+1/2)-3/4n\right]}$$ ${\textstyle j=\ell \pm {\tfrac {1}{2}}}$

эффект Зеемана

Расщепление энергетических уровней атома при помещении его во внешнее магнитное поле из-за взаимодействия магнитного момента атома с приложенным полем известно как эффект Зеемана . ${\displaystyle {\vec {m}}}$

Принимая во внимание орбитальный и спиновый угловые моменты, и , соответственно, одного электрона в атоме водорода, гамильтониан возмущения задается выражением где и . Таким образом, Теперь, в случае слабополевого эффекта Зеемана, когда приложенное поле слабо по сравнению с внутренним полем, спин-орбитальная связь доминирует и и не сохраняются по отдельности. Хорошие квантовые числа - это n , ℓ , j и m _j , и в этом базисе можно показать, что поправка к энергии первого порядка задается выражением где называется магнетоном Бора . Таким образом, в зависимости от значения каждый вырожденный энергетический уровень расщепляется на несколько уровней. ${\displaystyle \mathbf {L} }$ ${\displaystyle \mathbf {S} }$ $${\displaystyle {\hat {V}}=-(\mathbf {m} _{\ell }+\mathbf {m} _{s})\cdot \mathbf {B} }$$ ${\displaystyle \mathbf {m} _{\ell }=-e\mathbf {L} /2m}$ ${\displaystyle \mathbf {m} _{s}=-e\mathbf {S} /m}$ $${\displaystyle {\hat {V}}={\frac {e}{2m}}(\mathbf {L} +2\mathbf {S} )\cdot \mathbf {B} }$$ ${\textstyle \mathbf {L} }$ ${\textstyle \mathbf {S} }$ $${\displaystyle E_{z}=-\mu _{B}g_{j}Bm_{j},}$$ ${\displaystyle \mu _{B}={e\hbar }/2m}$ ${\displaystyle m_{j}}$

Снятие вырождения внешним магнитным полем

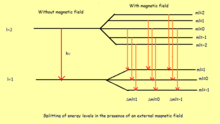
В случае эффекта Зеемана с сильным полем, когда приложенное поле достаточно сильное, так что орбитальный и спиновый угловые моменты разделяются, хорошими квантовыми числами теперь являются n , l , m _l и m _s . Здесь L _z и S _z сохраняются, поэтому гамильтониан возмущения задается предположением, что магнитное поле направлено вдоль z -направления. Таким образом, для каждого значения m _ℓ существует два возможных значения m _s , . $${\displaystyle {\hat {V}}=eB(L_{z}+2S_{z})/2m}$$ $${\displaystyle {\hat {V}}=eB(m_{\ell }+2m_{s})/2m}$$ ${\displaystyle \pm 1/2}$

Эффект Старка

Расщепление энергетических уровней атома или молекулы под воздействием внешнего электрического поля известно как эффект Штарка .

Для атома водорода гамильтониан возмущения имеет вид, если электрическое поле выбрано вдоль направления z . $${\displaystyle {\hat {H}}_{s}=-|e|Ez}$$

Поправки к энергии, обусловленные приложенным полем, задаются ожидаемым значением в базисе. С помощью правил отбора можно показать, что когда и . ${\displaystyle {\hat {H}}_{s}}$ ${\displaystyle |n\ell m\rangle }$ ${\displaystyle \langle n\ell m_{\ell }|z|n_{1}\ell _{1}m_{\ell 1}\rangle \neq 0}$ ${\displaystyle \ell =\ell _{1}\pm 1}$ ${\displaystyle m_{\ell }=m_{\ell 1}}$

Вырождение снимается только для определенных состояний, подчиняющихся правилам отбора, в первом порядке. Расщепление первого порядка в уровнях энергии для вырожденных состояний и , оба соответствующих n = 2, задается выражением . ${\displaystyle |2,0,0\rangle }$ ${\displaystyle |2,1,0\rangle }$ ${\displaystyle \Delta E_{2,1,m_{\ell }}=\pm |e|\hbar ^{2}/(m_{e}e^{2})E}$

Смотрите также

• Плотность состояний

Ссылки

1. Merzbacher, Eugen (1998). Квантовая механика (3-е изд.). Нью-Йорк: John Wiley. ISBN 0-471-88702-1.
2. Левин, Айра Н. (1991). Квантовая химия (4-е изд.). Prentice Hall. стр. 52. ISBN 0-205-12770-3.
3. Messiah, Albert (1967). Квантовая механика (3-е изд.). Amsterdam, NLD: North-Holland. стр. 98–106. ISBN 0-471-88702-1.
4. Макинтош, Гарольд В. (1959). «О случайном вырождении в классической и квантовой механике» (PDF) . Американский журнал физики . 27 (9). Американская ассоциация учителей физики (AAPT): 620–625. Bibcode : 1959AmJPh..27..620M. doi : 10.1119/1.1934944. ISSN  0002-9505.

Дальнейшее чтение

• Коэн-Таннуджи, Клод; Диу, Бернар; Лалоэ, Франк. Квантовая механика. Том. 1. Германн. ISBN 978-2-7056-8392-4.^{[ необходима полная цитата ]}
• Шанкар, Рамамурти (2013). Принципы квантовой механики. Springer. ISBN 978-1-4615-7675-4.^{[ необходима полная цитата ]}
• Ларсон, Рон ; Фальво, Дэвид К. (30 марта 2009 г.). Элементарная линейная алгебра, расширенное издание. Cengage Learning. стр. 8–. ISBN 978-1-305-17240-1.
• Хобсон; Райли (27 августа 2004 г.). Математические методы в физике и инженерии (Clpe) 2-е изд. Cambridge University Press. ISBN 978-0-521-61296-8.
• Хеммер (2005). Квантемеканикк: ПК Хеммер. Тапир академиск форлаг. Тиллегг 3: дополнение к разделам 3.1, 3.3 и 3.5. ISBN 978-82-519-2028-5.
• Квантовое вырождение в двумерных системах, Дебнараян Джана, кафедра физики, Университетский колледж науки и технологий
• Аль-Хашими, Мунир (2008). Случайная симметрия в квантовой физике.