Порог ошибки (эволюция)

Теоретический предел скорости мутаций

В эволюционной биологии и популяционной генетике порог ошибки ( или критическая частота мутаций ) представляет собой ограничение на количество пар оснований, которые может иметь самовоспроизводящаяся молекула, прежде чем мутация уничтожит информацию в последующих поколениях молекулы. Порог ошибки имеет решающее значение для понимания «парадокса Эйгена».

Порог ошибки — это концепция происхождения жизни ( абиогенеза ), в частности, очень ранней жизни, до появления ДНК . Предполагается , что первыми самовоспроизводящимися молекулами могли быть небольшие рибозимоподобные молекулы РНК . Эти молекулы состоят из цепочек пар оснований или «цифр», и их порядок представляет собой код, который определяет, как молекула взаимодействует с окружающей средой. Любая репликация подвержена мутационной ошибке. Во время процесса репликации каждая цифра имеет определенную вероятность быть заменена какой-либо другой цифрой, что меняет способ взаимодействия молекулы с окружающей средой и может увеличивать или уменьшать ее приспособленность или способность к воспроизведению в этой среде.

Фитнес-ландшафт

Манфред Эйген в своей статье 1971 года отметил (Eigen 1971), что этот процесс мутации накладывает ограничение на количество цифр, которое может иметь молекула. Если молекула превышает этот критический размер, эффект мутаций становится подавляющим, и неконтролируемый процесс мутации уничтожит информацию в последующих поколениях молекулы. Порог ошибки также контролируется «приспособленностью» молекул. Ландшафт фитнеса характеризуется двумя понятиями: ростом (= приспособленность) и расстоянием (= количество мутаций). Подобные молекулы «близки» друг к другу, а молекулы, которые более приспособлены, чем другие, и с большей вероятностью воспроизводятся, находятся «выше» в ландшафте.

Если конкретная последовательность и ее соседи имеют высокую приспособленность, они образуют квазивид и смогут поддерживать более длинные длины последовательности, чем подходящая последовательность с небольшим количеством подходящих соседей или менее подходящая окрестность последовательностей. Кроме того, Уилке (Wilke 2005) отметил, что концепция порога ошибки не применяется в тех частях ландшафта, где есть летальные мутации, в которых индуцированная мутация приводит к нулевой приспособленности и запрещает молекуле воспроизводиться.

Парадокс Эйгена

Парадокс Эйгена — одна из самых неразрешимых загадок в изучении происхождения жизни. Считается, что описанная выше концепция порога ошибки ограничивает размер самовоспроизводящихся молекул, возможно, несколькими сотнями цифр, однако почти вся жизнь на Земле требует гораздо более длинных молекул для кодирования своей генетической информации. В живых клетках эту проблему решают ферменты, которые восстанавливают мутации, позволяя кодирующим молекулам достигать размеров порядка миллионов пар оснований. Эти большие молекулы, конечно, должны кодировать те самые ферменты, которые их восстанавливают, и в этом заключается парадокс Эйгена, впервые сформулированный Манфредом Эйгеном в его статье 1971 года (Eigen 1971). ^[1] Проще говоря, парадокс Эйгена сводится к следующему:

• Без ферментов исправления ошибок максимальный размер реплицирующейся молекулы составляет около 100 пар оснований.
• Чтобы реплицирующаяся молекула могла кодировать ферменты исправления ошибок, она должна быть существенно больше 100 оснований.

Это парадокс типа «курица или яйцо» , но с еще более трудным решением. Что появилось раньше: большой геном или ферменты, исправляющие ошибки? Был предложен ряд решений этого парадокса:

• Модель стохастического корректора (Сатмари и Мейнард Смит, 1995). В этом предложенном решении несколько примитивных молекул, скажем, двух разных типов, каким-то образом связаны друг с другом, возможно, с помощью капсулы или «клеточной стенки». Если их репродуктивный успех усиливается, скажем, за счет равного количества молекул в каждой клетке, а размножение происходит путем деления, при котором каждый из различных типов молекул случайным образом распределяется среди «детей», то процесс отбора будет способствовать такому равному представительству в клетках. клетках, даже если одна из молекул может иметь селективное преимущество перед другой.
• Ослабленный порог ошибки (Kun et al., 2005). Исследования реальных рибозимов показывают, что частота мутаций может быть существенно меньше, чем ожидалось вначале, - порядка 0,001 на пару оснований за репликацию. Это может обеспечить длину последовательности порядка 7-8 тысяч пар оснований, достаточную для включения элементарных ферментов коррекции ошибок.

Простая математическая модель

Рассмотрим трехзначную молекулу [A,B,C], где A, B и C могут принимать значения 0 и 1. Таких последовательностей восемь ([000], [001], [010], [011] , [100], [101], [110] и [111]). Предположим, что молекула [000] является наиболее подходящей; при каждой репликации он производит среднее количество копий, где . Эта молекула называется «главной последовательностью». Остальные семь последовательностей менее подходят; каждый из них производит только 1 копию за репликацию. Репликация каждой из трех цифр осуществляется со скоростью мутации μ. Другими словами, при каждом повторении цифры последовательности существует вероятность того, что она окажется ошибочной; 0 будет заменен на 1 или наоборот. Давайте проигнорируем двойные мутации и гибель молекул (популяция будет расти бесконечно) и разделим восемь молекул на три класса в зависимости от их расстояния Хэмминга от мастер-последовательности: ${\displaystyle a}$ ${\displaystyle a>1}$ ${\displaystyle \mu }$

Обратите внимание, что количество последовательностей для расстояния d — это просто биномиальный коэффициент для L=3, и что каждую последовательность можно представить как вершину трехмерного куба L=3, причем каждое ребро куба определяет путь мутации, в котором Изменение расстояния Хэмминга равно нулю или ±1. Видно, что, например, одна треть мутаций молекул [001] приведет к образованию молекул [000], а остальные две трети дадут молекулы класса 2 [011] и [101]. Теперь мы можем записать выражение для дочерних популяций класса i через родительские популяции . ${\displaystyle {\tbinom {L}{d}}}$ ${\displaystyle n'_{i}}$ ${\displaystyle n_{j}}$

${\displaystyle n'_{i}=\sum _{j=0}^{3}w_{ij}n_{j}}$

где матрица ' w ', включающая естественный отбор и мутацию, согласно квазивидовой модели , определяется выражением:

${\displaystyle \mathbf {w} ={\begin{bmatrix}a\cdot Q&3a\cdot \mu &0&0\\\mu &Q&2\mu &0\\0&2\mu &Q&\mu \\0&0&3\mu &Q\end{bmatrix}}}$

где вероятность того, что вся молекула будет успешно реплицирована. Собственные векторы матрицы w дадут равновесную численность населения для каждого класса. Например, если скорость мутаций µ равна нулю, у нас будет Q=1, а равновесные концентрации будут . Мастер-последовательность, будучи наиболее приспособленной, останется единственной, кто выживет. Если у нас точность репликации Q = 0,95 и генетическое преимущество a = 1,05, то равновесные концентрации будут примерно . Видно, что основная последовательность не является такой доминирующей; тем не менее, последовательности с низким расстоянием Хэмминга составляют большинство. Если точность репликации Q приближается к 0, то равновесные концентрации будут примерно равны . Это популяция с равным количеством каждой из 8 последовательностей. (Если бы у нас была совершенно равная популяция всех последовательностей, у нас была бы популяция [1,3,3,1]/8.) ${\displaystyle Q=(1-\mu )^{L}}$ ${\displaystyle [n_{0},n_{1},n_{2},n_{3}]=[1,0,0,0]}$ ${\displaystyle [0.33,0.38,0.24,0.06]}$ ${\displaystyle [0.125,0.375,0.375,0.125]}$

Если мы теперь перейдем к случаю, когда количество пар оснований велико, скажем, L=100, мы получим поведение, напоминающее фазовый переход . График ниже слева показывает ряд равновесных концентраций, разделенных на биномиальный коэффициент . (Это умножение покажет популяцию для отдельной последовательности на этом расстоянии и даст плоскую линию для равного распределения.) Селективное преимущество основной последовательности установлено на уровне a=1,05. Горизонтальная ось — расстояние Хэмминга d  . Различные кривые соответствуют разным общим скоростям мутаций . Видно, что при низких значениях суммарной частоты мутаций популяция состоит из квазивидов , собравшихся вблизи мастер-последовательности. При общей частоте мутаций около 1-Q=0,05 распределение быстро распространяется и равномерно заполняет все последовательности. График ниже справа показывает дробную популяцию мастер-последовательности как функцию общей частоты мутаций. Опять же видно, что ниже критической скорости мутаций около 1-Q=0,05 главная последовательность содержит большую часть популяции, тогда как выше этой скорости она содержит только около общей популяции. ${\displaystyle {\tbinom {100}{k}}}$ ${\displaystyle (1-Q)}$ ${\displaystyle 2^{-L}\approx 10^{-30}}$

Численность популяции как функция расстояния Хэмминга d и скорости мутаций (1-Q). Горизонтальная ось d   представляет собой расстояние Хэмминга молекулярных последовательностей от мастер-последовательности. Вертикальная ось представляет собой логарифм численности населения для любой последовательности на этом расстоянии, разделенный на общую численность населения (таким образом, деление n _d на биномиальный коэффициент). Общее количество цифр в последовательности равно L=100, а главная последовательность имеет селективное преимущество a=1,05.

Популяция основной последовательности как доля от общей популяции ( n ) как функция общей частоты мутаций (1-Q). Общее количество цифр в последовательности равно L=100, а главная последовательность имеет селективное преимущество a=1,05. Видно, что «фазовый переход» происходит примерно при 1-Q=0,05.

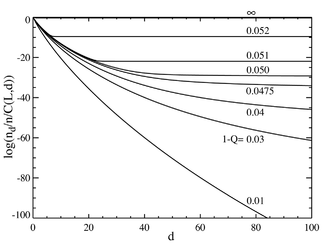
Видно, что наблюдается резкий переход при значении 1-Q   чуть больше 0,05. При частоте мутаций выше этого значения популяция мастер-последовательности падает практически до нуля. Выше этого значения он доминирует.

В пределе, когда L приближается к бесконечности, система действительно имеет фазовый переход при критическом значении Q: . Можно было бы думать об общей частоте мутаций (1-Q) как о своего рода «температуре», которая «плавит» точность молекулярных последовательностей выше критической «температуры» . Чтобы произошла достоверная репликация, информация должна быть «заморожена» в геноме. ${\displaystyle Q_{c}=1/a.}$ ${\displaystyle 1-Q_{c}}$

Смотрите также

• Ошибка катастрофы
• Вихрь вымирания
• Генетическая энтропия
• Генетическая эрозия
• трещотка Мюллера

Рекомендации

1. Холмс, Эдвард К. (2009). Эволюция и появление РНК-вирусов. Издательство Оксфордского университета. стр. 22, 23, 48. ISBN. 9780199211128. Проверено 1 февраля 2019 г.

• Эйген, М. (1971). «Самоорганизация материи и эволюция биологических макромолекул». Naturwissenschaften . 58 (10): 465–523. Бибкод : 1971NW.....58..465E. дои : 10.1007/BF00623322. PMID  4942363. S2CID  38296619.
• «Теория квазивидов в контексте популяционной генетики - Клаус О. Уилк» (PDF) . Проверено 12 октября 2005 г.
• Кампос, PRA; Фонтанари, Дж. Ф. (1999). «Масштабирование конечного размера перехода порога ошибки в конечных популяциях» (PDF) . Дж. Физ. А: Математика. Ген . 32 (1): Л1–Л7. arXiv : cond-mat/9809209 . Бибкод : 1999JPhA...32L...1C. дои : 10.1088/0305-4470/32/1/001. S2CID  16500591.
• Холмс, Эдвард К. (2005). «О том, чтобы быть правильным размером». Природная генетика . 37 (9): 923–924. дои : 10.1038/ng0905-923. ПМК  7097767 . ПМИД  16132047.
• Эорс Сатмари; Джон Мейнард Смит (1995). «Основные эволюционные переходы». Природа . 374 (6519): 227–232. Бибкод : 1995Natur.374..227S. дои : 10.1038/374227a0. PMID  7885442. S2CID  4315120.
• Луис Вильярреал; Гюнтер Вицани (2013). «Переосмысление теории квазивидов: от наиболее приспособленного типа к кооперативным консорциумам». Всемирный журнал биологической химии . 4 (4): 79–90. дои : 10.4331/wjbc.v4.i4.79 . ПМК  3856310 . ПМИД  24340131.
• Адам Кун; Мауро Сантос; Эёрс Сатмари (2005). «Настоящие рибозимы предполагают сниженный порог ошибки». Природная генетика . 37 (9): 1008–1011. дои : 10.1038/ng1621. PMID  16127452. S2CID  30582475.