Блокировка карданного подвеса

Самолет с запертым подвесом. Когда подвесы тангажа (зеленый) и рыскания (пурпурный) выравниваются, изменения крена (синий) и рыскания применяют то же вращение к самолету.

Блокировка карданного подвеса — это потеря одной степени свободы в многомерном механизме при определенных выравниваниях осей. В трехмерном трехкарданном механизме блокировка карданного подвеса происходит, когда оси двух карданных подвесов приводятся в параллельную конфигурацию, «запирая» систему во вращении в вырожденном двумерном пространстве.

Термин gimball- lock может вводить в заблуждение в том смысле, что ни один из отдельных карданных шарниров на самом деле не ограничен. Все три карданных шарнира могут свободно вращаться вокруг своих соответствующих осей подвеса. Тем не менее, из-за параллельной ориентации двух осей карданных шарниров нет шарнира, доступного для обеспечения вращения вокруг одной оси, в результате чего подвешенный объект фактически заблокирован (т. е. не может вращаться) вокруг этой оси.

Проблему можно обобщить на другие контексты, где система координат теряет определение одной из своих переменных при определенных значениях других переменных.

Карданы

Карданный подвес — это кольцо, подвешенное таким образом, что оно может вращаться вокруг оси. Карданные подвесы обычно вложены друг в друга, чтобы обеспечить вращение вокруг нескольких осей.

Они появляются в гироскопах и инерциальных измерительных устройствах , чтобы ориентация внутреннего карданного подвеса оставалась фиксированной, в то время как внешний карданный подвес принимает любую ориентацию. В компасах и маховиковых механизмах хранения энергии они позволяют объектам оставаться в вертикальном положении. Они используются для ориентации двигателей на ракетах. ^[1]

Некоторые системы координат в математике ведут себя так, как если бы они были настоящими кардановыми подвесами, используемыми для измерения углов, в частности углов Эйлера .

В случаях с тремя или менее вложенными шарнирами в какой-то момент системы неизбежно происходит их блокировка из-за свойств охватывающих пространств .

В машиностроении

В то время как только две конкретные ориентации обеспечивают точный замок кардана, практические механические карданы сталкиваются с трудностями вблизи этих ориентаций. Когда набор карданов близок к заблокированной конфигурации, небольшие повороты платформы кардана требуют больших движений окружающих карданов. Хотя отношение бесконечно только в точке замка кардана, практические пределы скорости и ускорения карданов — из-за инерции (вытекающей из массы каждого кольца кардана), трения подшипников, сопротивления потоку воздуха или другой жидкости, окружающей карданы (если они не находятся в вакууме), и других физических и инженерных факторов — ограничивают движение платформы вблизи этой точки.

В двух измерениях

Блокировка карданного подвеса может происходить в системах с двумя степенями свободы, таких как теодолит с вращениями вокруг азимута (горизонтальный угол) и угла места (вертикальный угол). Эти двухмерные системы могут блокироваться карданным подвесом в зените и надире , поскольку в этих точках азимут не определен четко, а вращение в направлении азимута не изменяет направление, на которое указывает теодолит.

Рассмотрим отслеживание вертолета, летящего к теодолиту от горизонта. Теодолит — это телескоп, установленный на штативе, так что он может двигаться по азимуту и углу места для отслеживания вертолета. Вертолет летит к теодолиту и отслеживается телескопом по углу места и углу места. Вертолет летит непосредственно над штативом (т. е. он находится в зените), когда он меняет направление и летит под углом 90 градусов к своему предыдущему курсу. Телескоп не может отслеживать этот маневр без прерывистого скачка в одной или обеих ориентациях карданного подвеса. Непрерывного движения, которое позволяет ему следовать за целью, нет. Он находится в карданном захвате. Таким образом, существует бесконечность направлений вокруг зенита, для которых телескоп не может непрерывно отслеживать все движения цели. ^[2] Обратите внимание, что даже если вертолет не проходит через зенит, а только около зенита, так что карданный захват не происходит, система все равно должна двигаться исключительно быстро, чтобы отслеживать его, поскольку он быстро переходит от одного пеленга к другому. Чем ближе к зениту находится ближайшая точка, тем быстрее это должно происходить, и если она действительно проходит через зенит, предел этих «все более быстрых» движений становится бесконечно быстрым, а именно прерывистым.

Чтобы выйти из состояния блокировки подвеса, пользователю необходимо обойти зенит, а именно: уменьшить угол места, изменить азимут так, чтобы он соответствовал азимуту цели, затем изменить угол места так, чтобы он соответствовал цели.

Математически это соответствует тому факту, что сферические координаты не определяют координатную карту на сфере в зените и надире. Альтернативно, соответствующая карта T ² → S ² из тора T ² в сферу S ² (заданную точкой с заданным азимутом и высотой) не является покрывающей картой в этих точках.

В трех измерениях

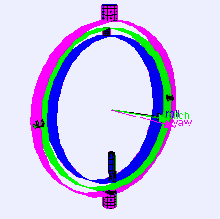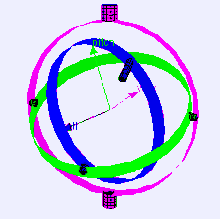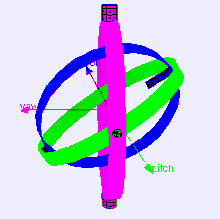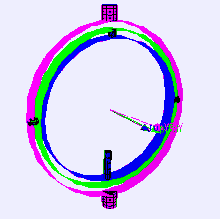
Рассмотрим случай платформы измерения уровня на самолете, летящем строго на север, три оси карданного подвеса которого взаимно перпендикулярны (т. е. углы крена , тангажа и рыскания равны нулю). Если самолет наклоняется на 90 градусов, кардан оси рыскания самолета и платформы становится параллельным кардану оси крена, и изменения относительно рыскания больше не могут быть скомпенсированы.

Решения

Эту проблему можно преодолеть, используя четвертый карданный подвес, активно приводимый в движение двигателем, чтобы поддерживать большой угол между осями крена и рыскания карданного подвеса. Другое решение — повернуть один или несколько карданов в произвольное положение при обнаружении блокировки карданного подвеса и, таким образом, сбросить устройство.

Современная практика заключается в полном отказе от использования карданных подвесов. В контексте инерциальных навигационных систем это можно сделать, монтируя инерциальные датчики непосредственно на корпус транспортного средства (это называется бесплатформенной системой) ^[3] и интегрируя измеренное вращение и ускорение в цифровом виде с использованием методов кватерниона для получения ориентации и скорости транспортного средства. Другой способ замены карданных подвесов — использовать жидкостные подшипники или камеру флотации. ^[4]

На Аполлоне-11

Известный инцидент с замком карданного подвеса произошел во время миссии «Аполлон-11» на Луну. На этом космическом корабле набор карданных подвесов использовался на инерциальном измерительном блоке (IMU). Инженеры знали о проблеме с замком карданного подвеса, но отказались использовать четвертый карданный подвес. ^[5] Некоторые из обоснований этого решения очевидны из следующей цитаты:

Преимущества избыточного карданного подвеса, по-видимому, перевешиваются простотой оборудования, преимуществами в размерах и соответствующей подразумеваемой надежностью прямого блока с тремя степенями свободы.
— Дэвид Хоаг , Apollo Lunar Surface Journal

Они предпочли альтернативное решение, использующее индикатор, который срабатывал бы при наклоне, близком к 85 градусам.

Вблизи этой точки, в замкнутом контуре стабилизации, двигатели крутящего момента теоретически могли бы получить команду мгновенно перевернуть подвес на 180 градусов. Вместо этого, в LM , компьютер выдал предупреждение "блокировка подвеса" на 70 градусах и заморозил IMU на 85 градусах
- Пол Фьелд, журнал Apollo Lunar Surface Journal

Вместо того, чтобы попытаться управлять карданными подвесами быстрее, чем они могли, система просто сдалась и заморозила платформу. С этого момента космический корабль должен был вручную отодвинуться от положения блокировки карданного подвеса, а платформу пришлось бы вручную выровнять, используя звезды в качестве ориентира. ^[6]

После приземления лунного модуля Майк Коллинз , находившийся на борту командного модуля, пошутил: «Как насчет того, чтобы прислать мне на Рождество четвертый шарнир?»

Робототехника

В робототехнике блокировку карданного подвеса обычно называют «переворотом запястья» из-за использования в роботизированных руках «запястья с тройным вращением» , где три оси запястья, управляющие рысканием, тангажом и креном, проходят через общую точку.

Примером переворота запястья, также называемого сингулярностью запястья, является ситуация, когда путь, по которому движется робот, заставляет первую и третью оси запястья робота выровняться. Затем вторая ось запястья пытается повернуться на 180° за нулевое время, чтобы сохранить ориентацию конечного эффектора. Результат сингулярности может быть весьма драматичным и может иметь неблагоприятные последствия для руки робота, конечного эффектора и процесса.

Важность избежания сингулярностей в робототехнике привела к тому, что Американский национальный стандарт для промышленных роботов и робототехнических систем – Требования безопасности определяет их как «состояние, вызванное коллинеарным выравниванием двух или более осей робота, приводящее к непредсказуемым движениям и скоростям робота» ^{[7] .}

В прикладной математике

Проблема блокировки карданного подвеса возникает при использовании углов Эйлера в прикладной математике; разработчики 3D- компьютерных программ , таких как 3D-моделирование , встроенные навигационные системы и видеоигры , должны стараться избегать ее.

На формальном языке, карданный захват происходит из-за того, что отображение из углов Эйлера во вращения (топологически, из 3-тора T ³ в действительное проективное пространство RP ³ , которое совпадает с пространством вращений для трехмерных твердых тел, формально называемым SO(3) ) не является локальным гомеоморфизмом в каждой точке, и, таким образом, в некоторых точках ранг (степени свободы) должен опускаться ниже 3, в этой точке происходит карданный захват. Углы Эйлера предоставляют средство для численного описания любого вращения в трехмерном пространстве с использованием трех чисел, но это описание не только не уникально, но и существуют некоторые точки, где не каждое изменение в целевом пространстве (вращения) может быть реализовано путем изменения в исходном пространстве (углы Эйлера). Это топологическое ограничение — нет покрывающего отображения из 3-тора в 3-мерное действительное проективное пространство; единственная (нетривиальная) покрывающая карта получается из 3-сферы, как при использовании кватернионов .

Для сравнения, все перемещения можно описать с помощью трех чисел , , и , как последовательность трех последовательных линейных движений вдоль трех перпендикулярных осей , и осей. То же самое справедливо и для вращений: все вращения можно описать с помощью трех чисел , , и , как последовательность трех вращательных движений вокруг трех осей, которые перпендикулярны друг другу. Это сходство между линейными координатами и угловыми координатами делает углы Эйлера очень интуитивными , но, к сожалению, они страдают от проблемы карданного замка. $x$ $y$ $z$ $X$ $Y$ $Z$ $\alpha$ $\beta$ $\gamma$

Потеря степени свободы с углами Эйлера

Вращение в трехмерном пространстве может быть представлено численно с помощью матриц несколькими способами. Одно из этих представлений:

{\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}

Пример, который стоит рассмотреть, происходит, когда . Зная, что и , приведенное выше выражение становится равным: $\beta ={\tfrac {\pi }{2}}$ $\cos {\tfrac {\pi }{2}}=0$ $\sin {\tfrac {\pi }{2}}=1$

{\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}

Выполнение умножения матриц :

{\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin \alpha &\cos \alpha &0\\-\cos \alpha &\sin \alpha &0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}&={\begin{bmatrix}0&0&1\\\sin \alpha \cos \gamma +\cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \gamma &0\\-\cos \alpha \cos \gamma +\sin \alpha \sin \gamma &\cos \alpha \sin \gamma +\sin \alpha \cos \gamma &0\end{bmatrix}}\end{aligned}}

И наконец, используя формулы тригонометрии :

{\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin(\alpha +\gamma )&\cos(\alpha +\gamma )&0\\-\cos(\alpha +\gamma )&\sin(\alpha +\gamma )&0\end{bmatrix}}\end{aligned}}

Изменение значений и в приведенной выше матрице имеет тот же эффект: угол поворота изменяется, но ось вращения остается в том же направлении: последний столбец и первая строка в матрице не изменятся. Единственное решение для и для восстановления различных ролей — это изменить . $\alpha$ $\gamma$ $\alpha +\gamma$ $Z$ $\alpha$ $\gamma$ $\beta$

Можно представить себе самолет, вращаемый на вышеупомянутые углы Эйлера, используя соглашение XYZ . В этом случае первый угол - это тангаж. Затем рыскание устанавливается на и окончательное вращение - на - снова является тангажем самолета. Из-за блокировки карданного подвеса он потерял одну из степеней свободы - в данном случае способность к крену. $\alpha$ ${\tfrac {\pi }{2}}$ $\gamma$

Также можно выбрать другое соглашение для представления вращения с помощью матрицы, использующей углы Эйлера, нежели соглашение XYZ, приведенное выше, а также выбрать другие интервалы изменения углов, но в конечном итоге всегда будет по крайней мере одно значение, для которого теряется степень свободы.

Проблема блокировки карданного подвеса не делает углы Эйлера «недействительными» (они всегда служат четко определенной системой координат), но она делает их непригодными для некоторых практических приложений.

Альтернативное представление ориентации

Причиной блокировки карданного подвеса является представление ориентации в вычислениях как трех осевых вращений на основе углов Эйлера. Поэтому потенциальным решением является представление ориентации каким-либо другим способом. Это может быть матрица вращения , кватернион (см. кватернионы и пространственное вращение ) или аналогичное представление ориентации, которое рассматривает ориентацию как значение, а не как три отдельных и связанных значения. При таком представлении пользователь сохраняет ориентацию как значение. Чтобы количественно оценить угловые изменения, произведенные преобразованием, изменение ориентации выражается как дельта-угол/поворот оси. Результирующая ориентация должна быть перенормирована, чтобы предотвратить накопление ошибки с плавающей точкой в последовательных преобразованиях. Для матриц перенормировка результата требует преобразования матрицы в ее ближайшее ортонормированное представление . Для кватернионов перенормировка требует выполнения нормализации кватерниона .

Смотрите также

Диаграммы на SO(3)
Динамика полета – изучение характеристик, устойчивости и управления летательными аппаратами.
Северная сетка – декартова географическая система координат (эквивалентная навигационная задача в полярных экспедициях)
Инерциальная навигационная система – непрерывно вычисляемое счисление пути
Планирование движения – Вычислительная задача
Кватернионы и пространственное вращение – Соответствие между кватернионами и трехмерными вращениями
Проблема «замочной скважины» — проблемы с отслеживанием вблизи оси карданного подвеса при ограничениях по скорости и ускорению.

Ссылки

^ Джонатан Стрикленд (2008). «Что такое карданный подвес — и какое отношение он имеет к НАСА?».
↑ Адриан Попа (4 июня 1998 г.). «Re: Что подразумевается под термином «карданный замок»?».
^ Крис Верплаетсе (1995). "Обзор дизайна пера и основы навигации". Архивировано из оригинала 2009-02-14.
^ Чаппелл, Чарльз, Д. (2006). «Шарнирные газовые опорные площадки».{{cite web}}: CS1 maint: multiple names: authors list (link)
^ Дэвид Хоаг (1963). «Управление и навигация Apollo — соображения по поводу карданного замка IMU Apollo — Документ лаборатории приборостроения Массачусетского технологического института E-1344».
^ Эрик М. Джонс; Пол Фьелд (2006). «Углы подвеса, фиксатор подвеса и четвертый подвес на Рождество».
^ ANSI/RIA R15.06-1999

Внешние ссылки

Gimbal Lock - Объяснение на YouTube