m-арное дерево

Древовидная структура данных, в которой каждый узел имеет не более m дочерних узлов.

Пример m-арного дерева с m=5

В теории графов m - арное дерево (для неотрицательных целых чисел m ) (также известное как n -арное , k -арное или k -путевое дерево) — это древовидное дерево (или, по мнению некоторых авторов, упорядоченное дерево ) ^{[1] [2]} , в котором каждый узел имеет не более m потомков. Бинарное дерево — важный случай, когда  m = 2; аналогично, тернарное дерево — это дерево, где m = 3.

Типым-арные деревья

• Полное m -арное дерево — это m -арное дерево, в котором на каждом уровне каждый узел имеет 0 или m дочерних узлов .
• Полное m -арное дерево ^[3] [ ^4] (или, реже, идеальное m -арное дерево ^[5] ) — это полное m -арное дерево, в котором все листовые узлы находятся на одинаковой глубине.

Свойствам-арные деревья

• Для m -арного дерева высотой h верхняя граница максимального числа листьев равна . ${\displaystyle m^{h}}$
• Высота h m - арного дерева не включает корневой узел, при этом дерево, содержащее только корневой узел, имеет высоту 0.
• Высота дерева равна максимальной глубине D любого узла в дереве.
• Общее число узлов в полном m- арном дереве равно , а высота h равна ${\displaystyle N}$ ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$

$${\displaystyle {\begin{aligned}&{\frac {m^{h+1}-1}{m-1}}\geq N>{\frac {m^{h}-1}{m-1}}\\[8pt]&m^{h+1}\geq (m-1)\cdot N+1>m^{h}\\[8pt]&h+1\geq \log _{m}\left((m-1)\cdot N+1\right)>h\\[8pt]&h\geq \left\lceil \log _{m}((m-1)\cdot N+1)-1\right\rceil .\end{aligned}}}$$По определению Big-Ω максимальная глубина $${\displaystyle D=h\geq \left\lceil \log _{m}((m-1)\cdot N+1)-1\right\rceil =O(\log _{m}n)=O(\log n/\log m).}$$

• Высота полного m -арного дерева с n узлами равна . ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$
• Общее число возможных m -арных деревьев с n узлами равно (что является каталонским числом ). ^[6] ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$

Методы обхода длям-арий деревья

Обход m -арного дерева очень похож на обход бинарного дерева. Прямой обход идет к родительскому, левому поддереву и правому поддереву, а для обратного обхода он идет по левому поддереву, правому поддереву и родительскому узлу. Для обхода в порядке, поскольку на узел приходится более двух потомков при m > 2 , необходимо определить понятия левого и правого поддеревьев. Один из распространенных методов установления левых/правых поддеревьев — разделить список дочерних узлов на две группы. Определив порядок для m потомков узла, первые узлы составят левое поддерево, а узлы составят правое поддерево. ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$

Преобразоватьм-арное дерево в бинарное дерево

Пример преобразования m-арного дерева в бинарное дерево. m=6

Использование массива для представления m- арного дерева неэффективно, поскольку большинство узлов в практических приложениях содержат менее m потомков. В результате этот факт приводит к разреженному массиву с большим неиспользуемым пространством в памяти. Преобразование произвольного m- арного дерева в двоичное дерево увеличит высоту дерева только на постоянный множитель и не повлияет на общую временную сложность в худшем случае. Другими словами, поскольку . ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$

Сначала мы связываем все непосредственные дочерние узлы данного родительского узла вместе, чтобы сформировать список ссылок. Затем мы сохраняем ссылку от родителя к первому (то есть самому левому) дочернему узлу и удаляем все остальные ссылки к остальным дочерним узлам. Мы повторяем этот процесс для всех дочерних узлов (если у них есть дочерние узлы), пока не обработаем все внутренние узлы и не повернем дерево на 45 градусов по часовой стрелке. Полученное дерево является желаемым бинарным деревом, полученным из данного m -арного дерева.

Методы хранениям-арные деревья

Массивы

Пример сохранения m-арного дерева с m=3 в массиве

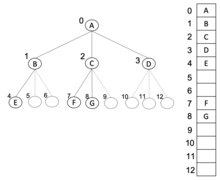
m -арные деревья также могут храниться в порядке "в ширину" как неявная структура данных в массивах , и если дерево является полным m -арным деревом, этот метод не тратит место впустую. В этом компактном расположении, если узел имеет индекс i , его c -ый потомок в диапазоне {1,…, m } находится по индексу , в то время как его родитель (если таковой имеется) находится по индексу (предполагая, что корень имеет нулевой индекс, что означает массив с нулевым индексом). Этот метод выигрывает от более компактного хранения и лучшей локальности ссылок , особенно во время обхода в прямом порядке. Пространственная сложность этого метода составляет . ${\displaystyle m\cdot i+c}$ ${\textstyle \left\lfloor {\frac {i-1}{m}}\right\rfloor }$ ${\displaystyle O(m^{n})}$

На основе указателя

Каждый узел будет иметь внутренний массив для хранения указателей на каждого из своих дочерних узлов: ${\displaystyle m}$

Реализация m-арного дерева на основе указателей, где m = 4.

По сравнению с реализацией на основе массива этот метод реализации имеет превосходящую пространственную сложность . ${\displaystyle O(m\cdot n)}$

Перечислением-арий деревья

Перечисление всех возможных m -арных деревьев полезно во многих дисциплинах как способ проверки гипотез или теорий. Правильное представление объектов m- арного дерева может значительно упростить процесс генерации. Можно построить представление битовой последовательности , используя поиск в глубину m -арного дерева с n узлами, указывающими на наличие узла с заданным индексом, используя двоичные значения. Например, битовая последовательность x=1110000100010001000 представляет собой 3-арное дерево с n=6 узлами, как показано ниже.

3-арное дерево с последовательностью бит 1110000100010001000 и простой нулевой последовательностью 004433

Проблема с этим представлением заключается в том, что перечисление всех строк битов в лексикографическом порядке означало бы, что две последовательные строки могут представлять два дерева, которые лексикографически сильно различаются. Поэтому перечисление по двоичным строкам не обязательно приведет к упорядоченной генерации всех m- арных деревьев. ^[7] Лучшее представление основано на целочисленной строке, которая указывает количество нулей между последовательными единицами, известной как простая нулевая последовательность . — это простая нулевая последовательность, соответствующая битовой последовательности , где j — это количество нулей, необходимых в конце последовательности, чтобы строка имела соответствующую длину. Например, — это простое представление нулевой последовательности на рисунке выше. Более компактным представлением 00433 является , которое называется нулевой последовательностью , в которой дублирующиеся основания не могут быть смежными. Это новое представление позволяет построить следующую допустимую последовательность в . Простая нулевая последовательность допустима, если То есть количество нулей в битовой последовательности m -арного дерева не может превышать общего количества нулевых указателей (т. е. указателей без прикрепленных к ним дочерних узлов). Это суммирование накладывает ограничение на узлы, чтобы было место для добавления без создания недействительной структуры (т.е. имея доступный нулевой указатель для присоединения к нему последнего узла). ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ ${\displaystyle 1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433}$ ${\displaystyle 0^{2}4^{1}3^{2}}$ ${\displaystyle O(1)}$ $${\displaystyle \sum _{i=1}^{i=j}s_{i}\leq (m-1)j\qquad \forall j\leq n-1.}$$ ${\displaystyle n-1}$ ${\displaystyle n^{t}h}$

В таблице ниже представлен список всех допустимых простых нулевых последовательностей всех 3 -арных деревьев с 4 узлами:

Начиная с нижнего правого угла таблицы (т. е. "000"), есть шаблон основы , который управляет генерацией возможных упорядоченных деревьев, начиная с "000" до "006". Шаблон основы для этой группы ("00X") изображен ниже, где дополнительный узел добавляется в позиции, обозначенные "x".

После того, как все возможные позиции в шаблоне основы будут исчерпаны, будет создан новый шаблон путем смещения третьего узла на одну позицию вправо, как показано ниже, и тот же самый подсчет будет выполняться до тех пор, пока все возможные позиции, помеченные «X», не будут исчерпаны.

Возвращаясь к таблице перечисления всех m -арных деревьев, где и , мы можем легко заметить, что кажущийся скачок от «006» до «010» можно объяснить тривиально в алгоритмической форме, как показано ниже: ${\displaystyle m=3}$ ${\displaystyle n=4}$

Псевдокод для этого перечисления приведен ниже: ^[7]

Процедура NEXT( s 1 , s 2 , …, s n −1 ) если  s i = 0 для всех i  то законченный else  i ← max { i | s i > 0} s i ← s i − 1 if  i < n − 1 then  s i ← ( i + 1) ⋅ ( m − 1) − sum( s j ) end if  for  j ← i + 2, i + 3, …, n − 1 s j ← k − 1 end if end

Перечисление без цикла

Алгоритм генерации, который занимает наихудшее время, называется бесцикловым, поскольку временная сложность не может включать цикл или рекурсию. Бесцикловое перечисление m- арных деревьев называется бесцикловым, если после инициализации оно генерирует последовательные объекты деревьев в . Для заданного m -арного дерева T, являющегося одним из его узлов и его -го потомка, поворот налево-t в выполняется путем создания корневого узла и превращения и всех его поддеревьев в потомков , дополнительно мы назначаем самых левых потомков , а самый правый потомок остается прикрепленным к нему, пока повышается до корня, как показано ниже: ${\displaystyle O(1)}$ ${\displaystyle O(1)}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle t}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle m-1}$ ${\displaystyle d}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle d}$

Преобразовать m-арное дерево в левое дерево  для  i = 1... n : для  t = 2... m : пока  t является потомком узла на глубине i ≠ 1: Вращение Lt в узлах на глубине i  заканчивается, пока  конец для  конца для

Вращение вправо-t в точке d является обратной операцией. Левая цепочка T представляет собой последовательность узлов, таких что является корнем, и все узлы, за исключением , имеют одного потомка, соединенного с их самым левым (т. е. ) указателем. Любое m- арное дерево может быть преобразовано в дерево левой цепи с помощью последовательности конечных вращений влево-t для t от 2 до m . В частности, это можно сделать, выполняя вращения влево-t на каждом узле , пока все его поддерево не станут нулевыми на каждой глубине. Затем последовательность числа вращений влево-t, выполненных на глубине i, обозначенная как , определяет кодовое слово m - арного дерева, которое можно восстановить, выполнив ту же последовательность вращений вправо-t. ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{n}}$ ${\displaystyle m[1]}$ ${\displaystyle x_{i}}$ ${\displaystyle m-1}$ ${\displaystyle c_{i}}$

Пусть кортеж представляет собой число вращений L-2 , вращений L-3 , ..., вращений Lm , которые произошли в корне (т.е. i = 1). Тогда — число вращений Lt , требуемых на глубине i . ${\displaystyle m-1}$ ${\displaystyle c_{1},c_{2},\dots ,c_{m-1}}$ ${\displaystyle c_{(i-1)(m-1)+t-1}}$

Сбор количества левых поворотов на каждой глубине является способом кодирования m -арного дерева. Таким образом, перечисление всех возможных допустимых кодировок поможет нам сгенерировать все m -арные деревья для заданных m и n . Но не все последовательности из m неотрицательных целых чисел представляют собой допустимое m-арное дерево. Последовательность неотрицательных целых чисел является допустимым представлением m - арного дерева тогда и только тогда, когда ^[8] ${\displaystyle c_{i}}$ ${\displaystyle (n-1)\cdot (m-1)+1}$ $${\displaystyle \sum _{i=j}^{n}\sum _{t=2}^{m}c_{(i-1)(m-1)+t-1}\qquad \leq n-j,\qquad \forall j\in 0\dots n.}$$

Лексикографически наименьшее кодовое слово, представляющее m-арную последовательность с n узлами, состоит из одних нулей, а наибольшее — из n −1 единиц, за которыми справа следует m −1 нулей.

Инициализация c[i] в ​​ноль для всех i от 1 до n ⋅( k − 1) p[i] установлено в n − 1 для i от 1 до n сумма ← 0 j ← m − 1Условие завершения Завершить, когда c[1] = n − 1Процедура NEXT [8]  сумма ← сумма + 1 − c [ j + 1] c [j] ← c [ j ] + 1 если  p [ q [ j ]] > p [ q [ j + 1]] + 1 тогда  p [ q [ j ]] ← p [ q [ j + 1]] + 1 конец если  p [ q [ j + c [ j ]]] ← p [ q [ j ]] c [ j + 1] ← 0 если  сумма = p [ q [ j ]] тогда  j ← j − 1 иначе  p [ n ] ← сумма  j ← m − 1 конец если конец

Приложение

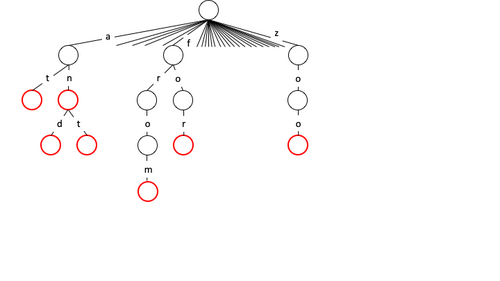
Одним из применений m -арного дерева является создание словаря для проверки допустимых строк. Чтобы сделать это, пусть m будет равно количеству допустимых алфавитов (например, количеству букв английского алфавита ), а корень дерева будет представлять начальную точку. Аналогично, каждый из потомков может иметь до m потомков, представляющих следующий возможный символ в строке. Таким образом, символы вдоль путей могут представлять допустимые ключи, помечая конечный символ ключей как «конечный узел». Например, в примере ниже «at» и «and» являются допустимыми ключевыми строками, а «t» и «d» отмечены как конечные узлы. Конечные узлы могут хранить дополнительную информацию, которая будет связана с данным ключом. Существуют похожие способы построения такого словаря с использованием B-дерева , октадерева и/или trie .

Смотрите также

• Фактор разветвления
• Бинарное дерево «левый потомок — правый брат»
• Двоичное дерево

Ссылки

1. Ли, Лиу (1998). Java: структуры данных и программирование. Раздел 8.1.2.1, Многомерные деревья : Springer. doi :10.1007/978-3-642-95851-9. ISBN 978-3-642-95853-3. S2CID  708416 . Получено 20 июля 2023 г. .{{cite book}}: CS1 maint: location (link)
2. Стэнли, Ричард П. (2011). Перечислительная комбинаторика, том I. Приложение: Терминология теории графов: Cambridge University Press. стр. 573. ISBN 978-1-107-60262-5. Получено 20 июля 2023 г. .
3. Гросс, Джонатан Л.; Йеллен, Джей; Андерсон, Марк (2018). Теория графов и ее приложения (3-е изд.). Раздел 3.2, Корневые деревья, упорядоченные деревья и двоичные деревья : CRC Press. стр. 132. ISBN 978-1-4822-4948-4.{{cite book}}: CS1 maint: location (link)
4. Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Стайн, Клиффорд (2022). Введение в алгоритмы (4-е изд.). Раздел B.5.3, Двоичные и позиционные деревья : MIT Press. стр. 1174. ISBN 9780262046305. Получено 20 июля 2023 г. .{{cite book}}: CS1 maint: location (link)
5. Шумахер, Патрик (2012). «Экскурсия: Теория сетей». Автопоэзис архитектуры: Новая повестка дня для архитектуры, том II. Wiley. стр. 103. ISBN 978-0-470-66616-6.
6. Грэм, Рональд Л.; Кнут, Дональд Э.; Паташник, Орен (1994). Конкретная математика: основа компьютерной науки (2-е изд.). AIP.
7. Baronaigien, Dominique Roelants van (2000). «Генерация K-арных деревьев без циклов». Журнал алгоритмов . 35 (1): 100–107. doi :10.1006/jagm.1999.1073.
8. Korsh, James F (1994). "Бесциклическая генерация последовательностей k-арных деревьев". Information Processing Letters . 52 (5). Elsevier: 243–247. doi :10.1016/0020-0190(94)00149-9.

• Сторер, Джеймс А. (2001). Введение в структуры данных и алгоритмы . Birkhäuser Boston. ISBN 3-7643-4253-6.

Внешние ссылки

• N-арные деревья, Бруно Р. Прейсс, доктор философии, профессор технических наук.