Линейная функция (исчисление)

Полиномиальная функция степени не выше единицы

График линейной функции: ${\displaystyle y(x)=-x+2}$

В исчислении и смежных областях математики линейная функция от действительных чисел до действительных чисел — это функция, график которой (в декартовых координатах ) представляет собой невертикальную линию на плоскости. ^[1] Характерным свойством линейных функций является то, что при изменении входной переменной изменение выходного сигнала пропорционально изменению входного сигнала.

Линейные функции связаны с линейными уравнениями .

Характеристики

Линейная функция — это полиномиальная функция , в которой переменная x имеет степень не выше единицы: ^[2]

${\displaystyle f(x)=ax+b}$.

Такая функция называется линейной, поскольку ее график , множество всех точек декартовой плоскости , представляет собой линию . Коэффициент a называется наклоном функции и линии (см. ниже). ${\displaystyle (x,f(x))}$

Если наклон равен , то это постоянная функция, определяющая горизонтальную линию, которую некоторые авторы исключают из класса линейных функций. ^[3] При таком определении степень линейного полинома будет равна ровно единице, а его график будет прямой, которая не является ни вертикальной, ни горизонтальной. Однако в данной статье требуется, поэтому постоянные функции будут считаться линейными. ${\displaystyle a=0}$ ${\displaystyle f(x)=b}$ ${\displaystyle a\neq 0}$

Если то линейная функция называется однородной . Такая функция определяет прямую, проходящую через начало системы координат, то есть точку . В текстах по высшей математике термин линейная функция часто обозначает именно однородные линейные функции, тогда как термин аффинная функция используется для общего случая, который включает . ${\displaystyle b=0}$ ${\displaystyle (x,y)=(0,0)}$ ${\displaystyle b\neq 0}$

Естественная область определения линейной функции , множество допустимых входных значений для x , представляет собой весь набор действительных чисел . Можно также рассматривать такие функции с x в произвольном поле , взяв коэффициенты a, b в этом поле. ${\displaystyle f(x)}$ ${\displaystyle x\in \mathbb {R} .}$

График представляет собой невертикальную линию, имеющую ровно одно пересечение с осью y , точку пересечения с осью y . Значение пересечения с осью y также называется начальным значением . Если график представляет собой негоризонтальную линию, имеющую ровно одно пересечение с осью x , точку пересечения с осью x . Значение пересечения с осью x решение уравнения также называется корнем или нулем . ${\displaystyle y=f(x)=ax+b}$ ${\displaystyle (x,y)=(0,b).}$ ${\displaystyle y=f(0)=b}$ ${\displaystyle f(x).}$ ${\displaystyle a\neq 0,}$ ${\displaystyle (x,y)=(-{\tfrac {b}{a}},0).}$ ${\displaystyle x=-{\tfrac {b}{a}},}$ ${\displaystyle f(x)=0,}$ ${\displaystyle f(x).}$

Склон

Наклон линии — это отношение между изменением x , обозначаемым , и соответствующим изменением y , обозначаемым ${\displaystyle {\tfrac {\Delta y}{\Delta x}}}$ ${\displaystyle \Delta x}$ ${\displaystyle \Delta y}$

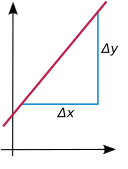
Наклон невертикальной линии — это число, которое измеряет, насколько круто наклонена линия (подъем-переход). Если линия является графиком линейной функции , этот наклон задается константой a . ${\displaystyle f(x)=ax+b}$

Наклон измеряет постоянную скорость изменения на единицу изменения x : всякий раз, когда вход x увеличивается на одну единицу, выход изменяется на a единиц: , и в более общем случае для любого числа . Если наклон положительный, , то функция возрастает; если , то убывает ${\displaystyle f(x)}$ ${\displaystyle f(x{+}1)=f(x)+a}$ ${\displaystyle f(x{+}\Delta x)=f(x)+a\Delta x}$ ${\displaystyle \Delta x}$ ${\displaystyle a>0}$ ${\displaystyle f(x)}$ ${\displaystyle a<0}$ ${\displaystyle f(x)}$

В исчислении производная общей функции измеряет скорость ее изменения. Линейная функция имеет постоянную скорость изменения, равную ее наклону a , поэтому ее производная является постоянной функцией . ${\displaystyle f(x)=ax+b}$ ${\displaystyle f\,'(x)=a}$

Основная идея дифференциального исчисления заключается в том, что любая гладкая функция (не обязательно линейная) может быть близко аппроксимирована вблизи заданной точки единственной линейной функцией. Производная — это наклон этой линейной функции, а аппроксимация равна: для . График линейной аппроксимации — это касательная линия графика в точке . Наклон производной, как правило, меняется вместе с точкой c . Линейные функции можно охарактеризовать как единственные действительные функции, производная которых постоянна: если для всех x , то для . ${\displaystyle f(x)}$ ${\displaystyle x=c}$ ${\displaystyle f\,'(c)}$ ${\displaystyle f(x)\approx f\,'(c)(x{-}c)+f(c)}$ ${\displaystyle x\approx c}$ ${\displaystyle y=f(x)}$ ${\displaystyle (c,f(c))}$ ${\displaystyle f\,'(c)}$ ${\displaystyle f\,'(x)=a}$ ${\displaystyle f(x)=ax+b}$ ${\displaystyle b=f(0)}$

Формы «наклон-пересечение», «точка-наклон» и «двухточечные»

Заданная линейная функция может быть записана в нескольких стандартных формулах, отображающих ее различные свойства. Простейшей является форма наклона-пересечения : ${\displaystyle f(x)}$

${\displaystyle f(x)=ax+b}$,

из которого можно сразу увидеть наклон a и начальное значение , которое является точкой пересечения графика с осью Y. ${\displaystyle f(0)=b}$ ${\displaystyle y=f(x)}$

При наличии наклона a и одного известного значения запишем форму точки-наклона : ${\displaystyle f(x_{0})=y_{0}}$

${\displaystyle f(x)=a(x{-}x_{0})+y_{0}}$.

Графически это дает линию с наклоном , проходящую через точку . ${\displaystyle y=f(x)}$ ${\displaystyle (x_{0},y_{0})}$

Двухточечная форма начинается с двух известных значений и . Вычисляется наклон и вставляется в форму точка-наклон: ${\displaystyle f(x_{0})=y_{0}}$ ${\displaystyle f(x_{1})=y_{1}}$ ${\displaystyle a={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}}$

${\displaystyle f(x)={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x{-}x_{0}\!)+y_{0}}$.

Его график — единственная линия, проходящая через точки . Уравнение можно также записать, чтобы подчеркнуть постоянный наклон: ${\displaystyle y=f(x)}$ ${\displaystyle (x_{0},y_{0}\!),(x_{1},y_{1}\!)}$ ${\displaystyle y=f(x)}$

${\displaystyle {\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}}$.

Связь с линейными уравнениями

Линейные функции обычно возникают из практических задач, включающих переменные с линейной зависимостью, то есть подчиняющиеся линейному уравнению . Если , можно решить это уравнение относительно y , получив ${\displaystyle x,y}$ ${\displaystyle Ax+By=C}$ ${\displaystyle B\neq 0}$

${\displaystyle y=-{\tfrac {A}{B}}x+{\tfrac {C}{B}}=ax+b,}$

где мы обозначаем и . То есть, можно рассматривать y как зависимую переменную (выход), полученную из независимой переменной (вход) x через линейную функцию: . В координатной плоскости xy возможные значения образуют линию, график функции . Если в исходном уравнении результирующая линия вертикальна и не может быть записана как . ${\displaystyle a=-{\tfrac {A}{B}}}$ ${\displaystyle b={\tfrac {C}{B}}}$ ${\displaystyle y=f(x)=ax+b}$ ${\displaystyle (x,y)}$ ${\displaystyle f(x)}$ ${\displaystyle B=0}$ ${\displaystyle x={\tfrac {C}{A}}}$ ${\displaystyle y=f(x)}$

Особенности графика можно интерпретировать в терминах переменных x и y . Точка пересечения с осью y является начальным значением при . Наклон a измеряет скорость изменения выходного сигнала y на единицу изменения входного сигнала x . На графике перемещение на одну единицу вправо (увеличение x на 1) перемещает значение y вверх на a : то есть, . Отрицательный наклон a указывает на уменьшение y при каждом увеличении x . ${\displaystyle y=f(x)=ax+b}$ ${\displaystyle y=f(0)=b}$ ${\displaystyle x=0}$ ${\displaystyle f(x{+}1)=f(x)+a}$

Например, линейная функция имеет наклон , точку пересечения с осью y и точку пересечения с осью x . ${\displaystyle y=-2x+4}$ ${\displaystyle a=-2}$ ${\displaystyle (0,b)=(0,4)}$ ${\displaystyle (2,0)}$

Пример

Предположим, что салями и колбаса стоят €6 и €3 за килограмм, и мы хотим купить на €12. Сколько каждого из них мы можем купить? Если x килограмм салями и y килограмм колбасы стоят в общей сложности €12, то €6× x + €3× y = €12. Решение относительно y дает форму точки-наклона , как указано выше. То есть, если мы сначала выберем количество салями x , количество колбасы можно вычислить как функцию . Поскольку салями стоит вдвое дороже колбасы, добавление одного килограмма салями уменьшает колбасу на 2 килограмма: , а наклон равен −2. Точка пересечения с осью y соответствует покупке всего 4 кг колбасы; тогда как точка пересечения с осью x соответствует покупке всего 2 кг салями. ${\displaystyle y=-2x+4}$ ${\displaystyle y=f(x)=-2x+4}$ ${\displaystyle f(x{+}1)=f(x)-2}$ ${\displaystyle (x,y)=(0,4)}$ ${\displaystyle (x,y)=(2,0)}$

Обратите внимание, что график включает точки с отрицательными значениями x или y , которые не имеют смысла с точки зрения исходных переменных (если только мы не представляем себе продажу мяса мяснику). Таким образом, мы должны ограничить нашу функцию областью . ${\displaystyle f(x)}$ ${\displaystyle 0\leq x\leq 2}$

Кроме того, мы могли бы выбрать y в качестве независимой переменной и вычислить x с помощью обратной линейной функции: по области определения . ${\displaystyle x=g(y)=-{\tfrac {1}{2}}y+2}$ ${\displaystyle 0\leq y\leq 4}$

Связь с другими классами функций

Если коэффициент при переменной не равен нулю ( a ≠ 0 ), то линейная функция представлена ​​полиномом первой степени ( также называемым линейным полиномом ), в противном случае это постоянная функция — также полиномиальная функция, но нулевой степени.

Прямая линия, нарисованная в другой системе координат, может представлять другие функции.

Например, она может представлять собой экспоненциальную функцию , когда ее значения выражены в логарифмической шкале . Это означает, что когда log ( g ( x )) является линейной функцией x , функция g является экспоненциальной. В случае линейных функций увеличение входных данных на одну единицу приводит к увеличению выходных данных на фиксированную величину, которая является наклоном графика функции. В случае экспоненциальных функций увеличение входных данных на одну единицу приводит к увеличению выходных данных на фиксированное кратное, которое известно как основание экспоненциальной функции.

Если и аргументы , и значения функции находятся в логарифмической шкале (т. е. когда log ( y ) является линейной функцией log ( x ) ), то прямая линия представляет собой степенной закон :

${\displaystyle \log _{r}y=a\log _{r}x+b\quad \Rightarrow \quad y=r^{b}\cdot x^{a}}$

Архимедова спираль, определяемая полярным уравнением r = 1 ⁄ 2 θ + 2

С другой стороны, график линейной функции в полярных координатах :

${\displaystyle r=f(\theta )=a\theta +b}$

является архимедовой спиралью, если и окружностью в противном случае. ${\displaystyle a\neq 0}$

Смотрите также

• Аффинное отображение , обобщение
• Арифметическая прогрессия , линейная функция целочисленного аргумента

Примечания

1. Стюарт 2012, стр. 23.
2. Стюарт 2012, стр. 24.
3. Своковски 1983, стр. 34.

Ссылки

• Стюарт, Джеймс (2012), Исчисление: Ранние трансцендентали (7-е изд.), Brooks/Cole, ISBN 978-0-538-49790-9
• Своковски, Эрл В. (1983), Исчисление с аналитической геометрией (Альтернативное издание), Бостон: Prindle, Weber & Schmidt, ISBN 0871503417

Внешние ссылки

• https://web.archive.org/web/20130524101825/http://www.math.okstate.edu/~noell/ebsm/linear.html
• https://web.archive.org/web/20180722042342/https://corestandards.org/assets/CCSSI_Math%20Standards.pdf