Задача о максимальном потоке

Вычислительная задача в теории графов

Сеть потоков для задачи: Каждый человек (r i ) готов взять кошку (w i 1) и/или собаку (w i 2). Однако каждое домашнее животное (p i ) отдает предпочтение только подмножеству людей. Найдите любое соответствие домашних животных людям таким образом, чтобы максимальное количество домашних животных было взято одним из предпочитаемых им людей.

В теории оптимизации задачи максимального потока подразумевают поиск допустимого потока через сеть потоков , который обеспечивает максимально возможную скорость потока.

Проблему максимального потока можно рассматривать как частный случай более сложных проблем сетевых потоков, таких как задача циркуляции . Максимальное значение потока st (т. е. потока из источника s в сток t) равно минимальной пропускной способности разреза st (т. е. разреза, отделяющего s от t) в сети, как указано в теореме о максимальном потоке и минимальном разрезе .

История

Задача о максимальном потоке была впервые сформулирована в 1954 году Т. Э. Харрисом и Ф. С. Россом как упрощенная модель советского железнодорожного транспортного потока. ^{[1] [2] [3]}

В 1955 году Лестер Р. Форд-младший и Делберт Р. Фулкерсон создали первый известный алгоритм — алгоритм Форда–Фулкерсона . ^{[4] [5]} В своей статье 1955 года ^[4] Форд и Фулкерсон написали, что проблема Харриса и Росса формулируется следующим образом (см. ^[1] стр. 5):

Рассмотрим железнодорожную сеть, соединяющую два города через ряд промежуточных городов, где каждому звену сети присвоен номер, представляющий его пропускную способность. Предполагая устойчивое состояние, найдите максимальный поток из одного заданного города в другой.

В своей книге «Потоки в сетях » ^[5] в 1962 году Форд и Фулкерсон писали:

Весной 1955 года этот вопрос был задан авторам Т. Э. Харрисом, который совместно с генералом Ф. С. Россом (в отставке) сформулировал упрощенную модель железнодорожного транспортного потока и обозначил эту конкретную проблему как центральную, предложенную моделью [11].

где [11] относится к секретному отчету 1955 года «Основы метода оценки пропускной способности железнодорожной сети» Харриса и Росса ^[3] (см. ^[1] стр. 5).

За эти годы были обнаружены различные улучшенные решения задачи максимального потока, в частности, алгоритм кратчайшего увеличивающегося пути Эдмондса и Карпа и независимо Диница; алгоритм блокирующего потока Диница; алгоритм push-relabel Голдберга и Тарьяна ; и алгоритм двоичного блокирующего потока Голдберга и Рао. Алгоритмы Шермана ^[6] и Кельнера, Ли, Ореккии и Сидфорда ^{[7] [8]} соответственно находят приблизительно оптимальный максимальный поток, но работают только в неориентированных графах.

В 2013 году Джеймс Б. Орлин опубликовал статью, описывающую алгоритм. ^[9] ${\displaystyle O(|V||E|)}$

В 2022 году Ли Чен, Расмус Кинг, Ян П. Лю, Ричард Пэн, Максимилиан Пробст Гутенберг и Сушант Сачдева опубликовали алгоритм с почти линейным временем работы для задачи потока минимальной стоимости , частным случаем которой является задача максимального потока. ^{[10] [11]} Для задачи кратчайшего пути из одного источника (SSSP) с отрицательными весами также был представлен другой частный случай задачи потока минимальной стоимости — алгоритм с почти линейным временем работы. ^{[12] [13] Оба алгоритма были признаны лучшими докладами на} Симпозиуме по основам компьютерных наук 2022 года . ^{[14] [15]} ${\displaystyle O(|E|^{1+o(1)})}$

Определение

Сеть потоков с источником s и стоком t . Числа рядом с ребрами — пропускные способности.

Сначала введем некоторые обозначения:

• Пусть будет сетью, в которой источник и сток соответственно. ${\displaystyle N=(V,E)}$ ${\displaystyle s,t\in V}$ ${\displaystyle N}$
• Если функция на краях , то ее значение на обозначается как или ${\displaystyle g}$ ${\displaystyle N}$ ${\displaystyle (u,v)\in E}$ ${\displaystyle g_{uv}}$ ${\displaystyle g(u,v).}$

Определение. Пропускная способность ребра — это максимальный объем потока, который может пройти через ребро. Формально это карта ${\displaystyle c:E\to \mathbb {R} ^{+}.}$

Определение. Поток — это карта , которая удовлетворяет следующим условиям: ${\displaystyle f:E\to \mathbb {R} }$

• Ограничение пропускной способности . Поток ребра не может превышать его пропускную способность, другими словами: для всех ${\displaystyle f_{uv}\leq c_{uv}}$ ${\displaystyle (u,v)\in E.}$
• Сохранение потоков. Сумма потоков, входящих в узел, должна равняться сумме потоков, выходящих из этого узла, за исключением источника и стока. Или:

${\displaystyle \forall v\in V\setminus \{s,t\}:\quad \sum _{u:(u,v)\in E,f_{uv}>0}f_{uv}=\sum _{u:(v,u)\in E,f_{vu}>0}f_{vu}.}$

Замечание . Потоки кососимметричны: для всех ${\displaystyle f_{uv}=-f_{vu}}$ ${\displaystyle (u,v)\in E.}$

Определение. Величина потока — это количество потока, проходящего от источника к стоку. Формально для потока это определяется как: ${\displaystyle f:E\to \mathbb {R} ^{+}}$

${\displaystyle |f|=\sum _{v:\ (s,v)\in E}f_{sv}=\sum _{u:\ (u,t)\in E}f_{ut}.}$

Определение. Задача максимального потока заключается в том, чтобы направить как можно больший поток от источника к приемнику, другими словами, найти поток с максимальным значением. ${\displaystyle f_{\textrm {max}}}$

Обратите внимание, что может существовать несколько максимальных потоков, и если разрешены произвольные действительные (или даже произвольные рациональные) значения потока (вместо просто целых чисел), то существует либо ровно один максимальный поток, либо бесконечно много, поскольку существует бесконечно много линейных комбинаций базовых максимальных потоков. Другими словами, если мы отправляем единицы потока по ребру в одном максимальном потоке, а единицы потока по другому максимальному потоку, то для каждого мы можем отправить единицы и направить поток по оставшимся ребрам соответственно, чтобы получить другой максимальный поток. Если значения потока могут быть любыми действительными или рациональными числами, то существует бесконечно много таких значений для каждой пары . ${\displaystyle x}$ ${\displaystyle u}$ ${\displaystyle y>x}$ ${\displaystyle u}$ ${\displaystyle \Delta \in [0,y-x]}$ ${\displaystyle x+\Delta }$ ${\displaystyle u}$ ${\displaystyle \Delta }$ ${\displaystyle x,y}$

Алгоритмы

В следующей таблице перечислены алгоритмы решения задачи максимального потока. Здесь и обозначают количество вершин и ребер сети. Значение относится к наибольшей емкости ребер после масштабирования всех емкостей до целочисленных значений (если сеть содержит иррациональные емкости, может быть бесконечной). ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle U}$ ${\displaystyle U}$

Дополнительные алгоритмы см. в книге Голдберга и Тарьяна (1988).

Теорема интегрального потока

Теорема о интегральном потоке утверждает, что

Если каждое ребро в потоковой сети имеет интегральную пропускную способность, то существует интегральный максимальный поток.

Утверждение заключается не только в том, что значение потока является целым числом, что следует непосредственно из теоремы о максимальном потоке и минимальном разрезе , но и в том, что поток на каждом ребре является целым числом. Это имеет решающее значение для многих комбинаторных приложений (см. ниже), где поток через ребро может кодировать, должен ли элемент, соответствующий этому ребру, быть включен в искомый набор или нет.

Приложение

Проблема максимального потока с несколькими источниками и несколькими стоками

Рис. 4.1.1. Трансформация задачи о максимальном потоке с несколькими источниками и несколькими стоками в задачу о максимальном потоке с одним источником и одним стоком

Учитывая сеть с набором источников и набором стоков вместо только одного источника и одного стока, мы должны найти максимальный поток через . Мы можем преобразовать задачу с несколькими источниками и несколькими стоками в задачу максимального потока, добавив объединенный источник, соединенный с каждой вершиной в , и объединенный сток, соединенный каждой вершиной в (также известный как суперисточник и суперсток ) с бесконечной пропускной способностью на каждом ребре (см. рис. 4.1.1.). ${\displaystyle N=(V,E)}$ ${\displaystyle S=\{s_{1},\ldots ,s_{n}\}}$ ${\displaystyle T=\{t_{1},\ldots ,t_{m}\}}$ ${\displaystyle N}$ ${\displaystyle S}$ ${\displaystyle T}$

Двудольное паросочетание с максимальной мощностью

Рис. 4.3.1.Трансформация задачи максимального двудольного паросочетания в задачу максимального потока

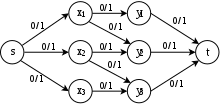
Учитывая двудольный граф , мы должны найти паросочетание максимальной мощности в , то есть паросочетание, которое содержит наибольшее возможное число ребер. Эту задачу можно преобразовать в задачу максимального потока, построив сеть , где ${\displaystyle G=(X\cup Y,E)}$ ${\displaystyle G}$ ${\displaystyle N=(X\cup Y\cup \{s,t\},E')}$

1. ${\displaystyle E'}$содержит ребра, направленные от к . ${\displaystyle G}$ ${\displaystyle X}$ ${\displaystyle Y}$
2. ${\displaystyle (s,x)\in E'}$для каждого и для каждого . ${\displaystyle x\in X}$ ${\displaystyle (y,t)\in E'}$ ${\displaystyle y\in Y}$
3. ${\displaystyle c(e)=1}$для каждого (см. рис. 4.3.1). ${\displaystyle e\in E'}$

Тогда значение максимального потока в равно размеру максимального паросочетания в , а паросочетание максимальной мощности можно найти, взяв те ребра, поток по которым является целочисленным максимальным потоком. ${\displaystyle N}$ ${\displaystyle G}$ ${\displaystyle 1}$

Минимальное покрытие пути в направленном ациклическом графе

Учитывая направленный ациклический граф , мы должны найти минимальное число вершинно-непересекающихся путей для покрытия каждой вершины в . Мы можем построить двудольный граф из , где ${\displaystyle G=(V,E)}$ ${\displaystyle V}$ ${\displaystyle G'=(V_{\textrm {out}}\cup V_{\textrm {in}},E')}$ ${\displaystyle G}$

1. ${\displaystyle V_{\textrm {out}}=\{v_{\textrm {out}}\mid v\in V\land v{\text{ has outgoing edge(s)}}\}}$
2. ${\displaystyle V_{\textrm {in}}=\{v_{\textrm {in}}\mid v\in V\land v{\text{ has incoming edge(s)}}\}}$
3. ${\displaystyle E'=\{(u_{\textrm {out}},v_{\textrm {in}})\in V_{out}\times V_{in}\mid (u,v)\in E\}}$.

Тогда можно показать, что имеет паросочетание размера тогда и только тогда, когда имеет вершинно-непересекающееся покрытие путей, содержащее ребра и пути, где — число вершин в . Таким образом, задачу можно решить, найдя вместо этого паросочетание максимальной мощности в . ${\displaystyle G'}$ ${\displaystyle M}$ ${\displaystyle m}$ ${\displaystyle G}$ ${\displaystyle C}$ ${\displaystyle m}$ ${\displaystyle n-m}$ ${\displaystyle n}$ ${\displaystyle G}$ ${\displaystyle G'}$

Предположим, что мы нашли соответствие и построили из него покрытие . Интуитивно понятно, что если две вершины сопоставлены в , то ребро содержится в . Очевидно, что число ребер в равно . Чтобы увидеть, что является вершинно-непересекающимся, рассмотрим следующее: ${\displaystyle M}$ ${\displaystyle G'}$ ${\displaystyle C}$ ${\displaystyle u_{\mathrm {out} },v_{\mathrm {in} }}$ ${\displaystyle M}$ ${\displaystyle (u,v)}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle m}$ ${\displaystyle C}$

1. Каждая вершина в может быть либо не сопоставлена ​​в , в этом случае нет ребер, выходящих из ; либо она может быть сопоставлена ​​, в этом случае есть ровно одно ребро, выходящее из . В любом случае не более одного ребра покидает любую вершину в . ${\displaystyle v_{\textrm {out}}}$ ${\displaystyle G'}$ ${\displaystyle M}$ ${\displaystyle v}$ ${\displaystyle C}$ ${\displaystyle v}$ ${\displaystyle C}$ ${\displaystyle v}$ ${\displaystyle C}$
2. Аналогично для каждой вершины в – если она сопоставлена, то в нее есть одно входящее ребро ; в противном случае в нее нет входящих ребер . ${\displaystyle v_{\textrm {in}}}$ ${\displaystyle G'}$ ${\displaystyle v}$ ${\displaystyle C}$ ${\displaystyle v}$ ${\displaystyle C}$

Таким образом, ни одна вершина не имеет двух входящих или двух исходящих ребер в , что означает, что все пути в не пересекаются по вершинам. ${\displaystyle C}$ ${\displaystyle C}$

Чтобы показать, что покрытие имеет размер , мы начинаем с пустого покрытия и строим его постепенно. Чтобы добавить вершину к покрытию, мы можем либо добавить ее к существующему пути, либо создать новый путь нулевой длины, начинающийся с этой вершины. Первый случай применим всякий раз, когда либо и какой-то путь в покрытии начинается в , либо и какой-то путь заканчивается в . Последний случай применим всегда. В первом случае общее количество ребер в покрытии увеличивается на 1, а количество путей остается прежним; во втором случае количество путей увеличивается, а количество ребер остается прежним. Теперь ясно, что после покрытия всех вершин сумма количества путей и ребер в покрытии равна . Следовательно, если количество ребер в покрытии равно , то количество путей равно . ${\displaystyle C}$ ${\displaystyle n-m}$ ${\displaystyle u}$ ${\displaystyle (u,v)\in E}$ ${\displaystyle v}$ ${\displaystyle (v,u)\in E}$ ${\displaystyle v}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle n-m}$

Максимальный поток с вершинными мощностями

Рис. 4.4.1.Трансформация задачи максимального потока с ограничением пропускной способности вершин в исходную задачу максимального потока путем разбиения узлов

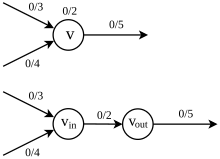
Пусть будет сетью. Предположим, что в каждом узле есть емкость в дополнение к емкости ребра, то есть отображение , при котором поток должен удовлетворять не только ограничению емкости и сохранению потоков, но и ограничению емкости вершины ${\displaystyle N=(V,E)}$ ${\displaystyle c:V\to \mathbb {R} ^{+},}$ ${\displaystyle f}$

${\displaystyle \sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}.}$

Другими словами, величина потока, проходящего через вершину, не может превышать ее пропускную способность. Чтобы найти максимальный поток через , мы можем преобразовать задачу в задачу максимального потока в исходном смысле, расширив . Сначала каждая заменяется на и , где соединена ребрами, входящими в и соединена с ребрами, выходящими из , затем назначаем пропускную способность ребру, соединяющему и (см. рис. 4.4.1). В этой расширенной сети ограничение пропускной способности вершины снимается, и поэтому задачу можно рассматривать как исходную задачу максимального потока. ${\displaystyle N}$ ${\displaystyle N}$ ${\displaystyle v\in V}$ ${\displaystyle v_{\text{in}}}$ ${\displaystyle v_{\text{out}}}$ ${\displaystyle v_{\text{in}}}$ ${\displaystyle v}$ ${\displaystyle v_{\text{out}}}$ ${\displaystyle v}$ ${\displaystyle c(v)}$ ${\displaystyle v_{\text{in}}}$ ${\displaystyle v_{\text{out}}}$

Максимальное количество путей из s в t

Дан ориентированный граф и две вершины и , нам нужно найти максимальное количество путей из в . Эта задача имеет несколько вариантов: ${\displaystyle G=(V,E)}$ ${\displaystyle s}$ ${\displaystyle t}$ ${\displaystyle s}$ ${\displaystyle t}$

1. Пути должны быть непересекающимися по ребрам. Эту задачу можно преобразовать в задачу максимального потока, построив сеть из , где и являются источником и стоком соответственно, и назначив каждому ребру пропускную способность . В этой сети максимальный поток равен , если и только если существуют пути, непересекающиеся по ребрам. ${\displaystyle N=(V,E)}$ ${\displaystyle G}$ ${\displaystyle s}$ ${\displaystyle t}$ ${\displaystyle N}$ ${\displaystyle 1}$ ${\displaystyle k}$ ${\displaystyle k}$

2. Пути должны быть независимыми, т.е. вершинно-непересекающимися (за исключением и ). Мы можем построить сеть из с пропускными способностями вершин, где пропускные способности всех вершин и всех ребер равны . Тогда значение максимального потока равно максимальному числу независимых путей из в . ${\displaystyle s}$ ${\displaystyle t}$ ${\displaystyle N=(V,E)}$ ${\displaystyle G}$ ${\displaystyle 1}$ ${\displaystyle s}$ ${\displaystyle t}$

3. В дополнение к тому, что пути не пересекаются по ребрам и/или вершинам, пути также имеют ограничение по длине: мы учитываем только те пути, длина которых точно равна или не превышает . Большинство вариантов этой задачи являются NP-полными, за исключением небольших значений . ^[27] ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$

Проблема закрытия

Замыкание ориентированного графа — это множество вершин C , такое, что ни одно ребро не покидает C . Задача замыкания — это задача нахождения замыкания с максимальным или минимальным весом в ориентированном графе со взвешенными вершинами. Она может быть решена за полиномиальное время с использованием сведения к задаче максимального потока.

Реальные приложения

Бейсбол выбывание

Построение сетевого потока для задачи исключения бейсбола

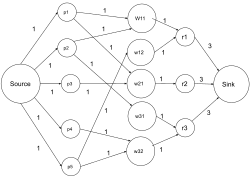
В задаче на выбывание в бейсболе есть n команд, соревнующихся в лиге. На определенном этапе сезона лиги w _i — это количество побед, r _i — это количество игр, оставшихся для игры за команду i, а r _ij — это количество игр, оставшихся против команды j . Команда выбывает, если у нее нет шансов закончить сезон на первом месте. Задача задачи на выбывание в бейсболе — определить, какие команды выбывают в каждой точке сезона. Шварц ^[28] предложил метод, который сводит эту задачу к максимальному сетевому потоку. В этом методе создается сеть для определения того, выбывает ли команда k .

Пусть G = ( V , E ) будет сетью, в которой s , t ∈ V являются источником и стоком соответственно. Добавляется игровой узел _ij – который представляет собой количество игр между этими двумя командами. Мы также добавляем командный узел для каждой команды и соединяем каждый игровой узел { i , j } с i < j с V , и соединяем каждый из них из s ребром с пропускной способностью r _ij – который представляет собой количество игр между этими двумя командами. Мы также добавляем командный узел для каждой команды и соединяем каждый игровой узел { i , j } с двумя командными узлами i и j , чтобы гарантировать победу одного из них. Не нужно ограничивать значение потока на этих ребрах. Наконец, ребра сделаны от командного узла i до приемного узла t , а пропускная способность w _k + r _k – w _i установлена ​​так, чтобы команда i не выиграла больше, чем w _k + r _k . Пусть S будет множеством всех команд, участвующих в лиге, и пусть

${\displaystyle r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\} \atop i<j}r_{ij}}$.

В этом методе утверждается, что команда k не исключается тогда и только тогда, когда в сети G существует значение потока размера r ( S − { k }) . В упомянутой статье доказано, что это значение потока является максимальным значением потока из s в t .

Расписание рейсов авиакомпании

В авиационной отрасли одной из основных проблем является планирование работы экипажей. Задача планирования работы авиакомпаний может рассматриваться как приложение расширенного максимального сетевого потока. Входными данными этой задачи является набор рейсов F , содержащий информацию о том, где и когда каждый рейс отправляется и прибывает. В одной из версий планирования работы авиакомпаний цель состоит в том, чтобы составить допустимое расписание с не более чем k экипажами.

Для решения этой проблемы используется вариация задачи циркуляции, называемая ограниченной циркуляцией, которая является обобщением задач сетевых потоков с дополнительным ограничением в виде нижней границы потоков на ребрах.

Пусть G = ( V , E ) будет сетью с s , t ∈ V в качестве исходного и приемного узлов. Для исходного и конечного узлов каждого рейса i добавляются два узла к V , узел s _i как исходный и узел d _i как конечный узел рейса i . Также добавляются следующие ребра к E :

1. Ребро с пропускной способностью [0, 1] между _s и каждым si .
2. Ребро с пропускной способностью [0, 1] между каждым d _i и t .
3. Ребро с пропускной способностью [1, 1] между каждой _парой si и d _i .
4. Ребро с пропускной способностью [0, 1] между каждым d _i и s _j , если источник s _j достижим за разумное время и стоимость от пункта назначения рейса i .
5. Ребро с пропускной способностью [0, ∞ ] между s и t .

В упомянутом методе утверждается и доказывается, что нахождение значения потока k в G между s и t равнозначно нахождению допустимого расписания для набора полетов F с не более чем k экипажами. ^[29]

Другой вариант планирования авиалиний заключается в поиске минимально необходимого экипажа для выполнения всех рейсов. Чтобы найти ответ на эту задачу, создается двудольный граф G' = ( A ∪ B , E ) , где каждый рейс имеет копию в множестве A и множестве B . Если тот же самолет может выполнить рейс j после рейса i , i ∈ A соединяется с j ∈ B . Сопоставление в G' индуцирует расписание для F и, очевидно, максимальное двудольное сопоставление в этом графе создает расписание авиалиний с минимальным количеством экипажей. ^[29] Как упоминалось в части «Приложение» этой статьи, максимальное кардинальность двудольного сопоставления является приложением задачи максимального потока.

Проблема спроса и обращения

Есть несколько фабрик, которые производят товары, и несколько деревень, куда эти товары должны быть доставлены. Они соединены сетью дорог, каждая из которых имеет пропускную способность c для максимального количества товаров, которые могут по ней пройти. Задача состоит в том, чтобы найти, есть ли циркуляция, которая удовлетворяет спрос. Эту задачу можно преобразовать в задачу максимального потока.

1. Добавьте исходный узел s и добавьте ребра от него к каждому узлу фабрики f _i с производительностью p _{i ,} где p _i — производительность фабрики f _i .
2. Добавьте узел стока t и добавьте ребра из всех деревень v _i в t с пропускной способностью d _{i ,} где d _i — уровень спроса деревни v _i .

Пусть G = ( V , E ) будет этой новой сетью. Существует циркуляция, которая удовлетворяет спрос, если и только если:

Максимальное значение расхода ( G ) . ${\displaystyle =\sum _{i\in v}d_{i}}$

Если циркуляция существует, то рассмотрение решения о максимальном потоке даст ответ на вопрос, сколько товаров необходимо отправить по конкретной дороге для удовлетворения спроса.

Проблему можно расширить, добавив нижнюю границу потока на некоторых ребрах. ^[30]

Сегментация изображения

Исходное изображение размером 8x8.

Сеть, построенная из битовой карты. Источник находится слева, сток справа. Чем темнее край, тем больше его емкость. a _i имеет высокий уровень, когда пиксель зеленый, b _{i —} когда пиксель не зеленый. Штрафы p _ij все равны. ^[31]

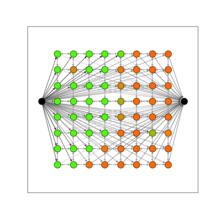
В своей книге Клейнберг и Тардос представляют алгоритм сегментации изображения. ^[32] Они представляют алгоритм для поиска фона и переднего плана на изображении. Точнее, алгоритм принимает в качестве входных данных растровое изображение, смоделированное следующим образом: a _i ≥ 0 — вероятность того, что пиксель i принадлежит переднему плану, b _i ≥ 0 — вероятность того, что пиксель i принадлежит фону, а p _ij — штраф, если два соседних пикселя i и j помещены один на передний план, а другой на задний план. Цель состоит в том, чтобы найти разбиение ( A , B ) набора пикселей, которое максимизирует следующее количество

${\displaystyle q(A,B)=\sum _{i\in A}a_{i}+\sum _{i\in B}b_{i}-\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}}$,

Действительно, для пикселей в A (рассматриваемых как передний план) мы получаем a _i ; для всех пикселей в B (рассматриваемых как фон) мы получаем b _i . На границе, между двумя соседними пикселями i и j , мы теряем p _ij . Это эквивалентно минимизации величины

${\displaystyle q'(A,B)=\sum _{i\in A}b_{i}+\sum _{i\in B}a_{i}+\sum _{\begin{matrix}i,j{\text{ adjacent}}\\|A\cap \{i,j\}|=1\end{matrix}}p_{ij}}$

потому что

${\displaystyle q(A,B)=\sum _{i\in A\cup B}a_{i}+\sum _{i\in A\cup B}b_{i}-q'(A,B).}$

Минимальный разрез отображается в сети (треугольники VS круги).

Теперь мы строим сеть, узлами которой являются пиксель, а также источник и сток, см. рисунок справа. Мы соединяем источник с пикселем i ребром веса a _i . Мы соединяем пиксель i со стоком ребром веса b _i . Мы соединяем пиксель i с пикселем j с весом p _ij . Теперь осталось вычислить минимальный разрез в этой сети (или, что эквивалентно, максимальный поток). На последнем рисунке показан минимальный разрез.

Расширения

1. В задаче о потоке минимальной стоимости каждое ребро ( u ,v) также имеет коэффициент стоимости a _uv в дополнение к своей пропускной способности. Если поток через ребро равен f _uv , то общая стоимость равна a _uv f _uv . Требуется найти поток заданного размера d с наименьшей стоимостью. В большинстве вариантов коэффициенты стоимости могут быть как положительными, так и отрицательными. Для этой задачи существуют различные алгоритмы с полиномиальным временем.

2. Задача максимального потока может быть дополнена дизъюнктивными ограничениями : отрицательное дизъюнктивное ограничение говорит, что определенная пара ребер не может одновременно иметь ненулевой поток; положительное дизъюнктивное ограничение говорит, что в определенной паре ребер по крайней мере одно должно иметь ненулевой поток. С отрицательными ограничениями задача становится сильно NP-трудной даже для простых сетей. С положительными ограничениями задача является полиномиальной, если допускаются дробные потоки, но может быть сильно NP-трудной, когда потоки должны быть целыми. ^[33]

Ссылки

1. Schrijver, A. (2002). «Об истории проблем транспортировки и максимального потока». Математическое программирование . 91 (3): 437–445. CiteSeerX  10.1.1.23.5134 . doi :10.1007/s101070100259. S2CID  10210675.
2. Гасс, Саул И.; Ассад, Арджанг А. (2005). «Математические, алгоритмические и профессиональные разработки исследования операций с 1951 по 1956 год». Аннотированная хронология исследования операций . Международная серия по исследованию операций и науке управления. Том 75. С. 79–110. doi :10.1007/0-387-25837-X_5. ISBN 978-1-4020-8116-3.
3. Harris, TE ; Ross, FS (1955). "Основы метода оценки пропускной способности железнодорожной сети" (PDF) . Исследовательский меморандум . Архивировано из оригинала (PDF) 8 января 2014 г.
4. Ford, LR ; Fulkerson, DR (1956). «Максимальный поток через сеть». Canadian Journal of Mathematics . 8 : 399–404. doi : 10.4153/CJM-1956-045-5 .
5. Форд, Л.Р., младший; Фулкерсон, Д.Р., Потоки в сетях , Издательство Принстонского университета (1962).
6. Шерман, Джона (2013). «Почти максимальные потоки за почти линейное время». Труды 54-го ежегодного симпозиума IEEE по основам компьютерной науки . С. 263–269. arXiv : 1304.2077 . doi : 10.1109/FOCS.2013.36. ISBN 978-0-7695-5135-7. S2CID  14681906.
7. Кельнер, JA; Ли, YT; Ореккия, L.; Сидфорд, A. (2014). "Почти линейный по времени алгоритм для приближенного максимального потока в неориентированных графах и его многопродуктовые обобщения" (PDF) . Труды двадцать пятого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам . стр. 217. arXiv : 1304.2338 . doi : 10.1137/1.9781611973402.16. ISBN 978-1-61197-338-9. S2CID  10733914. Архивировано из оригинала (PDF) 3 марта 2016 г.
8. Найт, Хелен (7 января 2014 г.). «Новый алгоритм может значительно упростить решения проблемы «максимального потока»». MIT News . Получено 8 января 2014 г.
9. Orlin, James B. (2013). "Max flows in O(nm) time, or better". Труды сорок пятого ежегодного симпозиума ACM по теории вычислений . стр. 765–774. CiteSeerX 10.1.1.259.5759 . doi :10.1145/2488608.2488705. ISBN  9781450320290. S2CID  207205207.
10. Chen, L.; Kyng, R.; Liu, YP; Gutenberg, MP; Sachdeva, S. (2022). «Максимальный поток и поток с минимальной стоимостью за почти линейное время». arXiv : 2203.00671 [cs.DS].
11. Кларрайх, Эрика (8 июня 2022 г.). «Исследователи достигли „абсурдно быстрого“ алгоритма для сетевого потока». Журнал Quanta . Получено 8 июня 2022 г.
12. Бернстайн, Аарон; Нанонгкай, Данупон; Вульф-Нильсен, Кристиан (30 октября 2022 г.). «Кратчайшие пути с одним источником и отрицательным весом за почти линейное время». arXiv : 2203.03456 [cs.DS].
13. Брубейкер, Бен (18 января 2023 г.). «Наконец-то, быстрый алгоритм для кратчайших путей на отрицательных графах». Журнал Quanta . Получено 25 января 2023 г.
14. "FOCS 2022". focs2022.eecs.berkeley.edu . Получено 25 января 2023 г. .
15. Сантош, Нагаракатте. «Премия FOCS 2022 за лучшую статью профессора Аарона Бернстайна». www.cs.rutgers.edu . Получено 25 января 2023 г.
16. Малхотра, В. М.; Кумар, М. Прамодх; Махешвари, С. Н. (1978). "Алгоритм O ( | V | 3 ) {\displaystyle O(|V|^{3})} для поиска максимальных потоков в сетях" (PDF) . Information Processing Letters . 7 (6): 277–278. doi :10.1016/0020-0190(78)90016-9.
17. Goldberg, AV ; Tarjan, RE (1988). "Новый подход к проблеме максимального потока". Journal of the ACM . 35 (4): 921. doi : 10.1145/48014.61051 . S2CID  52152408.
18. Cheriyan, J.; Maheshwari, SN (1988). "Анализ алгоритмов проталкивания предпотока для максимального сетевого потока". Основы технологии программного обеспечения и теоретической информатики . Конспект лекций по информатике. Том 338. С. 30–48. doi :10.1007/3-540-50517-2_69. ISBN 978-3-540-50517-4. ISSN  0302-9743.
19. Кинг, В.; Рао, С.; Тарьян, Р. (1994). «Более быстрый детерминированный алгоритм максимального потока». Журнал алгоритмов . 17 (3): 447–474. doi :10.1006/jagm.1994.1044. S2CID  15493.
20. Голдберг, А. В.; Рао, С. (1998). «За барьером разложения потока». Журнал ACM . 45 (5): 783. doi : 10.1145/290179.290181 . S2CID  96030.
21. Kathuria, T.; Liu, YP; Sidford, A. (16–19 ноября 2020 г.). Единичная пропускная способность Maxflow в почти сжатые сроки . Дарем, Северная Каролина, США: IEEE. стр. 119–130. ${\displaystyle O(m^{4/3})}$
22. Мадри, Александр (9–11 октября 2016 г.). Вычисление максимального потока с помощью увеличивающихся электрических потоков . Нью-Брансуик, Нью-Джерси: IEEE. стр. 593–602.
23. Брэнд, Дж. В.Д.; Ли, Ю.Т.; Нанонгкай, Д.; Пэн, Р.; Саранурак, Т.; Сидфорд, А.; Песня, З.; Ван, Д. (16–19 ноября 2020 г.). Двудольное сопоставление за почти линейное время на умеренно плотных графах . Дарем, Северная Каролина, США: IEEE. стр. 919–930.
24. Brand, J. vd; Lee, YT; Liu, YP; Saranurak, T.; Sidford, A; Song, Z.; Wang, D. (2021). «Потоки минимальной стоимости, MDP и ℓ1-регрессия за почти линейное время для плотных экземпляров». arXiv : 2101.05719 [cs.DS].
25. Гао, Y.; Лю, YP; Пэн, R. (2021). «Полностью динамические электрические потоки: разреженный максимальный поток быстрее, чем Голдберг-Рао». arXiv : 2101.07233 [cs.DS].
26. Бернштейн, А.; Бликстад, Дж.; Саранурак, Т.; Ту, Т. (2024). «Максимальный поток за счет увеличения путей во времени». arXiv : 2406.03648 [cs.DS]. ${\displaystyle n^{2+o(1)}}$
27. Итай, А.; Перл, И.; Шилоах, И. (1982). «Сложность поиска максимально непересекающихся путей с ограничениями длины». Networks . 12 (3): 277–286. doi :10.1002/net.3230120306. ISSN  1097-0037.
28. Шварц, Б. Л. (1966). «Возможные победители частично завершенных турниров». Обзор SIAM . 8 (3): 302–308. Bibcode : 1966SIAMR...8..302S. doi : 10.1137/1008062. JSTOR  2028206.
29. Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest и Clifford Stein (2001). "26. Максимальный поток". Введение в алгоритмы, второе издание . MIT Press и McGraw-Hill. стр. 643–668. ISBN 978-0-262-03293-3.{{cite book}}: CS1 maint: multiple names: authors list (link)
30. Карл Кингсфорд. «Расширения максимального потока: циркуляции со спросом» (PDF) .
31. "Проект imagesegmentationwithmaxflow, содержащий исходный код для создания этих иллюстраций". GitLab . Архивировано из оригинала 22 декабря 2019 г. Получено 22 декабря 2019 г.
32. "Algorithm Design". pearson.com . Получено 21 декабря 2019 .
33. Шауэр, Иоахим; Пферши, Ульрих (1 июля 2013 г.). «Проблема максимального потока с дизъюнктивными ограничениями». Журнал комбинаторной оптимизации . 26 (1): 109–119. CiteSeerX 10.1.1.414.4496 . doi :10.1007/s10878-011-9438-7. ISSN  1382-6905. S2CID  6598669. 

Дальнейшее чтение

• Джозеф Чериян и Курт Мельхорн (1999). «Анализ правила выбора самого высокого уровня в алгоритме максимального потока с проталкиванием предпотока». Information Processing Letters . 69 (5): 239–242. CiteSeerX  10.1.1.42.8563 . doi :10.1016/S0020-0190(99)00019-8.
• Daniel D. Sleator и Robert E. Tarjan (1983). "Структура данных для динамических деревьев" (PDF) . Журнал компьютерных и системных наук . 26 (3): 362–391. doi :10.1016/0022-0000(83)90006-5. ISSN  0022-0000.
• Юджин Лоулер (2001). "4. Сетевые потоки". Комбинаторная оптимизация: сети и матроиды . Дувр. стр. 109–177. ISBN 978-0-486-41453-9.