Алгоритмы слияния — это семейство алгоритмов , которые принимают несколько отсортированных списков в качестве входных данных и производят один список в качестве выходных данных, содержащий все элементы списков входных данных в отсортированном порядке. Эти алгоритмы используются в качестве подпрограмм в различных алгоритмах сортировки , наиболее известная из которых — сортировка слиянием .
Алгоритм слияния играет важную роль в алгоритме сортировки слиянием , алгоритме сортировки на основе сравнения . Концептуально алгоритм сортировки слиянием состоит из двух шагов:
Алгоритм слияния многократно используется в алгоритме сортировки слиянием.
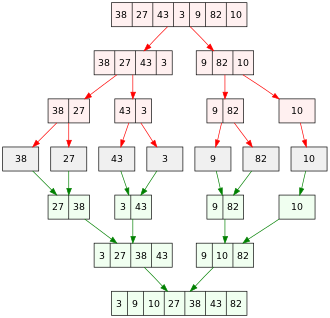
Пример сортировки слиянием показан на иллюстрации. Она начинается с несортированного массива из 7 целых чисел. Массив делится на 7 разделов; каждый раздел содержит 1 элемент и сортируется. Затем сортированные разделы объединяются для получения более крупных сортированных разделов, пока не останется 1 раздел — сортированный массив.
Объединение двух отсортированных списков в один может быть выполнено за линейное время и линейное или постоянное пространство (в зависимости от модели доступа к данным). Следующий псевдокод демонстрирует алгоритм, который объединяет входные списки ( связанные списки или массивы ) A и B в новый список C . [1] [2] : 104 Функция head возвращает первый элемент списка; «удаление» элемента означает его удаление из списка, как правило, путем увеличения указателя или индекса.
алгоритм merge(A, B) — это входные данные A, B : список возвращает список C := новый пустой список пока A не пусто и B не пусто do if head(A) ≤ head(B) then добавить заголовок (A) к C опустите голову А еще добавить заголовок (B) к C опустить голову B // К настоящему моменту либо A, либо B пусты. Осталось очистить другой входной список. пока A не пусто do добавить заголовок (A) к C опустите голову А пока B не пусто делать добавить заголовок (B) к C опустить голову B возврат С
Если входные данные представляют собой связанные списки, этот алгоритм можно реализовать так, чтобы использовать только постоянный объем рабочего пространства; указатели в узлах списков можно повторно использовать для учета и построения окончательного объединенного списка.
В алгоритме сортировки слиянием эта подпрограмма обычно используется для слияния двух подмассивов A[lo..mid] , A[mid+1..hi] одного массива A . Это можно сделать, скопировав подмассивы во временный массив, а затем применив алгоритм слияния, описанный выше. [1] Выделения временного массива можно избежать, но за счет скорости и простоты программирования. Были разработаны различные алгоритмы слияния на месте, [3] иногда жертвуя линейной границей времени для получения алгоритма O ( n log n ) ; [4] см. раздел Сортировка слиянием § Варианты для обсуждения.
k -way mergeing обобщает бинарное слияние до произвольного числа k отсортированных списков входных данных. Приложения k -way mergeing возникают в различных алгоритмах сортировки, включая сортировку с терпением [5] и внешний алгоритм сортировки , который делит свой вход на k = 1/М − 1 блоков, которые помещаются в памяти, сортирует их один за другим, затем объединяет эти блоки. [2] : 119–120
Существует несколько решений этой проблемы. Наивное решение — сделать цикл по k спискам, чтобы каждый раз выбирать минимальный элемент, и повторять этот цикл, пока все списки не опустеют:
В худшем случае этот алгоритм выполняет ( k −1)( n − к/2 ) сравнений элементов для выполнения своей работы, если в спискахвсего n элементов. [6] Его можно улучшить, сохранив списки в приоритетной очереди ( min-heap ), ключом которой является их первый элемент:
Поиск следующего наименьшего элемента для вывода (find-min) и восстановление порядка кучи теперь можно выполнить за время O (log k ) (точнее, за 2⌊log k ⌋ сравнений [6] ), а полную задачу можно решить за время O ( n log k ) (приблизительно за 2 n ⌊log k ⌋ сравнений). [6] [2] : 119–120
Третий алгоритм решения проблемы — это решение «разделяй и властвуй» , которое основано на алгоритме бинарного слияния:
Когда входные списки для этого алгоритма упорядочены по длине, начиная с самых коротких, требуется менее n ⌈log k ⌉ сравнений, т. е. менее половины числа, используемого алгоритмом на основе кучи; на практике он может быть примерно таким же быстрым или медленным, как алгоритм на основе кучи. [6]
Параллельная версия алгоритма бинарного слияния может служить строительным блоком параллельной сортировки слиянием . Следующий псевдокод демонстрирует этот алгоритм в параллельном стиле «разделяй и властвуй» (адаптирован из Cormen et al. [7] : 800 ). Он работает с двумя отсортированными массивами A и B и записывает отсортированный вывод в массив C . Обозначение A[i...j] обозначает часть A от индекса i до j , исключая.
алгоритм merge(A[i...j], B[k...ℓ], C[p...q]) — это входные данные A, B, C : массив i, j, k, ℓ, p, q: индексы пусть m = j - i, н = ℓ - к если m < n, то поменять местами A и B // убедиться, что A — больший массив: i, j по-прежнему принадлежат A; k, ℓ — B поменять местами m и n если m ≤ 0 , то вернуть // базовый случай, объединять нечего пусть r = ⌊(i + j)/2⌋ пусть s = бинарный поиск(A[r], B[k...ℓ]) пусть t = p + (r - i) + (s - k) С[т] = А[р] параллельно делать слияние(A[i...r], B[k...s], C[p...t]) слияние(A[r+1...j], B[s...ℓ], C[t+1...q])
Алгоритм работает путем разбиения A или B , в зависимости от того, какой из них больше, на (почти) равные половины. Затем он разбивает другой массив на часть со значениями, меньшими, чем середина первой, и часть с большими или равными значениями. ( Подпрограмма двоичного поиска возвращает индекс в B , где был бы A [ r ] , если бы он был в B ; это всегда число между k и ℓ .) Наконец, каждая пара половин рекурсивно объединяется , и поскольку рекурсивные вызовы независимы друг от друга, они могут выполняться параллельно. Гибридный подход, где последовательный алгоритм используется для базового случая рекурсии, показал хорошую производительность на практике [8]
Работа , выполняемая алгоритмом для двух массивов, содержащих в общей сложности n элементов, т. е. время выполнения его последовательной версии, составляет O ( n ) . Это оптимально, поскольку n элементов необходимо скопировать в C . Чтобы вычислить охват алгоритма, необходимо вывести отношение рекуррентности . Поскольку два рекурсивных вызова merge параллельны, необходимо рассматривать только более затратный из двух вызовов. В худшем случае максимальное количество элементов в одном из рекурсивных вызовов не превышает , поскольку массив с большим количеством элементов идеально делится пополам. Добавляя стоимость двоичного поиска, мы получаем эту рекуррентность в качестве верхней границы:
Решением является , то есть это займет столько времени на идеальной машине с неограниченным числом процессоров. [7] : 801–802
Примечание: Процедура нестабильна : если равные элементы разделены путем разделения A и B , они станут чередоваться в C ; также перестановка A и B разрушит порядок, если равные элементы распределены между обоими входными массивами. В результате, при использовании для сортировки, этот алгоритм производит сортировку, которая нестабильна.
Существуют также алгоритмы, которые вводят параллелизм в рамках одного экземпляра слияния двух отсортированных списков. Они могут использоваться в программируемых пользователем вентильных матрицах ( ПЛИС ), специализированных схемах сортировки, а также в современных процессорах с однокомандными множественными данными ( SIMD ).
Существующие параллельные алгоритмы основаны на модификациях части слияния либо битонического сортировщика , либо сортировки слиянием нечетных-четных чисел . [9] В 2018 году Сайто М. и др. представили MMS [10] для ПЛИС, которая была сосредоточена на удалении многоциклового пути обратной связи, который препятствовал эффективной конвейеризации в оборудовании. Также в 2018 году Папафилиппоу П. и др. представили FLiMS [9] , которая улучшила использование оборудования и производительность, требуя только этапов конвейера блоков сравнения и обмена P/2 для слияния с параллелизмом элементов P на цикл ПЛИС.
Некоторые компьютерные языки предоставляют встроенную или библиотечную поддержку для слияния отсортированных коллекций .
В библиотеке стандартных шаблонов C++ есть функция std::merge , которая объединяет два отсортированных диапазона итераторов , и std::inplace_merge , которая объединяет два последовательных отсортированных диапазона in-place . Кроме того, класс std::list (связанный список) имеет свой собственный метод merge , который объединяет другой список в себя. Тип объединенных элементов должен поддерживать оператор "меньше" ( < ), или он должен быть снабжен пользовательским компаратором.
C++17 допускает различные политики выполнения, а именно последовательную, параллельную и параллельно-непоследовательную. [11]
Стандартная библиотека Python (начиная с версии 2.6) также имеет функцию merge в модуле heapq , которая берет несколько отсортированных итерируемых объектов и объединяет их в один итератор. [12]