
Плоскость орбиты вращающегося тела — это геометрическая плоскость , в которой лежит его орбита . Для определения плоскости орбиты достаточно трех неколлинеарных точек в пространстве. Типичным примером могут служить положения центров массивного тела (хозяина) и вращающегося небесного тела в два разных момента времени/точки его орбиты.
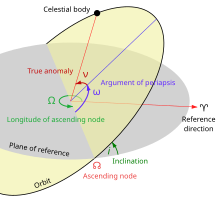
Орбитальная плоскость определяется по отношению к плоскости отсчета двумя параметрами : наклоном ( i ) и долготой восходящего узла (Ω).
По определению, плоскостью отсчета для Солнечной системы обычно считается плоскость орбиты Земли , которая определяет эклиптику — круговую траекторию на небесной сфере , по которой Солнце движется в течение года.
В других случаях, например, когда Луна или искусственный спутник вращаются вокруг другой планеты, удобно определять наклон орбиты Луны как угол между ее орбитальной плоскостью и экваториальной плоскостью планеты .
Определенная система координат, использующая в качестве плоскости орбитальную плоскость, известна как перифокальная система координат .
Для ракет-носителей и искусственных спутников плоскость орбиты является определяющим параметром орбиты; как правило, для изменения плоскости орбиты объекта потребуется очень большое количество топлива . Другие параметры, такие как период орбиты , эксцентриситет орбиты и фаза орбиты, легче изменяются с помощью двигательных систем.
Орбитальные плоскости спутников возмущаются несферической природой гравитации Земли . Это заставляет орбитальную плоскость орбиты спутника медленно вращаться вокруг Земли в зависимости от угла, который плоскость образует с экватором Земли. Для плоскостей, которые находятся под критическим углом, это может означать, что плоскость будет следовать за Солнцем вокруг Земли, образуя солнечно-синхронную орбиту .
Окно запуска ракеты-носителя обычно определяется временем пересечения плоскости целевой орбиты с местом запуска.