
.jpg/440px-Mars_-_2020_Opposition_(crop).jpg)
Марс имеет орбиту с большой полуосью 1,524 астрономических единиц (228 миллионов км) (12,673 световых минут) и эксцентриситетом 0,0934. [1] [2] Планета совершает оборот вокруг Солнца за 687 дней [3] и проходит за это время 9,55 а.е. [4] , что делает среднюю орбитальную скорость 24 км/с.
Эксцентриситет больше, чем у любой другой планеты, за исключением Меркурия, и это приводит к большой разнице между расстояниями афелия и перигелия — они составляют соответственно 1,666 и 1,381 а.е. [5]
Марс находится в середине долгосрочного увеличения эксцентриситета. Он достиг минимума в 0,079 около 19 тысяч лет назад и достигнет пика около 0,105 примерно через 24 тысячелетия с настоящего момента (и с перигелийными расстояниями всего в 1,3621 астрономических единиц ). Орбита временами близка к круговой: она была 0,002 1,35 миллиона лет назад и достигнет аналогичного минимума через 1,05 миллиона лет в будущем. [ необходимо разъяснение ] Максимальный эксцентриситет между этими двумя крайними минимумами составляет 0,12 примерно через 200 тысяч лет. [6]
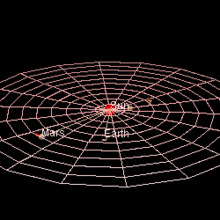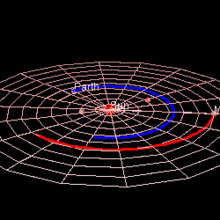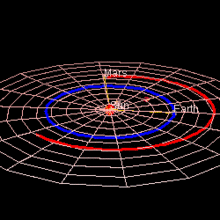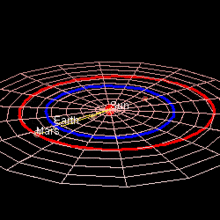
Марс достигает противостояния , когда разница между его геоцентрической долготой и Солнцем составляет 180°. В момент, близкий к противостоянию (в течение 8½ дней), расстояние между Землей и Марсом настолько мало, насколько это возможно в течение этого 780-дневного синодического периода . [7] Каждое противостояние имеет определенное значение, поскольку Марс виден с Земли всю ночь, высоко и полностью освещен, но те, которые представляют особый интерес, случаются, когда Марс находится вблизи перигелия, поскольку именно в это время Марс также находится ближе всего к Земле. За одним перигелийным противостоянием следует другое либо через 15, либо через 17 лет. Фактически за каждым противостоянием следует похожее противостояние через 7 или 8 синодических периодов, и очень похожее противостояние через 37 синодических периодов (79 лет). [8] В так называемом перигелийном противостоянии Марс находится ближе всего к Солнцу и особенно близко к Земле: противостояния варьируются от примерно 0,68 а.е., когда Марс находится вблизи афелия, до всего лишь примерно 0,37 а.е., когда Марс находится вблизи перигелия. [9]
Марс подходит к Земле ближе, чем любая другая планета, за исключением Венеры в ее самом близком — 56 миллионов км — это самое близкое расстояние между Марсом и Землей, тогда как самое близкое расстояние Венеры к Земле составляет 40 миллионов км. Марс подходит ближе всего к Земле раз в два года, примерно во время своего противостояния, когда Земля проходит между Солнцем и Марсом. Очень близкие противостояния Марса случаются каждые 15–17 лет, когда мы проходим между Марсом и Солнцем примерно во время его перигелия (ближайшей точки к Солнцу на орбите). Минимальное расстояние между Землей и Марсом сокращалось с годами, и в 2003 году минимальное расстояние составило 55,76 миллиона км, что ближе, чем любое подобное сближение за почти 60 000 лет (57 617 до н. э.). Рекордно минимальное расстояние между Землей и Марсом в 2729 году составит 55,65 миллиона км. В 3818 году рекорд составит 55,44 млн км, и расстояния будут продолжать уменьшаться в течение примерно 24 000 лет. [10]
До работы Иоганна Кеплера (1571–1630), немецкого астронома, преобладающим мнением было то, что Солнце и планеты вращаются вокруг Земли. В 1543 году Николай Коперник предположил, что все планеты вращаются по кругам вокруг Солнца, но его теория не давала удовлетворительных предсказаний и была в значительной степени проигнорирована. Когда Кеплер изучал наблюдения своего начальника Тихо Браге за положением Марса на небе в течение многих ночей, Кеплер понял, что орбита Марса не может быть окружностью. После многих лет анализа Кеплер обнаружил, что орбита Марса, вероятно, представляет собой эллипс , с Солнцем в одной из фокусных точек эллипса . Это, в свою очередь, привело к открытию Кеплером того, что все планеты вращаются вокруг Солнца по эллиптическим орбитам, с Солнцем в одной из двух фокусных точек. Это стало первым из трех законов движения планет Кеплера . [11] [12]
С точки зрения всех, кроме самых требовательных, путь Марса прост. Уравнение в Астрономических алгоритмах , которое предполагает невозмущенную эллиптическую орбиту, предсказывает время перигелия и афелия с ошибкой в «несколько часов». [13] Использование орбитальных элементов для расчета этих расстояний согласуется с фактическими средними значениями по крайней мере до пяти значащих цифр. Формулы для расчета положения напрямую из орбитальных элементов обычно не предоставляют или не требуют поправок на эффекты других планет. [14]
Для более высокого уровня точности требуются возмущения планет. Они хорошо известны и, как полагают, достаточно хорошо смоделированы для достижения высокой точности. Это все тела, которые необходимо учитывать даже для многих сложных задач. Когда Альдо Витальяно вычислял дату близких марсианских подходов в далеком прошлом или будущем, он проверил потенциальный эффект, вызванный неопределенностями моделей пояса астероидов , запустив моделирование как с тремя крупнейшими астероидами, так и без них, и обнаружил, что эффекты были незначительными.
Наблюдения улучшились, и технологии космической эры заменили старые методы. Э. Майлз Стэндиш писал: «Классические эфемериды за последние столетия были основаны исключительно на оптических наблюдениях: почти исключительно на времени прохождения меридианного круга. С появлением планетарных радаров, миссий космических аппаратов, VLBI и т. д. ситуация для четырех внутренних планет кардинально изменилась». (8.5.1 стр. 10) Для DE405, созданного в 1995 году, оптические наблюдения были прекращены, и, как он писал, «начальные условия для четырех внутренних планет были скорректированы в первую очередь с учетом данных о дальности…» [15] Известно, что ошибка в DE405 составляет около 2 км, а сейчас она составляет менее километра. [16]
Хотя возмущения на Марсе, вызванные астероидами, вызвали проблемы, они также использовались для оценки масс некоторых астероидов. [17] Однако улучшение модели пояса астероидов вызывает большую озабоченность у тех, кому требуются или кто пытается предоставить эфемериды наивысшей точности. [18]
В следующей таблице элементов орбиты Марса представлено не более пяти значимых цифр . На этом уровне точности числа очень хорошо соответствуют элементам VSOP87 и расчетам, полученным на их основе, а также 250-летнему наилучшему соответствию Стэндиша (из JPL) и расчетам с использованием фактических положений Марса с течением времени.