
В физике и материаловедении пластичность (также известная как пластическая деформация ) — это способность твердого материала подвергаться постоянной деформации , необратимому изменению формы в ответ на приложенные силы. [1] [2] Например, сплошной кусок металла, сгибаемый или расплющиваемый в новую форму , проявляет пластичность, поскольку постоянные изменения происходят внутри самого материала. В технике переход от упругого поведения к пластическому поведению известен как текучесть .
Пластическая деформация наблюдается в большинстве материалов, особенно в металлах , почвах , горных породах , бетоне и пенах . [3] [4] [5] [6] Однако физические механизмы, вызывающие пластическую деформацию, могут сильно различаться. В кристаллическом масштабе пластичность металлов обычно является следствием дислокаций . Такие дефекты относительно редки в большинстве кристаллических материалов, но многочисленны в некоторых и части их кристаллической структуры; в таких случаях может возникнуть пластическая кристалличность . В хрупких материалах, таких как горные породы, бетон и кости, пластичность обусловлена преимущественно скольжением в микротрещинах . В ячеистых материалах, таких как жидкие пены или биологические ткани , пластичность в основном является следствием перестроек пузырьков или клеток, в частности процессов T1 .
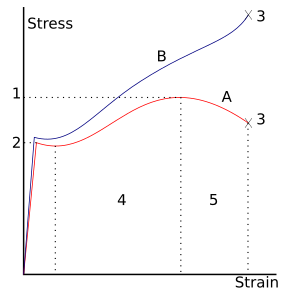
Для многих пластичных металлов растягивающая нагрузка, приложенная к образцу, заставит его вести себя упруго. Каждое увеличение нагрузки сопровождается пропорциональным увеличением удлинения. Когда нагрузка снимается, деталь возвращается к своему первоначальному размеру. Однако, как только нагрузка превышает пороговое значение – предел текучести – удлинение увеличивается быстрее, чем в упругой области; теперь, когда нагрузка снимается, некоторая степень удлинения останется.
Упругая деформация , однако, является приближением, и ее качество зависит от рассматриваемых временных рамок и скорости нагрузки. Если, как указано на графике напротив, деформация включает упругую деформацию, ее также часто называют «упруго-пластической деформацией» или «упруго-пластической деформацией».
Идеальная пластичность — это свойство материалов подвергаться необратимой деформации без увеличения напряжений или нагрузок. Пластичные материалы, которые были закалены предварительной деформацией, такой как холодная формовка , могут нуждаться во все более высоких напряжениях для дальнейшей деформации. Как правило, пластическая деформация также зависит от скорости деформации, т. е. для увеличения скорости деформации обычно приходится применять более высокие напряжения. Говорят, что такие материалы деформируются вязкопластично .
Пластичность материала прямо пропорциональна его пластичности и ковкости .

Пластичность кристалла чистого металла обусловлена в первую очередь двумя модами деформации в кристаллической решетке: скольжением и двойникованием. Скольжение — это деформация сдвига, которая перемещает атомы на многие межатомные расстояния относительно их исходных положений. Двойникование — это пластическая деформация, которая происходит вдоль двух плоскостей из-за набора сил, приложенных к данному металлическому куску.
Большинство металлов проявляют большую пластичность в горячем состоянии, чем в холодном. Свинец проявляет достаточную пластичность при комнатной температуре, в то время как чугун не обладает достаточной пластичностью для любой кузнечной операции даже в горячем состоянии. Это свойство имеет важное значение при формовании, формовании и выдавливании металлов. Большинство металлов становятся пластичными при нагревании и, следовательно, формуются в горячем состоянии.
Кристаллические материалы содержат однородные плоскости атомов, организованные с дальним порядком. Плоскости могут проскальзывать мимо друг друга вдоль своих плотно упакованных направлений, как показано на странице систем скольжения. Результатом является постоянное изменение формы внутри кристалла и пластическая деформация. Наличие дислокаций увеличивает вероятность плоскостей.
В наномасштабе первичная пластическая деформация в простых гранецентрированных кубических металлах обратима, пока нет переноса материала в форме поперечного скольжения . [7] Сплавы с эффектом памяти формы, такие как проволока из нитинола, также демонстрируют обратимую форму пластичности, которую правильнее называть псевдоупругостью .
Наличие других дефектов внутри кристалла может запутывать дислокации или иным образом препятствовать их скольжению. Когда это происходит, пластичность локализуется в определенных областях материала. Для кристаллов эти области локализованной пластичности называются полосами сдвига .
Микропластичность — локальное явление в металлах. Оно происходит при значениях напряжения , когда металл находится в глобальном упругом домене, а некоторые локальные области — в пластическом домене. [8]
В аморфных материалах обсуждение «дислокаций» неприменимо, поскольку весь материал не имеет дальнего порядка. Эти материалы все еще могут подвергаться пластической деформации. Поскольку аморфные материалы, такие как полимеры, не являются хорошо упорядоченными, они содержат большое количество свободного объема или неиспользуемого пространства. Растягивание этих материалов при растяжении открывает эти области и может придать материалам мутный вид. Эта мутность является результатом образования трещин , когда внутри материала в областях высокого гидростатического напряжения образуются фибриллы . Материал может перейти от упорядоченного вида к «сумасшедшему» узору деформации и растяжений.
Эти материалы пластически деформируются, когда изгибающий момент превышает полностью пластический момент. Это относится к пенам с открытыми ячейками, где изгибающий момент прикладывается к стенкам ячеек. Пены могут быть изготовлены из любого материала с пределом пластической текучести, включая жесткие полимеры и металлы. Этот метод моделирования пены в виде балок действителен только в том случае, если отношение плотности пены к плотности вещества меньше 0,3. Это происходит потому, что балки деформируются в осевом направлении, а не изгибаются. В пенах с закрытыми ячейками предел текучести увеличивается, если материал находится под напряжением из-за мембраны, которая охватывает поверхность ячеек.
Почвы, особенно глины, демонстрируют значительную неэластичность под нагрузкой. Причины пластичности почв могут быть довольно сложными и сильно зависеть от микроструктуры , химического состава и содержания воды. Пластичное поведение почв обусловлено в первую очередь перестройкой кластеров соседних зерен.
Неупругие деформации горных пород и бетона в первую очередь обусловлены образованием микротрещин и скользящими движениями относительно этих трещин. При высоких температурах и давлениях на пластическое поведение может также влиять движение дислокаций в отдельных зернах микроструктуры.
[9]
Не зависящее от времени пластическое течение как в монокристаллах, так и в поликристаллах определяется критическим/максимальным разрешенным напряжением сдвига ( τ CRSS ), инициирующим миграцию дислокаций вдоль параллельных плоскостей скольжения единой системы скольжения, тем самым определяя переход от упругого к пластическому деформационному поведению в кристаллических материалах.
Критическое разрешенное напряжение сдвига для монокристаллов определяется законом Шмида τ CRSS =σ y /m, где σ y — предел текучести монокристалла, а m — фактор Шмида. Фактор Шмида состоит из двух переменных λ и φ, определяющих угол между направлением плоскости скольжения и приложенной силой растяжения, а также угол между нормалью плоскости скольжения и приложенной силой растяжения, соответственно. Примечательно, что поскольку m > 1, σ y > τ CRSS .
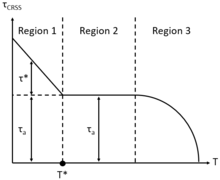
Существуют три характерные области критического разрешенного напряжения сдвига как функции температуры. В области низких температур 1 ( T ≤ 0,25 T· m ) скорость деформации должна быть высокой для достижения высокого τ CRSS , которое требуется для инициирования скольжения дислокаций и, эквивалентно, пластического течения. В области 1 критическое разрешенное напряжение сдвига имеет две компоненты: атермическое ( τ a ) и термическое ( τ *) напряжения сдвига, возникающие из-за напряжения, необходимого для перемещения дислокаций в присутствии других дислокаций, и сопротивления препятствий точечных дефектов миграции дислокаций соответственно. При T = T * определяется умеренная температурная область 2 (0,25 T· m < T < 0,7 T· m ), где тепловой компонент напряжения сдвига τ * → 0, представляющий собой устранение сопротивления точечных дефектов миграции дислокаций. Таким образом, не зависящее от температуры критическое разрешенное напряжение сдвига τ CRSS = τ a остается таковым до тех пор, пока не будет определена область 3. Примечательно, что в области 2 следует учитывать механизмы пластической деформации (ползучести) при умеренной температуре, зависящие от времени, такие как торможение растворенным веществом. Кроме того, в области 3 с высокой температурой ( T ≥ 0,7 T m ) έ может быть низким, что способствует низкому τ CRSS , однако пластическое течение все равно будет происходить из-за термически активированных механизмов пластической деформации при высокой температуре, зависящих от времени, таких как диффузионный поток Набарро-Херринга (NH) и Кобла через решетку и вдоль поверхностей монокристаллов соответственно, а также ползучесть с переползанием-скольжением дислокаций.

На стадии легкого скольжения 1 скорость упрочнения, определяемая изменением напряжения сдвига относительно деформации сдвига ( dτ / dγ ), низкая, что соответствует небольшому количеству приложенного напряжения сдвига, необходимого для создания большого количества деформации сдвига. Легкое скольжение дислокаций и соответствующее течение объясняется миграцией дислокаций только вдоль параллельных плоскостей скольжения (т. е. одной системы скольжения). Умеренное сопротивление миграции дислокаций вдоль параллельных плоскостей скольжения проявляется в соответствии со слабыми взаимодействиями полей напряжений между этими дислокациями, которые усиливаются с уменьшением межплоскостного расстояния. В целом, эти мигрирующие дислокации в пределах одной системы скольжения действуют как слабые препятствия для течения, и наблюдается скромное повышение напряжения по сравнению с пределом текучести. На стадии линейного упрочнения 2 течения скорость упрочнения становится высокой, поскольку требуется значительное напряжение для преодоления взаимодействий полей напряжений дислокаций, мигрирующих по непараллельным плоскостям скольжения (т. е. множественным системам скольжения), действующих как сильные препятствия для течения. Для обеспечения непрерывной миграции дислокаций при малых деформациях требуется большое напряжение. Напряжение сдвигового течения прямо пропорционально квадратному корню из плотности дислокаций (τ flow ~ ρ ½ ), независимо от эволюции конфигураций дислокаций, что показывает зависимость упрочнения от количества присутствующих дислокаций. Что касается этой эволюции конфигураций дислокаций, при малых деформациях расположение дислокаций представляет собой случайный трехмерный массив пересекающихся линий. Умеренные деформации соответствуют ячеистым дислокационным структурам с неоднородным распределением дислокаций с большой плотностью дислокаций на границах ячеек и малой плотностью дислокаций внутри ячеек. При еще больших деформациях ячеистая дислокационная структура уменьшается в размерах до тех пор, пока не будет достигнут минимальный размер. Наконец, скорость упрочнения при обработке снова становится низкой на стадии истощения/насыщения упрочнения 3 пластического течения, поскольку малые напряжения сдвига вызывают большие деформации сдвига. В частности, в случаях, когда множественные системы скольжения ориентированы благоприятно по отношению к приложенному напряжению, τ CRSS для этих систем может быть схожим, и текучесть может происходить в соответствии с миграцией дислокаций вдоль множественных систем скольжения с непараллельными плоскостями скольжения, демонстрируя скорость упрочнения стадии 1, типичную для стадии 2. Наконец, ниже суммируется различие между не зависящей от времени пластической деформацией в объемно-центрированных кубических переходных металлах и гранецентрированных кубических металлах.
Пластичность поликристаллов существенно отличается от пластичности монокристаллов из-за наличия дефектов на границах зерен (ГЗ), которые действуют как очень сильные препятствия для пластического течения, затрудняя миграцию дислокаций по всей длине активированной плоскости(ей) скольжения. Следовательно, дислокации не могут переходить из одного зерна в другое через границу зерна. В следующих разделах рассматриваются конкретные требования ГЗ для обширной пластической деформации поликристаллов перед разрушением, а также влияние микроскопической текучести внутри отдельных кристаллитов на макроскопическую текучесть поликристалла. Критическое разрешенное напряжение сдвига для поликристаллов также определяется законом Шмида (τ CRSS =σ y /ṁ), где σ y — предел текучести поликристалла, а ṁ — взвешенный фактор Шмида. Взвешенный фактор Шмида отражает наименее благоприятно ориентированную систему скольжения среди наиболее благоприятно ориентированных систем скольжения зерен, составляющих ГЗ.
Ограничение GB для поликристаллов можно объяснить, рассмотрев границу зерен в плоскости xz между двумя монокристаллами A и B одинакового состава, структуры и систем скольжения, но разориентированными относительно друг друга. Чтобы гарантировать, что пустоты не образуются между индивидуально деформирующимися зернами, ограничение GB для бикристалла выглядит следующим образом: ε xx A = ε xx B (x-осевая деформация в GB должна быть эквивалентна для A и B), ε zz A = ε zz B (z-осевая деформация в GB должна быть эквивалентна для A и B) и ε xz A = ε xz B (xz-сдвиговая деформация вдоль плоскости xz-GB должна быть эквивалентна для A и B). Кроме того, это ограничение GB требует, чтобы на кристаллит, составляющий GB, были активированы пять независимых систем скольжения. Примечательно, что поскольку независимые системы скольжения определяются как плоскости скольжения, на которых миграции дислокаций не могут быть воспроизведены никакой комбинацией миграций дислокаций вдоль плоскостей других систем скольжения, число геометрических систем скольжения для данной кристаллической системы, которая по определению может быть построена комбинациями систем скольжения, обычно больше, чем число независимых систем скольжения. Примечательно, что существует максимум пять независимых систем скольжения для каждой из семи кристаллических систем, однако не все семь кристаллических систем достигают этого верхнего предела. Фактически, даже в пределах данной кристаллической системы состав и решетка Браве диверсифицируют число независимых систем скольжения (см. таблицу ниже). В случаях, когда кристаллиты поликристалла не получают пять независимых систем скольжения, условие GB не может быть выполнено, и, таким образом, независимая от времени деформация отдельных кристаллитов приводит к трещинам и пустотам в границах GB поликристалла, и вскоре реализуется разрушение. Следовательно, при заданном составе и структуре монокристалл с менее чем пятью независимыми системами скольжения прочнее (обладает большей степенью пластичности), чем его поликристаллическая форма.
Хотя два кристаллита A и B, обсуждавшиеся в предыдущем разделе, имеют идентичные системы скольжения, они разориентированы относительно друг друга и, следовательно, разориентированы относительно приложенной силы. Таким образом, микроскопическая текучесть внутри кристаллита может происходить в соответствии с правилами, регулирующими независимую от времени текучесть монокристалла. В конечном итоге активированные плоскости скольжения внутри зерен позволят дислокациям мигрировать в ГЗ, где затем многие дислокации накапливаются как геометрически необходимые дислокации. Это накопление соответствует градиентам деформации по отдельным зернам, поскольку плотность дислокаций вблизи ГЗ больше, чем внутри зерна, что создает напряжение на соседнем зерне в контакте. При рассмотрении бикристалла AB в целом наиболее благоприятно ориентированная система скольжения в A не будет той, что в B, и, следовательно, τ A CRSS ≠ τ B CRSS . Первостепенным является тот факт, что макроскопическая текучесть бикристалла продлевается до тех пор, пока не будет достигнуто более высокое значение τ CRSS между зернами A и B в соответствии с ограничением GB. Таким образом, для данного состава и структуры поликристалл с пятью независимыми системами скольжения прочнее (большая степень пластичности), чем его монокристаллическая форма. Соответственно, скорость упрочнения будет выше для поликристалла, чем для монокристалла, поскольку для создания деформаций требуется большее напряжение в поликристалле. Важно, что, как и в случае с напряжением течения монокристалла, τ flow ~ρ ½ , но также обратно пропорционально квадратному корню из среднего диаметра зерна (τ flow ~d -½ ). Следовательно, напряжение течения поликристалла, а следовательно, и прочность поликристалла, увеличиваются с малым размером зерна. Причина этого в том, что более мелкие зерна имеют относительно меньшее количество плоскостей скольжения, которые необходимо активировать, что соответствует меньшему количеству дислокаций, мигрирующих в ГЗ, и, следовательно, меньшему напряжению, наведенному на соседние зерна из-за скопления дислокаций. Кроме того, для заданного объема поликристалла более мелкие зерна представляют собой более прочные границы зерен-препятствий. Эти два фактора дают понимание того, почему начало макроскопического течения в мелкозернистых поликристаллах происходит при больших приложенных напряжениях, чем в крупнозернистых поликристаллах.

Существует несколько математических описаний пластичности. [12] Одной из них является теория деформации (см., например, закон Гука ), где тензор напряжения Коши (порядка d-1 в d измерениях) является функцией тензора деформации. Хотя это описание является точным, когда небольшая часть вещества подвергается возрастающей нагрузке (такой как деформационная нагрузка), эта теория не может объяснить необратимость.
Пластичные материалы могут выдерживать большие пластические деформации без разрушения . Однако даже пластичные металлы будут разрушаться, когда деформация станет достаточно большой — это происходит в результате упрочнения материала, что делает его хрупким . Термическая обработка, такая как отжиг , может восстановить пластичность обработанной детали, так что формование может продолжаться.
В 1934 году Эгон Орован , Майкл Полани и Джеффри Ингрэм Тейлор примерно одновременно поняли, что пластическую деформацию пластичных материалов можно объяснить с помощью теории дислокаций . Математическая теория пластичности, теория пластичности течения , использует набор нелинейных, неинтегрируемых уравнений для описания набора изменений деформации и напряжения по отношению к предыдущему состоянию и небольшому увеличению деформации.

Если напряжение превышает критическое значение, как было упомянуто выше, материал подвергнется пластической или необратимой деформации. Это критическое напряжение может быть растягивающим или сжимающим. Критерии Трески и фон Мизеса обычно используются для определения того, достиг ли материал текучести. Однако эти критерии оказались недостаточными для большого диапазона материалов, и несколько других критериев текучести также широко используются.
Критерий Треска основан на представлении о том, что когда материал разрушается, он делает это при сдвиге, что является относительно хорошим предположением при рассмотрении металлов. Учитывая основное напряженное состояние, мы можем использовать круг Мора для решения максимальных касательных напряжений, которые испытает наш материал, и сделать вывод, что материал разрушится, если
где σ 1 — максимальное нормальное напряжение, σ 3 — минимальное нормальное напряжение, а σ 0 — напряжение, при котором материал разрушается при одноосной нагрузке. Можно построить поверхность текучести , которая дает визуальное представление этой концепции. Внутри поверхности текучести деформация упругая. На поверхности деформация пластическая. Материал не может иметь напряженные состояния вне своей поверхности текучести.
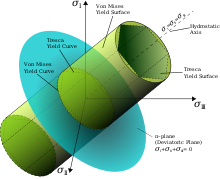
Критерий Хубера–фон Мизеса [13] основан на критерии Трески, но учитывает предположение, что гидростатические напряжения не способствуют разрушению материала. М. Т. Хубер был первым, кто предложил критерий энергии сдвига. [14] [15] Фон Мизес решает для эффективного напряжения при одноосной нагрузке, вычитая гидростатические напряжения, и утверждает, что все эффективные напряжения, большие, чем то, которое вызывает разрушение материала при одноосной нагрузке, приведут к пластической деформации.
Опять же, визуальное представление поверхности текучести может быть построено с использованием приведенного выше уравнения, которое принимает форму эллипса. Внутри поверхности материалы подвергаются упругой деформации. Достижение поверхности означает, что материал подвергается пластической деформации.
{{cite book}}: CS1 maint: location missing publisher (link)