В теоретической физике предпочтительная или привилегированная система отсчета — это обычно особая гипотетическая система отсчета , в которой законы физики могут казаться заметно отличающимися (более простыми) от законов в других системах отсчета.
В теориях, которые применяют принцип относительности к инерциальному движению, физика одинакова во всех инерциальных системах отсчета и даже одинакова во всех системах отсчета, подчиняющихся принципу общей теории относительности .
В теориях, предполагающих, что свет движется с фиксированной скоростью относительно неизменяемого и обнаруживаемого светоносного эфира , предпочтительной системой отсчета будет система, в которой этот эфир будет неподвижен. В 1887 году Майкельсон и Морли попытались определить состояние движения эфира. Для этого они предположили, что относительность Галилея удовлетворяется часами и линейками; то есть, что длина линеек и периоды часов инвариантны при любом изменении системы отсчета Галилея. Согласно такой гипотезе, эфир должен был наблюдаться.
Сравнивая измерения, сделанные в разных направлениях, и ища эффект, вызванный орбитальной скоростью Земли, их эксперимент, как известно, дал нулевой результат . Как следствие, в теории эфира Лоренца преобразование Галилея было заменено преобразованием Лоренца . Однако в теории эфира Лоренца предполагается существование необнаруживаемого эфира, и принцип относительности выполняется. Теория была быстро заменена специальной теорией относительности , которая дала похожие формулы без существования ненаблюдаемого эфира. Все инерциальные системы физически эквивалентны в обеих теориях. Точнее, при условии, что никакое явление не нарушает принцип относительности движения, нет никаких средств для измерения скорости инерциального наблюдателя относительно возможной среды распространения квантовых волн.
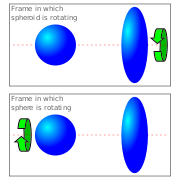
Хотя все инерциальные системы эквивалентны в классической механике и специальной теории относительности , набор всех инерциальных систем имеет привилегии по сравнению с неинерциальными системами в этих теориях. [1] : 10 Инерциальные системы имеют привилегии, потому что они не имеют физики, причины которой находятся вне системы, в то время как неинерциальные системы имеют. Эйнштейн приводит следующий пример: предположим, что два одинаково составленных упругих тела находятся в пространстве и удалены друг от друга так, что взаимодействие между ними можно игнорировать, и единственным относительным движением которых является равномерное жесткое вращение вокруг линии, соединяющей центры обоих тел (подобно вращающимся колесам вокруг оси ) . Одно из тел является сферой , а другое — сфероидом , сплющенной сферой. Наблюдаемая собственная физическая форма тел остается одинаковой во всех системах. Система невращающегося сфероида имеет физику, причина которой лежит вне системы, отвечая за сплющенность сфероида. Система отсчета невращающейся сферы не имеет, что делает ее привилегированной, поскольку она не требует внешних причин. Это относится ко всем инерциальным системам отсчета, которые являются привилегированными в том же отношении. [1] : 209 Эйнштейн продолжил развивать общую теорию относительности и принцип эквивалентности , в котором инерциально-гравитационные системы отсчета больше не являются привилегированными, [1] : 215–223 потому что геодезические пространства - времени объясняют эти инерциально-гравитационные эффекты без внешней причины. [2]