График Q–Q

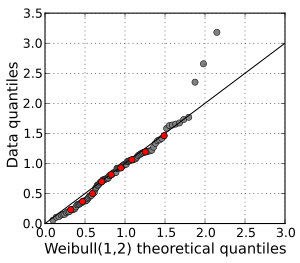
В статистике график Q–Q ( график квантиля–квантиля ) — это вероятностный график, графический метод сравнения двух распределений вероятностей путем построения их квантилей друг против друга. ^[1] Точка $(x, y)$ на графике соответствует одному из квантилей второго распределения ( координата $y$ ), построенному относительно того же квантиля первого распределения ( координата $x$ ). Это определяет параметрическую кривую , где параметром является индекс квантильного интервала.

Если два сравниваемых распределения подобны, точки на графике Q–Q будут приблизительно лежать на линии тождества $y = x$ . Если распределения линейно связаны, точки на графике Q–Q будут приблизительно лежать на линии, но не обязательно на линии $y = x$ . Графики Q–Q также можно использовать в качестве графического средства оценки параметров в семействе распределений в масштабе местоположения .

График AQ–Q используется для сравнения форм распределений, предоставляя графическое представление того, как такие свойства, как местоположение , масштаб и асимметрия , схожи или различны в двух распределениях. Графики Q–Q можно использовать для сравнения наборов данных или теоретических распределений . Использование графиков Q–Q для сравнения двух выборок данных можно рассматривать как непараметрический подход к сравнению их базовых распределений. График AQ–Q, как правило, более информативен, чем сравнение гистограмм выборок , но менее широко известен. Графики Q–Q обычно используются для сравнения набора данных с теоретической моделью. ^[2]^[3] Это может обеспечить оценку соответствия , которая является графической, а не сводится к числовой сводной статистике . Графики Q–Q также используются для сравнения двух теоретических распределений друг с другом. ^[4] Поскольку графики Q–Q сравнивают распределения, нет необходимости в том, чтобы значения наблюдались парами, как на графике рассеяния , или даже в том, чтобы количество значений в двух сравниваемых группах было одинаковым.

Термин «график вероятности» иногда относится конкретно к графику Q–Q, иногда к более общему классу графиков, а иногда к менее часто используемому графику P–P . График коэффициента корреляции графика вероятности (график PPCC) — это величина, полученная из идеи графиков Q–Q, которая измеряет согласие подобранного распределения с наблюдаемыми данными и которая иногда используется как средство подгонки распределения к данным.

Определение и построение

График Q–Q — это график квантилей двух распределений друг против друга или график, основанный на оценках квантилей. Схема точек на графике используется для сравнения двух распределений.

Основным шагом в построении графика Q–Q является вычисление или оценка квантилей для построения графика. Если одна или обе оси на графике Q–Q основаны на теоретическом распределении с непрерывной кумулятивной функцией распределения (CDF), все квантили однозначно определены и могут быть получены путем инвертирования CDF. Если теоретическое распределение вероятностей с прерывистой CDF является одним из двух сравниваемых распределений, некоторые квантили могут быть не определены, поэтому может быть построен интерполированный квантиль. Если график Q–Q основан на данных, используются несколько оценщиков квантилей. Правила формирования графиков Q–Q, когда квантили должны быть оценены или интерполированы, называются позициями построения.

Простой случай — когда есть два набора данных одинакового размера. В этом случае, чтобы построить график Q–Q, нужно упорядочить каждый набор в порядке возрастания, затем разбить на пары и построить соответствующие значения. Более сложная конструкция — случай, когда сравниваются два набора данных разного размера. Чтобы построить график Q–Q в этом случае, необходимо использовать интерполированную оценку квантиля, чтобы можно было построить квантили, соответствующие одной и той же базовой вероятности.

Более абстрактно, ^[4] при наличии двух кумулятивных функций распределения вероятностей $F$ и $G$ с соответствующими функциями квантилей $F -1$ и $G -1$ (обратная функция CDF является функцией квантиля), график Q–Q рисует $q$ -й квантиль $F$ против $q$ -го квантиля $G$ для диапазона значений $q$ . Таким образом, график Q–Q представляет собой параметрическую кривую , индексированную на [0,1] со значениями в действительной плоскости $R 2$ .

Интерпретация

Точки, нанесенные на график Q–Q, всегда не убывают, если смотреть слева направо. Если два сравниваемых распределения идентичны, график Q–Q следует линии 45° $y = x$ . Если два распределения согласуются после линейного преобразования значений в одном из распределений, то график Q–Q следует некоторой линии, но не обязательно линии $y = x$ . Если общий тренд графика Q–Q более пологий, чем линия $y = x$ , распределение, нанесенное на горизонтальную ось, более разбросано , чем распределение, нанесенное на вертикальную ось. И наоборот, если общий тренд графика Q–Q круче, чем линия $y = x$ , распределение, нанесенное на вертикальную ось, более разбросано , чем распределение, нанесенное на горизонтальную ось. Графики Q–Q часто имеют дугообразную или S-образную форму, что указывает на то, что одно из распределений более асимметрично, чем другое, или что одно из распределений имеет более тяжелые хвосты, чем другое.

Хотя график Q–Q основан на квантилях, в стандартном графике Q–Q невозможно определить, какая точка на графике Q–Q определяет данный квантиль. Например, невозможно определить медиану любого из двух сравниваемых распределений, проверив график Q–Q. Некоторые графики Q–Q указывают децили, чтобы сделать возможными такие определения.

Интерсепт и наклон линейной регрессии между квантилями дают меру относительного расположения и относительного масштаба выборок. Если медиана распределения, построенного по горизонтальной оси, равна 0, то отрезок линии регрессии является мерой расположения, а наклон — мерой масштаба. Расстояние между медианами — это еще одна мера относительного расположения, отраженная на графике Q–Q. « Коэффициент корреляции графика вероятности » (график PPCC) — это коэффициент корреляции между парными квантилями выборки. Чем ближе коэффициент корреляции к единице, тем ближе распределения к смещенным, масштабированным версиям друг друга. Для распределений с одним параметром формы график коэффициента корреляции графика вероятности предоставляет метод оценки параметра формы — просто вычисляется коэффициент корреляции для разных значений параметра формы и используется тот, который лучше всего подходит, как если бы сравнивались распределения разных типов.

Другое распространенное применение графиков Q–Q — сравнение распределения выборки с теоретическим распределением, таким как стандартное нормальное распределение $N (0,1)$ , как в нормальном вероятностном графике . Как и в случае сравнения двух выборок данных, данные упорядочиваются (формально, вычисляются порядковые статистики), затем они наносятся на график относительно определенных квантилей теоретического распределения. ^[3]

Построение позиций

Выбор квантилей из теоретического распределения может зависеть от контекста и цели. Один выбор, учитывая выборку размера $n$ , это $k / n$ для $k = 1, \dots, n$ , поскольку это квантили, которые реализует распределение выборки . Последний из них, $n / n$ , соответствует 100-му процентилю — максимальному значению теоретического распределения, которое иногда бесконечно. Другие варианты — это использование $(k - 0,5) / n$ , или вместо этого разнесение точек $n$ таким образом, чтобы между всеми ними, а также между двумя самыми внешними точками и краями интервала было равное расстояние , используя $k$ $/ ($ $n$ $+ 1)$ . ^[6] $[0,1]$

Было предложено много других вариантов, как формальных, так и эвристических, основанных на теории или моделировании, релевантном в контексте. В следующих подразделах обсуждаются некоторые из них. Более узкий вопрос — это выбор максимума (оценка максимума популяции), известный как проблема немецкого танка , для которого существуют похожие решения «максимум выборки плюс пробел», наиболее просто $m + m / n - 1.$ Более формальное применение этой униформизации интервала происходит при оценке максимального интервала параметров.

Ожидаемое значение статистики порядка для равномерного распределения

Подход $k / (n + 1)$ эквивалентен построению точек в соответствии с вероятностью того, что последнее из ( $n + 1$ ) случайно выбранных значений не превысит $k$ -го наименьшего из первых $n$ случайно выбранных значений. ^[7]^[8]

Ожидаемое значение порядковой статистики для стандартного нормального распределения

При использовании графика нормальной вероятности в качестве квантилей используются ранги — квантили ожидаемого значения порядковой статистики стандартного нормального распределения.

В более общем смысле тест Шапиро-Уилка использует ожидаемые значения порядковых статистик заданного распределения; результирующий график и линия дают обобщенную оценку наименьших квадратов для местоположения и масштаба (из пересечения и наклона подобранной линии). ^[9] Хотя это не слишком важно для нормального распределения (местоположение и масштаб оцениваются с помощью среднего значения и стандартного отклонения соответственно), это может быть полезно для многих других распределений.

Однако для этого необходимо рассчитать ожидаемые значения порядковой статистики, что может оказаться затруднительным, если распределение не является нормальным.

Медиана статистики заказа

В качестве альтернативы можно использовать оценки медианы порядковой статистики, которые можно вычислить на основе оценок медианы порядковой статистики равномерного распределения и квантильной функции распределения; это было предложено Филлибеном (1975). ^[9]

Это можно легко сделать для любого распределения, для которого можно вычислить функцию квантиля, но, наоборот, полученные оценки местоположения и масштаба больше не являются точными оценками наименьших квадратов, хотя они существенно отличаются только для малых значений $n$ .

Эвристика

Несколько различных формул были использованы или предложены в качестве аффинно -симметричных позиций построения графиков . Такие формулы имеют вид $(k - a) / (n + 1 - 2 a)$ для некоторого значения $a$ в диапазоне от 0 до 1, что дает диапазон между $k / (n + 1)$ и $(k - 1) / (n - 1)$ .

Выражения включают в себя:

$к / (п + 1)$
$(к - 0,3) / (п + 0,4)$ . ^[10]
$(k - 0,3175) / (n + 0,365)$ . ^[11]^{[примечание 1]}
$(k - 0,326) / (n + 0,348)$ . ^[12]
$(k - ⅓) / (n + ⅓)$ . ^{[примечание 2]}
$(k - 0,375) / (n + 0,25)$ . ^{[примечание 3]}
$(к - 0,4) / (п + 0,2)$ . ^[13]
$(k - 0,44) / (n + 0,12)$ . ^{[примечание 4]}
$(k - 0,5) / n$ . ^[15]
$(k - 0,567) / (n - 0,134)$ . ^[16]
$(k - 1) / (n - 1)$ . ^{[примечание 5]}

При большом размере выборки $n$ разница между этими выражениями невелика.

Оценка Филлибена

Медианы порядковой статистики являются медианами порядковых статистик распределения. Они могут быть выражены через функцию квантиля и медианы порядковой статистики для непрерывного равномерного распределения следующим образом:

N(i)=G(U(i))

где $U (i)$ — медианы статистики равномерного порядка, а $G$ — функция квантиля для желаемого распределения. Функция квантиля — это обратная функция кумулятивной функции распределения (вероятность того, что $X$ меньше или равно некоторому значению). То есть, учитывая вероятность, мы хотим получить соответствующий квантиль кумулятивной функции распределения.

Джеймс Дж. Филлибен использует следующие оценки для медиан статистики равномерного порядка: ^[17]

m(i)={\begin{cases}1-0,5^{1/n}&i=1\\\\{\dfrac {i-0,3175}{n+0,365}}&i=2,3,\ldots ,n-1\\\\0,5^{1/n}&i=n.\end{cases}}

Причиной такой оценки является то, что медианы порядковой статистики не имеют простой формы.

Программное обеспечение

Язык программирования R поставляется с функциями для построения графиков Q–Q, а именно qqnorm и qqplot из statsпакета. fastqqПакет реализует более быстрое построение графиков для большого количества точек данных.

Смотрите также

Эмпирическая функция распределения
Пробит -анализ был разработан Честером Иттнером Блиссом в 1934 году.

Примечания

^ Обратите внимание, что здесь также используется другое выражение для первой и последней точек. [1] цитирует оригинальную работу Филлибена (1975) $.$ Это выражение является оценкой медиан U $($ $k$ $)$ .
^ Простая (и легко запоминающаяся) формула для построения графиков позиций; используется в статистическом пакете BMDP .
^ Это более раннее приближение Блома (1958), и это выражение используется в MINITAB .
^ Это положение построения графика использовалось Ирвингом И. Грингортеном ^[14] для построения точек в тестах на распределение Гумбеля .
^ Использованные Филлибеном (1975), эти $точки$ построения графика равны модам U $($ $k$ $)$ .

Ссылки

Цитаты

^ Вилк, МБ; Гнанадесикан, Р. (1968), «Методы построения вероятностных графиков для анализа данных», Biometrika , 55 (1), Biometrika Trust: 1–17, doi : 10.1093/biomet/55.1.1, JSTOR 2334448, PMID 5661047.
^ Гнанадесикан (1977), стр. 199.
^ ab Thode (2002), Раздел 2.2.2, Квантиль-квантильные графики, стр. 21
^ аб Гиббонс и Чакраборти (2003), с. 144
^ "SR 20 – North Cascades Highway – История открытия и закрытия". North Cascades Passes . Департамент транспорта штата Вашингтон. Октябрь 2009 г. Получено 8 февраля 2009 г.
^ Вейбулл, Валодди (1939), «Статистическая теория прочности материалов», IVA Handlingar, Королевская шведская академия инженерных наук (151)
^ Мэдсен, Х.О. и др. (1986), Методы структурной безопасности
^ Макконен, Л. (2008), «Завершение спора о позиции построения графика», Communications in Statistics – Theory and Methods , 37 (3): 460–467, doi : 10.1080/03610920701653094, S2CID 122822135
^ ab Тестирование на нормальность, Генри К. Тоуд, CRC Press, 2002, ISBN 978-0-8247-9613-6 , стр. 31
^ Бенард, А.; Бос-Левенбах, Э.К. (сентябрь 1953 г.). «Построение графиков наблюдений на вероятностной бумаге». Statistica Neerlandica (на голландском языке). 7 : 163–173. doi :10.1111/j.1467-9574.1953.tb00821.x.
^ "1.3.3.21. Нормальный вероятностный график". itl.nist.gov . Получено 16 февраля 2022 г. .
^ Распределение свободной позиции построения графика, Юй и Хуан
^ Каннейн (1978).
^ Грингортен, Ирвинг И. (1963). «Правило построения графика для экстремальной вероятностной статьи». Журнал геофизических исследований . 68 (3): 813–814. Bibcode : 1963JGR....68..813G. doi : 10.1029/JZ068i003p00813. ISSN 2156-2202.
↑ Хазен, Аллен (1914), «Хранение должно быть обеспечено в водохранилищах для муниципального водоснабжения», Труды Американского общества инженеров-строителей (77): 1547–1550
^ Ларсен, Каррен и Хант (1980).
^ Филлибен (1975).

Источники

В статье использованы материалы, являющиеся общественным достоянием Национального института стандартов и технологий.
Блом, Г. (1958), Статистические оценки и преобразованные бета-переменные , Нью-Йорк: John Wiley and Sons
Чемберс, Джон; Кливленд, Уильям; Кляйнер, Бит; Тьюки, Пол (1983), Графические методы анализа данных , Уодсворт
Кливленд, WS (1994) Элементы графического представления данных , Hobart Press ISBN 0-9634884-1-4
Филлибен, Дж. Дж. (февраль 1975 г.), «Тест коэффициента корреляции вероятностного графика на нормальность», Технометрика , 17 (1), Американское общество качества: 111–117, doi : 10.2307/1268008, JSTOR 1268008.
Гиббонс, Джин Дикинсон ; Чакраборти, Субхабрата (2003), Непараметрический статистический вывод (4-е изд.), CRC Press, ISBN 978-0-8247-4052-8
Гнанадесикан, Р. (1977). Методы статистического анализа многомерных наблюдений . Wiley. ISBN 0-471-30845-5.
Тоуд, Генри К. (2002), Тестирование на нормальность , Нью-Йорк: Марсель Деккер, ISBN 0-8247-9613-6

Внешние ссылки

На Викискладе есть медиафайлы по теме QQ plot .

Вероятностный график