Причинно-следственная нотация

Обозначение для выражения причины и следствия

Причинно-следственная запись — это запись, используемая для выражения причины и следствия.

В природе и человеческом обществе многие явления имеют причинно-следственные связи, где одно явление A (причина) влияет на другое явление B (следствие). Установление причинно-следственных связей является целью многих научных исследований в различных областях, от биологии ^[1] и физики ^[2] до социальных наук и экономики . ^[3] Это также предмет анализа несчастных случаев ^[4] и может считаться предпосылкой для эффективной разработки политики.

Для описания причинно-следственных связей между явлениями распространены неколичественные визуальные обозначения, такие как стрелки, например, в цикле азота или во многих учебниках по химии ^{[5] [6]} и математике ^[7] . Также используются математические соглашения, такие как нанесение независимой переменной на горизонтальную ось, а зависимой переменной на вертикальную ось ^[8] или обозначение , обозначающее, что величина " " является зависимой переменной, которая является функцией независимой переменной " ". ^[9] Причинно-следственные связи также описываются с помощью количественных математических выражений. ^[10] (См. раздел Обозначения.) ${\displaystyle y=f(x)}$ ${\displaystyle y}$ ${\displaystyle x}$

Следующие примеры иллюстрируют различные типы причинно-следственных связей. За ними следуют различные обозначения, используемые для представления причинно-следственных связей.

Примеры

Дальнейшее не обязательно предполагает соглашение, согласно которому обозначает независимую переменную, а обозначает функцию независимой переменной . Вместо этого и обозначают две величины с априори неизвестной причинно-следственной связью, которые могут быть связаны математическим выражением. ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle f(y)}$

Пример экосистемы: корреляция без причинно-следственной связи

Представьте себе количество дней с температурой ниже одного градуса по Цельсию, , вызывающее образование льда на озере, , и это заставляет медведей впадать в спячку . Хотя не вызывает и наоборот, можно написать уравнение, связывающее и . Это уравнение можно использовать для успешного расчета количества медведей в спячке , учитывая площадь поверхности озера, покрытую льдом. Однако растапливание льда в районе озера путем высыпания на него соли не заставит медведей выйти из спячки. Также пробуждение медведей путем физического потревоживания не приведет к таянию льда. В этом случае обе величины и вызваны смешивающей переменной (температурой наружного воздуха), но не друг другом. и связаны корреляцией без причинно-следственной связи. ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle y}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$

Физический пример: однонаправленная причинно-следственная связь

Предположим, что идеальная система на солнечной энергии построена таким образом, что если солнечно и солнце обеспечивает интенсивность ватт , падающих на солнечную панель m в течение секунд, электродвигатель поднимает камень весом кг на метры, . В более общем смысле мы предполагаем, что система описывается следующим выражением: ${\displaystyle I}$ ${\displaystyle 100}$ ${\displaystyle 1}$ ${\displaystyle ^{2}}$ ${\displaystyle 10~}$ ${\displaystyle 2}$ ${\displaystyle 50}$ ${\displaystyle h(I)}$

${\displaystyle I\times A\times t=m\times g\times h~}$,

где представляет собой интенсивность солнечного света (Дж· с· м ), - площадь поверхности солнечной панели (м2 ), - время (с), - масса (кг), - ускорение под действием силы тяжести Земли ( м ·с ), - высота, на которую поднимается камень (м). ${\displaystyle I}$ ${\displaystyle \cdot }$ ${\displaystyle ^{-1}}$ ${\displaystyle \cdot }$ ${\displaystyle ^{-2}}$ ${\displaystyle A}$ ${\displaystyle ^{2}}$ ${\displaystyle t}$ ${\displaystyle m}$ ${\displaystyle g}$ ${\displaystyle 9.8}$ ${\displaystyle \cdot }$ ${\displaystyle ^{-2}}$ ${\displaystyle h}$

В этом примере тот факт, что солнечно и есть интенсивность света , заставляет камень подниматься , а не наоборот; подъем камня (увеличение ) не приведет к включению солнца для освещения солнечной панели (увеличение ). Причинно-следственная связь между и однонаправленная. ${\displaystyle I}$ ${\displaystyle h(I)}$ ${\displaystyle h(I)}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle h(I)}$

Пример из медицины: две причины одного результата

Курение , и воздействие асбеста, , являются известными причинами рака, . Можно написать уравнение, описывающее эквивалентную канцерогенность между тем, сколько сигарет выкуривает человек, , и тем, сколько граммов асбеста он вдыхает, . Здесь нет ни причин , ни причин , но они оба имеют общий результат. ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle y}$ ${\displaystyle f(y)=g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$ ${\displaystyle g(y)}$ ${\displaystyle g(y)}$ ${\displaystyle f(y)}$

Пример бартера: двунаправленная причинно-следственная связь

Рассмотрим экономику, основанную на бартере, где количество коров, которыми владеет человек, имеет стоимость, измеряемую в стандартной валюте кур, . Кроме того, количество баррелей нефти, которыми владеет человек, имеет стоимость, которую можно измерить в курах, . Если существует рынок, где коров можно обменять на кур, которые, в свою очередь, могут быть обменены на баррели нефти, можно написать уравнение, описывающее соотношение стоимости между коровами и баррелями нефти . Предположим, что человек в этой экономике всегда хранит половину своей стоимости в форме коров, а другую половину в форме баррелей нефти. Тогда увеличение количества коров путем предложения им 4 коров в конечном итоге приведет к увеличению количества баррелей нефти , или наоборот. В этом случае математическое равенство описывает двунаправленную причинно-следственную связь. ${\displaystyle C}$ ${\displaystyle y}$ ${\displaystyle B}$ ${\displaystyle y}$ ${\displaystyle C(y)=B(y)}$ ${\displaystyle C}$ ${\displaystyle B}$ ${\displaystyle C(y)}$ ${\displaystyle B(y)}$ ${\displaystyle C(y)=B(y)}$

Обозначения

Химические реакции

В химии многие химические реакции обратимы и описываются с помощью уравнений, которые стремятся к динамическому химическому равновесию . В этих реакциях добавление реагента или продукта приводит к тому, что реакция происходит, производя больше продукта или больше реагента соответственно. Стандартно рисовать стрелки типа «гарпуна» вместо знака равенства, ⇌, чтобы обозначить обратимый характер реакции и динамическую причинно-следственную связь между реагентами и продуктами. ^{[5] [6]}

Статистика: Делаем нотацию

Do-calculus , и в частности оператор do, используется для описания причинно-следственных связей на языке вероятности. Обозначение, используемое в do-calculus, например: ^[11]

${\displaystyle P(Y|do(X))=P(Y)~}$,

что можно прочитать как: «вероятность того , что вы делаете ». Выражение выше описывает случай, когда не зависит от чего-либо, сделанного для . ^[10] Оно указывает, что не существует однонаправленной причинно-следственной связи, когда вызывает . ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$

Причинно-следственные диаграммы

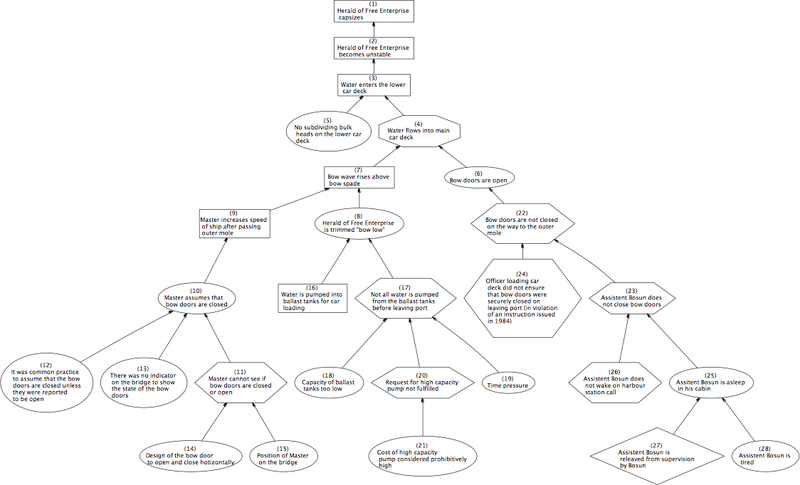
Причинно-следственная диаграмма состоит из набора узлов, которые могут быть связаны или не связаны стрелками. Стрелки между узлами обозначают причинно-следственные связи, при этом стрелка указывает от причины к следствию. Существует несколько форм причинно-следственных диаграмм, включая диаграммы Ишикавы , направленные ациклические графы , диаграммы причинно-следственных циклов ^[10] и графы «почему-потому» (WBG). На изображении ниже показан частичный граф «почему-потому» , используемый для анализа опрокидывания « Вестника свободного предпринимательства» .

Частичный график «почему–потому что» опрокидывания «Вестника свободного предпринимательства»

Модели соединений

Шаблоны соединений могут быть использованы для описания структуры графа байесовских сетей. Три возможных шаблона, разрешенных в 3-узловом направленном ациклическом графе (DAG), включают:

Обозначение причинно-следственного равенства

Существуют различные формы причинно-следственных связей. Например, две величины и могут быть вызваны вмешивающейся переменной , но не друг другом. Представьте себе забастовку мусорщиков в большом городе, , вызывает усиление запаха мусора и увеличение популяции крыс . Даже если не вызывает и наоборот, можно написать уравнение, связывающее и . Следующая таблица содержит обозначения, представляющие различные способы, которыми , и могут быть связаны друг с другом. ^[12] ${\displaystyle a(s)}$ ${\displaystyle b(s)}$ ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle a(s)}$ ${\displaystyle b(s)}$ ${\displaystyle b(s)}$ ${\displaystyle a(s)}$ ${\displaystyle b(s)}$ ${\displaystyle a(s)}$ ${\displaystyle s}$ ${\displaystyle a(s)}$ ${\displaystyle b(s)}$

Следует предположить, что связь между двумя уравнениями с идентичными смыслами причинности (такими как , и ) является чистой корреляцией, если только не доказано, что оба выражения являются двунаправленными причинно-следственными равенствами. В этом случае общая причинно-следственная связь между и является двунаправленно причинной. ${\displaystyle s~{\overset {\rightarrow }{=}}~a\left(s\right)}$ ${\displaystyle s~{\overset {\rightarrow }{=}}~b\left(s\right)}$ ${\displaystyle b(s)}$ ${\displaystyle a(s)}$

Ссылки

1. Маршалл, Барри Дж.; Уоррен, Дж. Робин (июнь 1984 г.). «Неопознанные изогнутые бациллы в желудке пациентов с гастритом и пептической язвой». The Lancet . 323 (8390): 1311–1315. doi :10.1016/S0140-6736(84)91816-6. PMID  6145023. S2CID  10066001.
2. Аспект, Ален; Гранжье, Филипп; Роджер, Жерар (12 июля 1982 г.). «Экспериментальная реализация мысленного эксперимента Эйнштейна-Подольского-Розена-Бома: новое нарушение неравенств Белла». Physical Review Letters . 49 (2): 91–94. Bibcode : 1982PhRvL..49...91A. doi : 10.1103/PhysRevLett.49.91 .
3. Фишер, Стэнли; Истерли, Уильям (1990). «Экономика ограничений государственного бюджета». The World Bank Research Observer . 5 (2): 127–142. CiteSeerX 10.1.1.1009.4220 . doi :10.1093/wbro/5.2.127. 
4. Ladkin, Peter; Loer, Karsten (апрель 1998 г.). Анализ авиационных происшествий с использованием WB-анализа — применение мультимодального рассуждения (PDF) . Весенний симпозиум. Ассоциация по развитию искусственного интеллекта . Архивировано из оригинала (PDF) 21.12.2022.
5. Bruice, Paula Yurkanis (2007). Органическая химия (5-е изд.). Pearson Prentice Hall Upper Saddle River, NJ. стр. 44,45. ISBN 978-0-13-196316-0.
6. Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey; Madura, Jeffry D. (2007). Общие принципы химии и современные приложения (9-е изд.). Pearson Prentice Hall Upper Saddle River, NJ. стр. 573–650. ISBN 978-0-13-149330-8.
7. Б. Джордж, Джордж (2007). Исчисление Томаса (11-е изд.). Пирсон. стр. 20. ISBN 978-0-321-18558-7.
8. Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри; Мадура, Джеффри Д. (2007). Общие принципы химии и современные приложения (9-е изд.). Pearson Prentice Hall Upper Saddle River, NJ. стр. 575. ISBN 978-0-13-149330-8.
9. Б. Джордж, Джордж (2007). Исчисление Томаса (11-е изд.). Пирсон. стр. 19. ISBN 978-0-321-18558-7.
10. Pearl, Judea ; Mackenzie, Dana (2018-05-15). Книга «Почему?»: Новая наука о причине и следствии. Базовые книги. ISBN 9780465097616.
11. {{Хичкок, Кристофер, «Причинные модели», Стэнфордская энциклопедия философии (издание весны 2023 г.), Эдвард Н. Залта и Ури Нодельман (ред.), URL = <https://plato.stanford.edu/archives/spr2023/entries/causal-models/>}}
12. Ван Хорн Н. и Мукерджи М. Улучшенное описание захваченных ионов как модульной электромеханической системы, J. Appl. Phys. 135, 154401 (2024)