
Моделирование структурных уравнений ( SEM ) — это разнообразный набор методов, используемых учеными, проводящими как наблюдательные, так и экспериментальные исследования. SEM в основном используется в социальных и поведенческих науках, но также применяется в эпидемиологии, [2] бизнесе, [3] и других областях. Определение SEM сложно дать без ссылки на технический язык, но хорошей отправной точкой является само название.
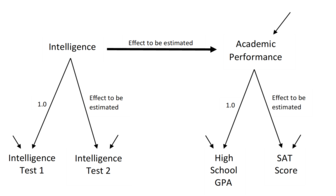
SEM включает модель, представляющую, как различные аспекты некоторого явления , как предполагается, причинно связаны друг с другом. Модели структурных уравнений часто содержат постулированные причинные связи между некоторыми скрытыми переменными (переменными, которые, как предполагается, существуют, но которые не могут наблюдаться напрямую). Дополнительные причинные связи связывают эти скрытые переменные с наблюдаемыми переменными, значения которых появляются в наборе данных. Причинные связи представлены с помощью уравнений , но постулируемая структуризация также может быть представлена с помощью диаграмм, содержащих стрелки, как на рисунках 1 и 2. Причинные структуры подразумевают, что определенные закономерности должны появляться среди значений наблюдаемых переменных. Это позволяет использовать связи между значениями наблюдаемых переменных для оценки величин постулированных эффектов и для проверки того, соответствуют ли наблюдаемые данные требованиям предполагаемых причинных структур. [4]
Граница между тем, что является и чем не является структурной моделью уравнения, не всегда ясна, но модели SE часто содержат постулированные причинно-следственные связи между набором скрытых переменных (переменные, которые, как считается, существуют, но которые нельзя наблюдать напрямую, например, отношение, интеллект или психическое заболевание) и причинно-следственные связи, связывающие постулированные скрытые переменные с переменными, которые можно наблюдать и значения которых доступны в некотором наборе данных. Различия между стилями скрытых причинно-следственных связей, различия между наблюдаемыми переменными, измеряющими скрытые переменные, и различия в стратегиях статистической оценки приводят к набору инструментов SEM, включающему подтверждающий факторный анализ , подтверждающий композитный анализ , анализ пути , многогрупповое моделирование, продольное моделирование, моделирование пути с использованием частично наименьших квадратов , моделирование скрытого роста и иерархическое или многоуровневое моделирование. [5] [6] [7] [8] [9]
Исследователи SEM используют компьютерные программы для оценки силы и знака коэффициентов, соответствующих смоделированным структурным связям, например, чисел, связанных со стрелками на рисунке 1. Поскольку постулированная модель, такая как рисунок 1, может не соответствовать мирским силам, контролирующим наблюдаемые измерения данных, программы также предоставляют модельные тесты и диагностические подсказки, указывающие, какие индикаторы или какие компоненты модели могут вносить несоответствия между моделью и наблюдаемыми данными. Критика методов SEM намекает на: игнорирование доступных модельных тестов, проблемы в спецификации модели, тенденцию принимать модели без учета внешней валидности и потенциальные философские предубеждения. [10]
Большим преимуществом SEM является то, что все эти измерения и тесты происходят одновременно в одной статистической процедуре оценки, где все коэффициенты модели рассчитываются с использованием всей информации из наблюдаемых переменных. Это означает, что оценки более точны, чем если бы исследователь рассчитывал каждую часть модели отдельно. [11]
Моделирование структурных уравнений (SEM) начало отделяться от корреляции и регрессии, когда Сьюэлл Райт предоставил явные причинно-следственные интерпретации для набора уравнений в стиле регрессии, основанных на прочном понимании физических и физиологических механизмов, производящих прямые и косвенные эффекты среди его наблюдаемых переменных. [12] [13] [14] Уравнения оценивались как обычные уравнения регрессии, но существенный контекст для измеряемых переменных допускал четкое причинно-следственное, а не просто предсказательное понимание. О. Д. Дункан представил SEM в социальных науках в своей книге 1975 года [15] , и SEM расцвел в конце 1970-х и 1980-х годах, когда увеличение вычислительной мощности позволило проводить практическую оценку моделей. В 1987 году Гайдук [6] представил первое введение в структурное моделирование уравнений со скрытыми переменными, и вскоре за ним последовал популярный текст Боллена (1989). [16]
Различные, но математически связанные подходы к моделированию развивались в психологии, социологии и экономике. Ранняя работа Комиссии Коулза по оценке одновременных уравнений была сосредоточена на алгоритмах Купмана и Худа (1953) из транспортной экономики и оптимальной маршрутизации с оценкой максимального правдоподобия и закрытыми формами алгебраических вычислений, поскольку итеративные методы поиска решений были ограничены в дни до появления компьютеров. Схождение двух из этих направлений развития (факторный анализ из психологии и анализ пути из социологии через Дункана) создало нынешнее ядро SEM. Одна из нескольких программ, разработанных Карлом Йорескугом в Службе образовательного тестирования, LISREL [17] [18] [19], встраивала скрытые переменные (которые психологи знали как скрытые факторы из факторного анализа) в уравнения в стиле анализа пути (которые социологи унаследовали от Райта и Дункана). Факторно-структурированная часть модели включала ошибки измерения, которые допускали корректировку ошибок измерения, хотя и не обязательно безошибочную оценку, эффектов, связывающих различные постулированные скрытые переменные.
Следы исторической конвергенции традиций факторного анализа и анализа путей сохраняются в виде различия между измерениями и структурными частями моделей; и в виде продолжающихся разногласий по поводу тестирования моделей и того, должно ли измерение предшествовать или сопровождать структурные оценки. [20] [21] Рассмотрение факторного анализа как метода сокращения данных снижает важность тестирования, что контрастирует с оценкой анализа путей для тестирования постулированных причинных связей, когда результат теста может сигнализировать о неправильной спецификации модели. Трения между традициями факторного анализа и анализа путей продолжают всплывать в литературе.
Анализ путей Райта оказал влияние на Германа Вольда, ученика Вольда Карла Йорескуга и ученика Йорескуга Клааса Форнелла, но SEM так и не получил большого признания среди эконометристов США, возможно, из-за фундаментальных различий в целях моделирования и типичных структурах данных. Длительное разделение экономической ветви SEM привело к процедурным и терминологическим различиям, хотя глубокие математические и статистические связи сохранились. [22] [23] Экономическую версию SEM можно увидеть в обсуждениях эндогенности в SEMNET и в жаре, вызванном тем, что подход Джудеи Перл к причинности через направленные ациклические графы (DAG) сталкивается с экономическими подходами к моделированию. [4] Доступны обсуждения, сравнивающие и противопоставляющие различные подходы SEM [24] [25], но дисциплинарные различия в структурах данных и проблемы, мотивирующие экономические модели, делают воссоединение маловероятным. Перл [4] расширил SEM от линейных до непараметрических моделей и предложил причинные и контрфактуальные интерпретации уравнений. Непараметрические SEM позволяют оценивать общие, прямые и косвенные эффекты без каких-либо обязательств относительно линейности эффектов или предположений о распределениях членов ошибки. [25]
Анализы SEM популярны в социальных науках, поскольку компьютерные программы позволяют оценивать сложные причинно-следственные структуры, но сложность моделей вносит существенную изменчивость в качество результатов. Некоторые, но не все, результаты получены без «неудобств» понимания экспериментального дизайна, статистического контроля, последствий размера выборки и других особенностей, способствующих хорошему дизайну исследования. [ необходима цитата ]
Следующие соображения применимы к построению и оценке многих моделей структурных уравнений.
Для построения или спецификации модели необходимо уделить внимание:
Модели структурных уравнений пытаются отразить мирские силы, действующие для каузально однородных случаев, а именно случаев, запутанных в одних и тех же мирских каузальных структурах, но чьи значения причин различаются и которые, следовательно, обладают разными значениями переменных результата. Каузальная однородность может быть достигнута путем отбора случаев или путем разделения случаев в многогрупповой модели. Спецификация модели не является полной, пока исследователь не укажет:
Скрытый уровень модели состоит из эндогенных и экзогенных переменных . Эндогенные скрытые переменные — это переменные с истинной оценкой, постулируемые как получающие эффекты по крайней мере от одной другой смоделированной переменной. Каждая эндогенная переменная моделируется как зависимая переменная в уравнении регрессионного стиля. Экзогенные скрытые переменные — это фоновые переменные, постулируемые как вызывающие одну или несколько эндогенных переменных, и моделируются как предикторные переменные в уравнениях регрессионного стиля. Причинно-следственные связи между экзогенными переменными явно не моделируются, но обычно признаются путем моделирования экзогенных переменных как свободно коррелирующих друг с другом. Модель может включать промежуточные переменные — переменные, получающие эффекты от некоторых переменных, но также посылающие эффекты другим переменным. Как и в регрессии, каждой эндогенной переменной назначается остаточная или ошибочная переменная, инкапсулирующая эффекты недоступных и обычно неизвестных причин. Каждая скрытая переменная, экзогенная или эндогенная , рассматривается как содержащая истинные оценки случаев по этой переменной, и эти истинные оценки причинно вносят действительные/подлинные изменения в одну или несколько наблюдаемых/сообщаемых индикаторных переменных. [26]
Программа LISREL присваивала греческие имена элементам в наборе матриц для отслеживания различных компонентов модели. Эти имена стали относительно стандартной нотацией, хотя нотация была расширена и изменена для учета различных статистических соображений. [19] [6] [16] [27] Тексты и программы, «упрощающие» спецификацию модели с помощью диаграмм или с помощью уравнений, допускающих выбранные пользователем имена переменных, в фоновом режиме повторно преобразуют модель пользователя в некоторую стандартную форму матричной алгебры. «Упрощения» достигаются путем неявного введения «предположений» программы по умолчанию о характеристиках модели, с которыми пользователи якобы не должны беспокоиться. К сожалению, эти предположения по умолчанию легко скрывают компоненты модели, которые оставляют нераспознанные проблемы, таящиеся в структуре модели и базовых матрицах.
В SEM различают два основных компонента моделей: структурную модель , показывающую потенциальные причинно-следственные зависимости между эндогенными и экзогенными скрытыми переменными , и модель измерения, показывающую причинно-следственные связи между скрытыми переменными и индикаторами. Например, модели исследовательского и подтверждающего факторного анализа фокусируются на причинно-следственных связях измерений, в то время как модели путей более точно соответствуют скрытым структурным связям SEM.
Разработчики моделей указывают каждый коэффициент в модели как свободный для оценки или фиксированный на некотором значении. Свободные коэффициенты могут быть постулированными эффектами, которые исследователь хочет проверить, фоновыми корреляциями между экзогенными переменными или дисперсиями остаточных или ошибочных переменных, обеспечивающими дополнительные вариации эндогенных скрытых переменных. Фиксированные коэффициенты могут иметь значения, такие как значения 1,0 на рисунке 2, которые обеспечивают шкалы для скрытых переменных, или значения 0,0, которые утверждают причинно-следственные связи, такие как утверждение об отсутствии прямых эффектов (отсутствие стрелок), указывающих от академической успеваемости к любой из четырех шкал на рисунке 1. Программы SEM предоставляют оценки и тесты свободных коэффициентов, в то время как фиксированные коэффициенты вносят важный вклад в тестирование общей структуры модели. Также могут использоваться различные виды ограничений между коэффициентами. [27] [6] [16] Спецификация модели зависит от того, что известно из литературы, опыта исследователя с моделируемыми переменными-индикаторами и особенностей, изучаемых с использованием конкретной структуры модели.
Существует ограничение на то, сколько коэффициентов можно оценить в модели. Если точек данных меньше, чем количество оцененных коэффициентов, то полученная модель считается «неидентифицированной», и оценки коэффициентов получить невозможно. Взаимный эффект и другие причинно-следственные связи также могут помешать оценке. [28] [29] [27]
Коэффициенты модели, фиксированные на нуле, 1,0 или других значениях, не требуют оценки, поскольку они уже имеют заданные значения. Оценочные значения для свободных коэффициентов модели получаются путем максимизации соответствия или минимизации отличия от данных относительно того, какими были бы характеристики данных, если бы свободные коэффициенты модели приняли оцененные значения. Влияние модели на то, как должны выглядеть данные для определенного набора значений коэффициентов, зависит от: a) расположения коэффициентов в модели (например, какие переменные связаны/не связаны), b) характера связей между переменными (ковариации или эффекты; при этом эффекты часто предполагаются линейными), c) характера ошибок или остаточных переменных (часто предполагается, что они независимы или причинно-не связаны со многими переменными) и d) шкал измерения, соответствующих переменным (часто предполагается измерение на уровне интервала).
Более сильный эффект, связывающий две скрытые переменные, подразумевает, что индикаторы этих скрытых переменных должны быть более сильно коррелированы. Следовательно, разумной оценкой эффекта скрытой переменной будет любое значение, которое наилучшим образом соответствует корреляциям между индикаторами соответствующих скрытых переменных, а именно оценочное значение, максимизирующее совпадение с данными или минимизирующее различия с данными. При оценке максимального правдоподобия числовые значения всех свободных коэффициентов модели индивидуально корректируются (постепенно увеличиваются или уменьшаются от начальных начальных значений) до тех пор, пока они не максимизируют вероятность наблюдения выборочных данных, будь то данные ковариаций/корреляций переменных или фактических значений случаев на индикаторных переменных. Обычные оценки наименьших квадратов представляют собой значения коэффициентов, которые минимизируют квадратичные различия между данными и тем, как бы выглядели данные, если бы модель была правильно указана, а именно, если бы все оцененные характеристики модели соответствовали реальным характеристикам.
Соответствующая статистическая функция для максимизации или минимизации для получения оценок зависит от уровней измерения переменных (оценка, как правило, проще с измерениями на уровне интервалов, чем с номинальными или порядковыми мерами), и от того, где конкретная переменная появляется в модели (например, эндогенные дихотомические переменные создают больше трудностей при оценке, чем экзогенные дихотомические переменные). Большинство программ SEM предоставляют несколько вариантов того, что должно быть максимизировано или минимизировано для получения оценок коэффициентов модели. Выбор часто включает оценку максимального правдоподобия (MLE), полное информационное максимальное правдоподобие (FIML), обычные наименьшие квадраты (OLS), взвешенные наименьшие квадраты (WLS), диагонально взвешенные наименьшие квадраты (DWLS) и двухэтапный наименьшие квадраты. [27]
Одной из распространенных проблем является то, что оценочное значение коэффициента может быть недоопределено, поскольку оно недостаточно ограничено моделью и данными. Никакой уникальной наилучшей оценки не существует, если модель и данные вместе не ограничивают или не ограничивают значение коэффициента. Например, величина одной корреляции данных между двумя переменными недостаточна для предоставления оценок взаимной пары смоделированных эффектов между этими переменными. Корреляция может быть объяснена тем, что один из обратных эффектов сильнее другого эффекта, или другим эффектом сильнее первого, или эффектами равной величины. Недоопределенные оценки эффектов могут быть сделаны идентифицированными путем введения дополнительных ограничений модели и/или данных. Например, обратные эффекты могут быть сделаны идентифицированными путем ограничения одной оценки эффекта двойной, тройной или эквивалентной другой оценке эффекта [29] , но полученные оценки будут заслуживать доверия только в том случае, если дополнительное ограничение модели соответствует структуре мира. Данные о третьей переменной, которая напрямую вызывает только одну из пары взаимно причинно связанных переменных, также могут помочь в идентификации. [28] Ограничение третьей переменной, чтобы она не вызывала напрямую одну из взаимно-причинных переменных, нарушает симметрию, в противном случае мешая оценкам взаимного эффекта, поскольку эта третья переменная должна быть сильнее коррелирована с переменной, которую она вызывает напрямую, чем с переменной на «другом» конце взаимного эффекта, на которую она влияет только косвенно. [28] Обратите внимание, что это снова предполагает правильность каузальной спецификации модели, а именно, что действительно существует прямой эффект, ведущий от третьей переменной к переменной на этом конце взаимно-связанных эффектов, и нет прямого эффекта на переменную на «другом конце» взаимно связанной пары переменных. Теоретические требования к нулевым/нулевым эффектам предоставляют полезные ограничения, помогающие оценке, хотя теории часто не могут четко сообщить, какие эффекты якобы не существуют.
Оценка модели зависит от теории, данных, модели и стратегии оценки. Поэтому оценки модели учитывают:
Исследования, претендующие на проверку или «расследование» теории, требуют внимания к неслучайной несогласованности модели и данных. Оценка корректирует свободные коэффициенты модели для обеспечения наилучшего возможного соответствия данным. Выходные данные программ SEM включают матрицу, сообщающую о связях между наблюдаемыми переменными, которые наблюдались бы, если бы оцененные эффекты модели фактически контролировали значения наблюдаемых переменных. «Подгонка» модели сообщает о соответствии или несоответствии между подразумеваемыми моделью связями (часто ковариациями) и соответствующими наблюдаемыми связями между переменными. Большие и значимые различия между данными и следствиями модели указывают на проблемы. Вероятность, сопровождающая тест χ 2 ( хи-квадрат ), — это вероятность того, что данные могли возникнуть в результате случайных вариаций выборки, если оцененная модель представляла собой реальные основные силы популяции. Малая вероятность χ 2 сообщает, что было бы маловероятно, чтобы текущие данные возникли, если бы смоделированная структура представляла собой реальные причинные силы популяции, — с оставшимися различиями, приписываемыми случайным вариациям выборки.
Если модель остается несогласованной с данными, несмотря на выбор оптимальных оценок коэффициентов, честный исследовательский ответ сообщает и обращает внимание на эти доказательства (часто значимый тест модели χ 2 ). [30] Несоответствие модели данным за пределами случайности бросает вызов как оценкам коэффициентов, так и способности модели выносить суждение о структуре модели, независимо от того, возникает ли несоответствие из-за проблемных данных, ненадлежащей статистической оценки или неправильной спецификации модели. Оценки коэффициентов в моделях, несогласованных с данными («неудачных»), интерпретируются как отчеты о том, как мир будет выглядеть для того, кто верит в модель, которая противоречит имеющимся данным. Оценки в моделях, несогласованных с данными, не обязательно становятся «очевидно неправильными», становясь статистически странными или неправильно подписанными в соответствии с теорией. Оценки могут даже близко соответствовать требованиям теории, но остающаяся несогласованность данных делает соответствие оценок и теории неспособным оказать помощь. Неудачные модели остаются интерпретируемыми, но только как интерпретации, которые противоречат имеющимся доказательствам.
Репликация вряд ли обнаружит неправильно специфицированные модели, которые ненадлежащим образом соответствуют данным. Если данные репликации находятся в пределах случайных вариаций исходных данных, те же самые неправильные размещения коэффициентов, которые обеспечили ненадлежащее соответствие исходным данным, вероятно, также ненадлежащим образом подойдут к данным репликации. Репликация помогает обнаруживать такие проблемы, как ошибки в данных (допущенные разными исследовательскими группами), но особенно слаба при обнаружении ненадлежащих спецификаций после модификации исследовательской модели — например, когда конфирматорный факторный анализ (CFA) применяется к случайной второй половине данных после исследовательского факторного анализа (EFA) данных первой половины.
Индекс модификации — это оценка того, насколько «улучшится» соответствие модели данным (но не обязательно насколько улучшится структура модели), если конкретный текущий фиксированный коэффициент модели будет освобожден для оценки. Исследователи, сталкивающиеся с моделями, не соответствующими данным, могут легко освободить коэффициенты, которые индексы модификации сообщают как вероятно дающие существенные улучшения в соответствии. Это одновременно вносит существенный риск перехода от причинно-неправильной и несостоятельной модели к причинно-неправильной, но подходящей модели, поскольку улучшенное соответствие данным не дает гарантии того, что освобожденные коэффициенты являются по существу разумными или соответствуют миру. Исходная модель может содержать причинно-следственные неточности, такие как неправильно направленные эффекты или неверные предположения о недоступных переменных, и такие проблемы нельзя исправить путем добавления коэффициентов к текущей модели. Следовательно, такие модели остаются неправильно определенными, несмотря на более близкое соответствие, обеспечиваемое дополнительными коэффициентами. Подходящие, но несовместимые с реальностью модели особенно вероятны, если исследователь, приверженный определенной модели (например, факторной модели с желаемым числом факторов), добивается подгонки изначально неудачной модели путем вставки ковариаций ошибок измерения, «предложенных» индексами модификации. Маккаллум (1986) продемонстрировал, что «даже при благоприятных условиях модели, возникающие из поисковиков спецификаций, следует рассматривать с осторожностью». [31] Неправильная спецификация модели иногда может быть исправлена путем вставки коэффициентов, предложенных индексами модификации, но гораздо больше возможностей для исправления возникает при использовании нескольких индикаторов похожих, но существенно отличающихся скрытых переменных. [32]
«Принятие» несостоятельных моделей как «достаточно близких» также не является разумной альтернативой. Предостерегающий пример был предоставлен Брауном, МакКаллумом, Кимом, Андерсоном и Глейзером, которые обратились к математике, лежащей в основе того, почему тест χ 2 может иметь (хотя и не всегда имеет) значительную мощность для обнаружения неправильной спецификации модели. [33] Вероятность, сопровождающая тест χ 2 , — это вероятность того, что данные могли возникнуть в результате случайных вариаций выборки, если текущая модель с ее оптимальными оценками представляла собой реальные основные силы популяции. Малая вероятность χ 2 сообщает, что было бы маловероятно, чтобы текущие данные возникли, если бы текущая структура модели представляла собой реальные причинные силы популяции — с оставшимися различиями, приписываемыми случайным вариациям выборки. Браун, МакКаллум, Ким, Андерсен и Глейзер представили факторную модель, которую они считали приемлемой, несмотря на то, что модель существенно не соответствовала их данным согласно χ 2 . Ошибочность их утверждения о том, что близкое соответствие следует считать достаточно хорошим, была продемонстрирована Хайдуком, Пазкеркой-Робинсоном, Каммингсом, Леверсом и Бересом [34] , которые продемонстрировали подходящую модель для собственных данных Брауна и др., включив экспериментальную особенность, которую Браун и др. упустили из виду. Ошибка была не в математике индексов или в чрезмерной чувствительности тестирования χ2 . Ошибка была в том, что Браун, МакКаллум и другие авторы забыли, пренебрегли или упустили из виду, что нельзя доверять тому , чтобы степень плохого соответствия соответствовала характеру, местоположению или серьезности проблем в спецификации модели. [35]
Многие исследователи пытались оправдать переход на индексы соответствия вместо тестирования своих моделей, утверждая, что χ 2 увеличивается (и, следовательно, вероятность χ 2 уменьшается) с увеличением размера выборки (N). Существует две ошибки в дисконтировании χ 2 на этой основе. Во-первых, для правильных моделей χ 2 не увеличивается с увеличением N [30] , поэтому если χ 2 увеличивается с N, это само по себе является признаком того, что что-то явно проблемно. И, во-вторых, для моделей, которые явно неверно определены, увеличение χ 2 с N дает хорошие новости об увеличении статистической мощности для обнаружения неверной спецификации модели (а именно мощности для обнаружения ошибки II типа). Некоторые виды важных неверных спецификаций не могут быть обнаружены с помощью χ 2 [35], поэтому любое количество несоответствия, выходящее за рамки того, что может быть разумно получено случайными вариациями, требует отчета и рассмотрения. [36] [30] Тест модели χ 2 , возможно скорректированный [37] , является самым сильным доступным тестом модели структурного уравнения.
Многочисленные индексы соответствия количественно определяют, насколько близко модель соответствует данным, но все индексы соответствия страдают от логической трудности, заключающейся в том, что размер или количество плохого соответствия не согласованы достоверно с серьезностью или природой проблем, вызывающих несогласованность данных. [35] Модели с различными причинно-следственными структурами, которые одинаково хорошо соответствуют данным, называются эквивалентными моделями. [27] Такие модели являются эквивалентными по соответствию данным, хотя и не эквивалентны причинно, поэтому по крайней мере одна из так называемых эквивалентных моделей должна быть несовместима со структурой мира. Если между X и Y существует идеальная корреляция 1,0, и мы моделируем это как X вызывает Y, будет идеальное соответствие и нулевая остаточная ошибка. Но модель может не соответствовать миру, потому что Y может фактически вызывать X, или и X, и Y могут реагировать на общую причину Z, или мир может содержать смесь этих эффектов (например, как общая причина плюс эффект Y на X) или другие причинные структуры. Идеальное соответствие не говорит нам, что структура модели соответствует структуре мира, и это, в свою очередь, подразумевает, что приближение к идеальному соответствию не обязательно соответствует приближению к структуре мира — может быть, соответствует, может быть, нет. Это делает неверным для исследователя утверждение, что даже идеальное соответствие модели подразумевает, что модель правильно каузально специфицирована. Даже для умеренно сложных моделей точно эквивалентно-подходящие модели редки. Модели, почти соответствующие данным, согласно любому индексу, неизбежно вносят дополнительные потенциально важные, но неизвестные неверные спецификации модели. Эти модели представляют собой большее препятствие для исследования.
Эта логическая слабость делает все индексы соответствия «бесполезными», когда модель структурного уравнения существенно не согласуется с данными, [36] но несколько сил продолжают распространять использование индексов соответствия. Например, Даг Сорбом сообщил, что когда кто-то спросил Карла Йорескога, разработчика первой программы моделирования структурных уравнений, «Зачем вы тогда добавили GFI?» в вашу программу LISREL, Йореског ответил: «Ну, пользователи угрожают нам, говоря, что прекратят использовать LISREL, если он всегда выдает такие большие хи-квадраты. Поэтому нам пришлось придумать что-то, чтобы сделать людей счастливыми. GFI служит этой цели». [38] Доказательство χ2 несогласованности модели и данных было слишком статистически надежным, чтобы его можно было вытеснить или отбросить, но людям, по крайней мере, можно было предоставить способ отвлечься от «тревожных» доказательств. Карьерная прибыль все еще может быть накоплена путем разработки дополнительных индексов, отчетов об исследованиях поведения индексов и публикации моделей, намеренно скрывающих доказательства несоответствия модели данным под MDI (кучей отвлекающих индексов). Кажется, нет общего обоснования того, почему исследователь должен «принять» причинно-следственно неверную модель, а не пытаться исправить обнаруженные неточности спецификации. И некоторые части литературы, похоже, не заметили, что «принятие модели» (на основе «удовлетворения» значения индекса) страдает от усиленной версии критики, применяемой к «принятию» нулевой гипотезы. Вводные статистические тексты обычно рекомендуют заменять термин «принять» на «не удалось отвергнуть нулевую гипотезу», чтобы признать возможность ошибки II типа. Ошибка III типа возникает из-за «принятия» гипотезы модели, когда текущих данных достаточно, чтобы отвергнуть модель.
Является ли стремление исследователей искать структуру мира фундаментальным вопросом. Вытеснение тестовых доказательств несоответствия модели и данных путем сокрытия их за индексными утверждениями о приемлемом соответствии, вносит общедисциплинарные издержки отвлечения внимания от того, что дисциплина могла бы сделать для достижения структурно улучшенного понимания сути дисциплины. Дисциплина в конечном итоге платит реальные издержки за индексное вытеснение доказательств неправильной спецификации модели. Трения, созданные разногласиями по поводу необходимости исправления неправильной спецификации модели, вероятно, возрастут с ростом использования нефакторно-структурированных моделей и с использованием меньшего количества более точных индикаторов схожих, но, что важно, различных скрытых переменных. [32]
Соображения, имеющие отношение к использованию индексов соответствия, включают проверку:
Некоторые из наиболее часто используемых статистических показателей соответствия включают:
В следующей таблице приведены ссылки, документирующие эти и другие характеристики для некоторых распространенных индексов: RMSEA (среднеквадратичная ошибка аппроксимации), SRMR (стандартизированный среднеквадратический остаток), CFI (индекс подтверждающего соответствия) и TLI (индекс Такера-Льюиса). Дополнительные индексы, такие как AIC (информационный критерий Акаике), можно найти в большинстве введений в SEM. [27] Для каждой меры соответствия решение о том, что представляет собой достаточно хорошее соответствие между моделью и данными, отражает цель моделирования исследователя (возможно, оспаривание чьей-либо модели или улучшение измерения); следует ли заявлять, что модель была «протестирована»; и может ли исследователь «игнорировать» доказательства задокументированной индексом степени плохого соответствия. [30]
Исследователи согласны, что выборки должны быть достаточно большими, чтобы обеспечить стабильные оценки коэффициентов и разумную мощность тестирования, но нет общего консенсуса относительно конкретных требуемых размеров выборки или даже того, как определить соответствующие размеры выборки. Рекомендации основывались на количестве коэффициентов, которые должны быть оценены, количестве моделируемых переменных и моделировании Монте-Карло, рассматривающем конкретные коэффициенты модели. [27] Рекомендации по размеру выборки, основанные на отношении количества индикаторов к латентным значениям, ориентированы на факторы и не применяются к моделям, использующим отдельные индикаторы с фиксированными ненулевыми дисперсиями ошибок измерения. [32] В целом, для моделей среднего размера без статистически трудно оцениваемых коэффициентов требуемые размеры выборки (N) кажутся примерно сопоставимыми с N, необходимыми для регрессии, использующей все индикаторы.
Чем больше размер выборки, тем больше вероятность включения случаев, которые не являются причинно-следственно однородными. Следовательно, увеличение N для повышения вероятности возможности сообщить желаемый коэффициент как статистически значимый, одновременно увеличивает риск неправильной спецификации модели и мощность обнаружения неправильной спецификации. Исследователи, стремящиеся извлечь уроки из своего моделирования (включая потенциальное изучение того, что их модель требует корректировки или замены), будут стремиться к максимально большому размеру выборки, насколько это допускается финансированием и их оценкой вероятной причинной неоднородности/однородности на основе популяции. Если доступное N огромно, подмножества случаев моделирования могут контролировать переменные, которые в противном случае могли бы нарушить причинную однородность. Исследователи, опасающиеся, что им, возможно, придется сообщать о недостатках своей модели, разрываются между желанием большего N, чтобы обеспечить достаточную мощность для обнаружения интересующих структурных коэффициентов, и избеганием мощности, способной сигнализировать о несоответствии модели данным. Огромное разнообразие структур моделей и характеристик данных позволяет предположить, что адекватные размеры выборки можно было бы с пользой определить, приняв во внимание опыт других исследователей (как положительный, так и отрицательный) с моделями сопоставимого размера и сложности, которые оценивались с использованием аналогичных данных.
Причинно-следственные интерпретации моделей SE являются наиболее ясными и понятными, но эти интерпретации будут ошибочными/неправильными, если структура модели не соответствует причинно-следственной структуре мира. Следовательно, интерпретация должна касаться общего статуса и структуры модели, а не только оценочных коэффициентов модели. Соответствует ли модель данным и/или как модель пришла к соответствию данным, имеют первостепенное значение для интерпретации. Соответствие данных, полученное путем исследования или следования последовательным индексам модификации, не гарантирует, что модель неверна, но вызывает серьезные сомнения, поскольку эти подходы склонны к неправильному моделированию характеристик данных. Например, исследование с целью выяснить, сколько факторов требуется, предвосхищает обнаружение того, что данные не структурированы факторами, особенно если факторную модель «убедили» соответствовать путем включения ковариаций ошибок измерения. Способность данных говорить против постулируемой модели постепенно подрывается с каждым необоснованным включением эффекта «предложенного индекса модификации» или ковариации ошибок. Становится чрезвычайно сложно восстановить правильную модель, если исходная/базовая модель содержит несколько неверных спецификаций. [46]
Оценки прямого эффекта интерпретируются параллельно с интерпретацией коэффициентов в уравнениях регрессии, но с причинно-следственной привязкой. Каждое единичное увеличение значения причинной переменной рассматривается как производящее изменение расчетной величины значения зависимой переменной с учетом контроля или корректировки для всех других оперативных/моделируемых причинных механизмов. Косвенные эффекты интерпретируются аналогично, причем величина конкретного косвенного эффекта равна произведению ряда прямых эффектов, составляющих этот косвенный эффект. Вовлеченными единицами являются реальные шкалы значений наблюдаемых переменных и назначенные значения шкалы для скрытых переменных. Указанный/фиксированный 1,0 эффект скрытой переменной на конкретный индикатор координирует шкалу этого индикатора со шкалой скрытой переменной. Предположение о том, что остальная часть модели остается постоянной или неизменной, может потребовать дисконтирования косвенных эффектов, которые в реальном мире могут быть одновременно вызваны реальным единичным увеличением. И само по себе увеличение единицы может быть несовместимым с тем, что возможно в реальном мире, поскольку может не быть известного способа изменить значение причинной переменной. Если модель корректирует ошибки измерения, корректировка позволяет интерпретировать эффекты скрытого уровня как относящиеся к вариациям в истинных оценках. [26]
Интерпретации SEM наиболее радикально отличаются от интерпретаций регрессии, когда сеть причинных коэффициентов связывает скрытые переменные, поскольку регрессии не содержат оценок косвенных эффектов. Интерпретации SEM должны передавать последствия моделей косвенных эффектов, которые переносят эффекты от фоновых переменных через промежуточные переменные к нижестоящим зависимым переменным. Интерпретации SEM способствуют пониманию того, как множественные мирские причинные пути могут работать в координации или независимо, или даже противодействовать друг другу. Прямые эффекты могут быть противодействованы (или усилены) косвенными эффектами, или их корреляционные последствия могут быть противодействованы (или усилены) эффектами общих причин. [15] Значение и интерпретация конкретных оценок должны быть контекстуализированы в полной модели.
Интерпретация модели SE должна связывать конкретные причинные сегменты модели с их дисперсией и ковариационными последствиями. Один прямой эффект сообщает, что дисперсия в независимой переменной производит определенное количество вариации в значениях зависимой переменной, но причинные детали того, что именно заставляет это происходить, остаются неопределенными, поскольку один коэффициент эффекта не содержит подкомпонентов, доступных для интеграции в структурированную историю о том, как возникает этот эффект. Более мелкозернистая модель SE, включающая переменные, промежуточные между причиной и следствием, потребовалась бы для предоставления характеристик, составляющих историю о том, как функционирует любой один эффект. Пока такая модель не появится, каждый оцененный прямой эффект сохраняет оттенок неизвестности, тем самым вызывая суть теории. Параллельная существенная неизвестность будет сопровождать каждый оцененный коэффициент даже в более мелкозернистой модели, поэтому чувство фундаментальной тайны никогда полностью не искореняется из моделей SE.
Даже если каждый смоделированный эффект неизвестен за пределами идентичности задействованных переменных и предполагаемой величины эффекта, структуры, связывающие несколько смоделированных эффектов, предоставляют возможности для выражения того, как функционируют вещи, чтобы координировать наблюдаемые переменные, тем самым предоставляя полезные возможности интерпретации. Например, общая причина вносит вклад в ковариацию или корреляцию между двумя затронутыми переменными, потому что если значение причины увеличивается, значения обоих эффектов также должны увеличиваться (предполагая положительные эффекты), даже если мы не знаем полной истории, лежащей в основе каждой причины. [15] (Корреляция — это ковариация между двумя переменными, которые обе были стандартизированы, чтобы иметь дисперсию 1,0). Другой интерпретационный вклад может быть сделан путем выражения того, как две причинные переменные могут обе объяснять дисперсию в зависимой переменной, а также того, как ковариация между двумя такими причинами может увеличивать или уменьшать объясненную дисперсию в зависимой переменной. То есть интерпретация может включать объяснение того, как модель эффектов и ковариаций может способствовать уменьшению дисперсии зависимой переменной. [47] Понимание причинных импликаций неявно связано с пониманием «контроля» и потенциального объяснения того, почему некоторые переменные, а не другие, должны контролироваться. [4] [48] По мере того, как модели становятся более сложными, эти фундаментальные компоненты могут объединяться неинтуитивными способами, например, объясняя, как может не быть корреляции (нулевая ковариация) между двумя переменными, несмотря на то, что переменные связаны прямым ненулевым причинным эффектом. [15] [16] [6] [29]
Статистическая незначимость оценки эффекта указывает на то, что оценка может довольно легко возникнуть как случайная вариация выборки вокруг нулевого/нулевого эффекта, поэтому интерпретация оценки как реального эффекта становится двусмысленной. Как и в регрессии, доля дисперсии каждой зависимой переменной, объясняемая вариациями в смоделированных причинах, предоставляется R 2 , хотя следует использовать Blocked-Error R 2 , если зависимая переменная вовлечена в обратные или циклические эффекты, или если она имеет переменную ошибки, коррелированную с переменной ошибки любого предиктора. [49]
Предостережение, содержащееся в разделе «Оценка модели», заслуживает повторения. Интерпретация должна быть возможна независимо от того, согласуется ли модель с данными или нет. Оценки сообщают, как мир будет выглядеть для того, кто верит в модель, — даже если эта вера необоснованна, поскольку модель оказывается неверной. Интерпретация должна признавать, что коэффициенты модели могут соответствовать или не соответствовать «параметрам», поскольку коэффициенты модели могут не иметь соответствующих структурных особенностей мира.
Добавление новых скрытых переменных, входящих или выходящих из исходной модели в нескольких четких причинных местах/переменных, способствует обнаружению неверных спецификаций модели, которые в противном случае могли бы разрушить интерпретации коэффициентов. Корреляции между новыми скрытыми показателями и всеми исходными показателями способствуют тестированию структуры исходной модели, поскольку несколько новых и сфокусированных коэффициентов эффектов должны работать в координации с исходными прямыми и косвенными эффектами модели, чтобы согласовывать новые показатели с исходными показателями. Если структура исходной модели была проблемной, разреженных новых причинных связей будет недостаточно для координации новых показателей с исходными показателями, тем самым сигнализируя о несоответствии коэффициентов исходной модели через несогласованность модели и данных. [29] Корреляционные ограничения, основанные на нулевых/нулевых коэффициентах эффектов, и коэффициенты, которым присвоены фиксированные ненулевые значения, способствуют как тестированию модели, так и оценке коэффициентов и, следовательно, заслуживают признания в качестве каркаса, поддерживающего оценки и их интерпретацию. [29]
Интерпретации становятся все более сложными для моделей, содержащих взаимодействия, нелинейности, множественные группы, множественные уровни и категориальные переменные. [27] Эффекты, касающиеся причинно-следственных связей, взаимных эффектов или коррелированных остатков, также требуют слегка пересмотренных интерпретаций. [6] [29]
Тщательная интерпретация как провальных, так и подходящих моделей может обеспечить исследовательский прогресс. Чтобы быть надежной, модель должна исследовать академически информативные причинные структуры, подгонять применимые данные под понятные оценки и не включать пустые коэффициенты. [50] Надежные подходящие модели встречаются реже, чем провальные модели или модели, ненадлежащим образом забитые для подгонки, но подходящие подходящие модели возможны. [34] [51] [52] [53]
Множественные способы концептуализации моделей PLS [54] усложняют интерпретацию моделей PLS. Многие из приведенных выше комментариев применимы, если разработчик моделей PLS придерживается реалистичной точки зрения, стремясь обеспечить, чтобы их смоделированные индикаторы сочетались таким образом, чтобы соответствовать некоторой существующей, но недоступной скрытой переменной. Некаузальные модели PLS, такие как те, которые фокусируются в первую очередь на R 2 или предсказательной силе вне выборки, изменяют критерии интерпретации, уменьшая беспокойство о том, имеют ли коэффициенты модели мирские аналоги. Фундаментальные особенности, отличающие пять перспектив моделирования PLS, обсуждаемых Ригдоном, Сарстедтом и Рингле [54], указывают на различия в целях разработчиков моделей PLS и соответствующие различия в характеристиках модели, требующих интерпретации.
Следует проявлять осторожность при заявлениях о причинности, даже если были проведены эксперименты или упорядоченные по времени исследования. Термин причинная модель следует понимать как «модель, которая передает причинные предположения», а не обязательно модель, которая производит подтвержденные причинные выводы — может быть, да, может быть, нет. Сбор данных в нескольких временных точках и использование экспериментального или квазиэкспериментального дизайна может помочь исключить определенные конкурирующие гипотезы, но даже рандомизированные эксперименты не могут полностью исключить угрозы причинным утверждениям. Ни один исследовательский дизайн не может полностью гарантировать причинные структуры. [4]
Моделирование структурных уравнений полно противоречий. Исследователи из традиции факторного анализа обычно пытаются сократить наборы множественных индикаторов до меньшего количества, более управляемых, шкал или факторных оценок для последующего использования в моделях с путевой структурой. Это представляет собой пошаговый процесс, в котором начальный этап измерения предоставляет шкалы или факторные оценки, которые должны использоваться позже в модели с путевой структурой. Этот пошаговый подход кажется очевидным, но на самом деле сталкивается с серьезными базовыми недостатками. Сегментация на этапы мешает тщательной проверке того, действительно ли шкалы или факторные оценки представляют индикаторы и/или достоверно сообщают о скрытых эффектах уровня. Модель структурных уравнений, одновременно включающая как структуры измерения, так и скрытого уровня, не только проверяет, надлежащим ли образом скрытые факторы координируют индикаторы, но и проверяет, одновременно ли тот же скрытый фактор надлежащим образом координирует индикаторы каждого скрытого фактора с индикаторами предполагаемых причин и/или последствий этого скрытого фактора. [29] Если латент не способен выполнять оба этих стиля координации, то ставится под сомнение обоснованность этого латентного фактора, а также шкала или факторные баллы, претендующие на измерение этого латентного фактора. Разногласия вращались вокруг уважения или неуважения к доказательствам, оспаривающим обоснованность постулируемых латентных факторов. Кипящие, иногда кипящие, дискуссии привели к специальному выпуску журнала Structural Equation Modeling, посвященному целевой статье Хайдука и Глейзера [20], за которой последовало несколько комментариев и возражение, [21] все это стало доступно бесплатно благодаря усилиям Джорджа Маркулидеса.
Эти дискуссии подогревали разногласия по поводу того, следует ли тестировать модели структурных уравнений на предмет согласованности с данными, и тестирование моделей стало следующим фокусом дискуссий. Ученые, имеющие историю моделирования путей, как правило, защищали тщательное тестирование моделей, в то время как те, у кого была история факторов, как правило, защищали индексацию соответствия, а не тестирование соответствия. Эти дискуссии привели к целевой статье в Personality and Individual Differences Пола Барретта [36], который сказал: «На самом деле, я бы теперь рекомендовал запретить ВСЕ подобные индексы от появления в любой статье как показатель «приемлемости» модели или «степени несоответствия»». [36] (стр. 821). Статья Барретта также сопровождалась комментариями с обеих точек зрения. [50] [55]
Споры по поводу тестирования моделей пошли на убыль, поскольку четкое сообщение о существенном несоответствии модели и данных стало обязательным. Ученые не могут игнорировать или не сообщать о доказательствах только потому, что им не нравится то, что сообщают доказательства. [30] Требование внимания к доказательствам, указывающим на неправильную спецификацию модели, лежит в основе более недавней озабоченности по поводу «эндогенности» — стиля неправильной спецификации модели, который мешает оценке из-за отсутствия независимости переменных ошибок/остатков. В целом, споры о причинной природе моделей структурных уравнений, включая факторные модели, также пошли на убыль. Стэн Мулайк, ярый сторонник факторного анализа, признал причинную основу факторных моделей. [56] Комментарии Боллена и Перла относительно мифов о причинности в контексте SEM [25] усилили центральную роль причинного мышления в контексте SEM.
Более краткий спор, сосредоточенный на конкурирующих моделях. Сравнение конкурирующих моделей может быть очень полезным, но есть фундаментальные проблемы, которые нельзя решить, создав две модели и сохранив более подходящую модель. Статистическая сложность презентаций, таких как Levy and Hancock (2007), [57] , например, позволяет легко упустить из виду, что исследователь может начать с одной ужасной модели и одной ужасной модели, а закончить, сохранив структурно ужасную модель, потому что какой-то индекс сообщает, что она лучше подходит, чем ужасная модель. К сожалению, даже в остальном сильные тексты SEM, такие как Kline (2016) [27], остаются тревожно слабыми в своем представлении тестирования моделей. [58] В целом, вклад, который может быть сделан моделированием структурных уравнений, зависит от тщательной и подробной оценки модели, даже если неудачная модель оказывается лучшей из доступных.
Еще один спор, который затронул периферию предыдущих споров, ждет своего часа. [ требуется ссылка ] Факторные модели и теоретико-встроенные факторные структуры, имеющие несколько индикаторов, как правило, терпят неудачу, а исключение слабых индикаторов, как правило, снижает несоответствие модели данным. Уменьшение количества индикаторов приводит к беспокойству и спорам по поводу минимального количества индикаторов, необходимых для поддержки скрытой переменной в модели структурного уравнения. Исследователей, привязанных к факторной традиции, можно убедить сократить количество индикаторов до трех на скрытую переменную, но три или даже два индикатора все еще могут не соответствовать предлагаемой общей причине базового фактора. Хайдук и Литтвей (2012) [32] обсудили, как думать об ошибке измерения, защищать ее и корректировать ее, когда для каждой моделируемой скрытой переменной используется только один индикатор. Отдельные индикаторы эффективно использовались в моделях SE в течение длительного времени, [51], но споры остаются только такими же далекими, как и рецензент, который рассматривал измерение только с точки зрения факторного анализа.
Хотя эти противоречия и уменьшаются, следы этих противоречий разбросаны по всей литературе по SEM, и вы можете легко спровоцировать разногласия, спросив: Что следует делать с моделями, которые существенно не согласуются с данными? Или спросив: Перевешивает ли простота модели уважение к доказательствам несогласованности данных? Или, какой вес следует придавать индексам, которые показывают близкое или не очень близкое соответствие данных некоторым моделям? Или, должны ли мы быть особенно снисходительными к экономным моделям, которые не согласуются с данными, и «вознаграждать» их? Или, учитывая, что RMSEA потворствует игнорированию некоторых реальных несоответствий для каждой степени свободы модели, не означает ли это, что люди, тестирующие модели с нулевыми гипотезами ненулевого RMSEA, проводят неполноценное тестирование моделей? Для убедительного ответа на такие вопросы требуются значительные различия в статистической сложности, хотя ответы, скорее всего, будут сосредоточены на нетехническом вопросе о том, обязаны ли исследователи сообщать и уважать доказательства.
Программы моделирования структурных уравнений значительно различаются по своим возможностям и требованиям пользователей. [66]
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ){{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )