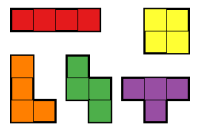
Тетромино — это геометрическая фигура, состоящая из четырёх квадратов , соединённых ортогонально (т. е. по краям, а не по углам). [1] [2] Тетромино, как и домино и пентамино , являются особым типом полимино . Соответствующий поликуб , называемый тетракубом , представляет собой геометрическую фигуру, состоящую из четырёх кубов, соединённых ортогонально.
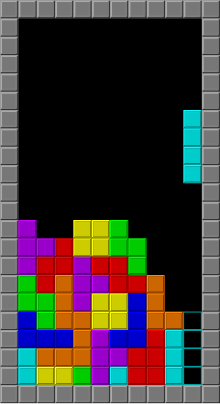
Популярное использование тетромино — в видеоигре «Тетрис», созданной советским гейм-дизайнером Алексеем Пажитновым , в которой они называются тетримино . [3] Тетромино, используемые в игре, — это именно односторонние тетромино.
Полимино образуются путем соединения единичных квадратов по их ребрам. Свободное полимино — это полимино, рассматриваемое с точностью до конгруэнтности . То есть два свободных полимино одинаковы, если существует комбинация переносов , вращений и отражений , которая превращает одно в другое. Свободное тетромино — это свободное полимино, составленное из четырех квадратов. Существует пять свободных тетромино.
Свободные тетромино имеют следующую симметрию:
Односторонние тетромино — это тетромино, которые можно переводить и вращать, но нельзя отражать. Они используются и в подавляющем большинстве ассоциируются с Тетрисом . Существует семь различных односторонних тетромино. Эти тетромино названы по буквам алфавита, на которые они больше всего похожи. Тетромино «I», «O» и «T» обладают отражательной симметрией, поэтому не имеет значения, считаются ли они свободными тетромино или односторонними тетромино. Остальные четыре тетромино, «J», «L», «S» и «Z», демонстрируют явление, называемое хиральностью . J и L являются отражениями друг друга, а S и Z являются отражениями друг друга.
Как свободные тетрамино, J эквивалентен L, а S эквивалентен Z, но в двух измерениях и без отражений невозможно преобразовать J в L или S в Z.
Фиксированные тетромино допускают только трансляцию, но не вращение или отражение. Существует два отдельных фиксированных I-тетромино, четыре J, четыре L, один O, два S, четыре T и два Z, что в общей сложности составляет 19 фиксированных тетромино.
Один набор свободных тетромино или односторонних тетромино не может поместиться в прямоугольник. Это можно показать с помощью доказательства, похожего на аргумент изуродованной шахматной доски . Прямоугольник 5×4 с шахматным узором имеет 20 квадратов, содержащих 10 светлых квадратов и 10 темных квадратов, но полный набор свободных тетромино имеет либо 11 темных квадратов и 9 светлых квадратов, либо 11 светлых квадратов и 9 темных квадратов. Это связано с тем, что тетромино T имеет либо 3 темных квадрата и один светлый квадрат, либо 3 светлых квадрата и один темный квадрат, в то время как все остальные тетромино имеют по 2 темных квадрата и 2 светлых квадрата. Аналогично, прямоугольник 7×4 имеет 28 квадратов, содержащих 14 квадратов каждого оттенка, но набор односторонних тетромино имеет либо 15 темных квадратов и 13 светлых квадратов, либо 15 светлых квадратов и 13 темных квадратов. По сути, любое нечетное количество наборов для любого типа не может поместиться в прямоугольник. Кроме того, 19 фиксированных тетромино не могут поместиться в прямоугольник 4×19. Это было обнаружено путем исчерпания всех возможностей в компьютерном поиске.
Дальнейшим следствием того, что тетрамино T имеет 3 квадрата одного цвета и 1 квадрат другого цвета, является то, что любой прямоугольник, содержащий четное число квадратов, должен содержать четное число тетрамино T. И наоборот, любые прямоугольники, содержащие нечетное число квадратов, должны содержать нечетное число тетрамино T.
Все три набора тетромино подходят для прямоугольников с отверстиями:
Два набора свободных или односторонних тетрамино можно вписать в прямоугольник разными способами, как показано ниже:
Название «тетромино» представляет собой комбинацию префикса тетра- «четыре» (от древнегреческого τετρα- ), и « домино ». Название было введено Соломоном В. Голомбом в 1953 году вместе с другой номенклатурой, связанной с полимино. [4] [1]
Каждый из пяти свободных тетромино имеет соответствующий тетракуб, который является тетромино, выдавленным одной единицей. J и L являются одним и тем же тетракубом, как и S и Z, потому что один из них может быть повернут вокруг оси, параллельной плоскости тетромино, чтобы сформировать другой. Возможны еще три тетракуба, все они создаются путем помещения единичного куба на изогнутый трикуб :
Тетракубы могут быть упакованы в двухслойные 3D-коробки несколькими способами, в зависимости от размеров коробки и критериев включения. Они показаны как на наглядных, так и на текстовых диаграммах. Для коробок, использующих два набора одинаковых деталей, на наглядной диаграмме каждый набор изображен как более светлый или более темный оттенок одного и того же цвета. На текстовой диаграмме каждый набор изображен как имеющий заглавную или строчную букву. На текстовой диаграмме верхний слой находится слева, а нижний слой — справа.
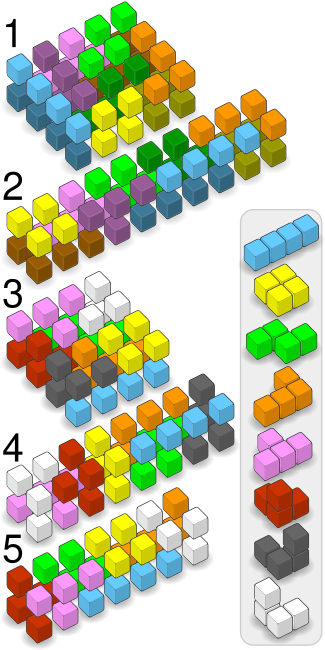
1.) Коробка 2×4×5, заполненная двумя наборами бесплатных тетромино:ZZT т I л TTT iLZZ т I лллтиL zzt I oozziLLOOI оо OO я2.) Коробка 2×2×10, заполненная двумя наборами бесплатных тетромино:LLL zz ZZTOO oozz ZZTTT lLIIII ттт OO ооооооо3.) Коробка 2×4×4, заполненная одним набором всех тетромино:FTTTFZZBФФТБЗЗББООЛДЛЛЛДООДДИИИИИ4.) Коробка 2×2×8, заполненная одним набором всех тетромино:ДЗЗЛОТТДЛЛЛОБФФDDZZOBTFIIIIOBBF5.) Коробка 2×2×7, заполненная тетромино, без зеркальных элементов:LLLZZBBLCOOZZBCIIIITBCCOOTTT