Охотничьи колебания

Автоколебания около равновесия, которые обычно нежелательны

Колебание качения на железнодорожных колесных парах

Охотничьи колебания — это автоколебания , обычно нежелательные, около равновесия . ^[1] Выражение вошло в употребление в 19 веке и описывает, как система «охотится» за равновесием. ^[1] Выражение используется для описания явлений в таких разнообразных областях, как электроника, авиация, биология и железнодорожное машиностроение. ^[1]

Железнодорожные колесные пары

Классическое колебательное движение — это колебательное движение железнодорожного транспортного средства (часто называемое колебанием тележки или колебанием тележки ), вызванное конусным действием, от которого зависит курсовая устойчивость сцепной железной дороги . Оно возникает из-за взаимодействия сил сцепления и сил инерции . На низкой скорости преобладает сцепление, но по мере увеличения скорости силы сцепления и силы инерции становятся сопоставимыми по величине, и колебание начинается на критической скорости. Выше этой скорости движение может быть интенсивным, повреждая рельсы и колеса и потенциально вызывая сход с рельсов . Проблема не возникает в системах с дифференциалом , поскольку действие зависит от вращения обоих колес колесной пары с одинаковой угловой скоростью, хотя дифференциалы, как правило, редки, и вместо этого колеса обычных поездов закреплены на осях парами. Некоторые поезда, такие как Talgo 350 , не имеют дифференциала, однако они в основном не подвержены колебанию, поскольку большинство их колес вращаются независимо друг от друга. Однако колеса силового вагона могут быть затронуты вилянием, поскольку колеса силового вагона закреплены на осях парами, как в обычных тележках. Менее конические колеса и тележки, оснащенные независимыми колесами, которые вращаются независимо друг от друга и не закреплены на оси парами, дешевле, чем подходящий дифференциал для тележек поезда. ^[2]

Проблема была впервые замечена в конце 19 века, когда скорости поездов стали достаточно высокими, чтобы столкнуться с ней. Серьёзные усилия по противодействию ей были предприняты в 1930-х годах, что привело к появлению удлинённых тележек и тележки с боковым демпфированием . При разработке японского Shinkansen использовались менее конические колёса и другие изменения конструкции, чтобы увеличить скорость конструкции тележки свыше 225 км/ч (140 миль/ч). Достижения в области проектирования колёс и тележек, основанные на научно-исследовательских и опытно-конструкторских работах в Европе и Японии, значительно увеличили скорость стальных колёсных систем по сравнению с теми, которые были достигнуты оригинальным Shinkansen , в то время как преимущество обратной совместимости позволяет такой технологии доминировать над альтернативами, такими как системы на воздушной подушке и магнитной подвеске . Рекорд скорости для поездов со стальными колёсами принадлежит французскому TGV — 574,9 км/ч (357 миль/ч).

Кинематический анализ

Кинематика конусного действия железнодорожного колеса

Хотя качественное описание дает некоторое понимание явления, более глубокое понимание неизбежно требует математического анализа динамики транспортного средства . Даже в этом случае результаты могут быть лишь приблизительными.

Кинематическое описание имеет дело с геометрией движения, без ссылки на силы, вызывающие его, поэтому анализ начинается с описания геометрии колесной пары, движущейся по прямой. Поскольку второй закон Ньютона связывает силы с ускорением тел, действующие силы затем могут быть выведены из кинематики путем вычисления ускорений компонентов. Однако если эти силы изменяют кинематическое описание (как в этом случае), то результаты могут быть лишь приблизительно правильными.

Предположения и нематематическое описание

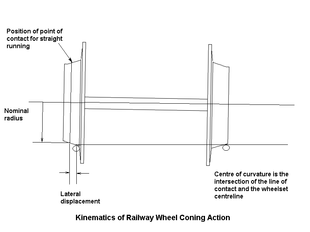
Это кинематическое описание делает ряд упрощающих предположений, поскольку оно пренебрегает силами. Во-первых, оно предполагает, что сопротивление качению равно нулю. Колесная пара (не прикрепленная к поезду или грузовику ) толкается вперед по прямой и ровной дороге. Колесная пара начинает движение по инерции и никогда не замедляется, поскольку нет никаких сил (за исключением направленных вниз сил на колесную пару, которые заставляют ее прилипать к пути и не скользить). Если изначально колесная пара отцентрирована на железнодорожном пути, то эффективные диаметры каждого колеса одинаковы, и колесная пара катится по пути по идеально прямой линии вечно. Но если колесная пара немного смещена от центра, так что эффективные диаметры (или радиусы) различны, то колесная пара начинает двигаться по кривой радиусом R (в зависимости от этих радиусов колесной пары и т. д.; будет выведено позже). Проблема заключается в том, чтобы с помощью кинематических рассуждений найти траекторию движения колесной пары, или, точнее, траекторию центра колесной пары, спроецированную вертикально на дорожное полотно в центре пути. Это траектория на плоскости ровной земной поверхности и нанесенная на графический график x - y , где x - расстояние вдоль железной дороги, а y - "ошибка слежения", отклонение центра колесной пары от прямой линии железной дороги, проходящей по центру пути (посередине между двумя рельсами).

Чтобы проиллюстрировать, что траектория движения колесной пары следует по кривой, можно положить гвоздь или шуруп на плоскую поверхность стола и подтолкнуть его. Он покатится по круговой кривой, потому что гвоздь или шуруп похож на колесную пару с колесами совершенно разного диаметра. Головка аналогична колесу большого диаметра, а заостренный конец похож на колесо малого диаметра. В то время как гвоздь или шуруп будет поворачиваться по полной окружности (и больше), железнодорожная колесная пара ведет себя по-другому, потому что как только она начинает поворачиваться по кривой, эффективные диаметры изменяются таким образом, что уменьшают кривизну пути. Обратите внимание, что «радиус» и «кривизна» относятся к кривизне траектории движения колесной пары, а не к кривизне железной дороги, поскольку это идеально прямой путь. По мере того, как колесная пара катится, кривизна уменьшается, пока колеса не достигнут точки, где их эффективные диаметры равны, и путь больше не будет кривым. Но траектория имеет наклон в этой точке (это прямая линия, которая пересекает по диагонали осевую линию пути), так что она перескакивает через осевую линию пути, и эффективные диаметры меняются на противоположные (ранее колесо меньшего диаметра становится большего диаметра и наоборот). Это приводит к тому, что колесная пара движется по кривой в противоположном направлении. Она снова перескакивает через осевую линию, и это явление продолжается бесконечно, причем колесная пара колеблется из стороны в сторону. Обратите внимание, что гребень колеса никогда не соприкасается с рельсом. В этой модели предполагается, что рельсы всегда соприкасаются с беговой дорожкой колеса вдоль одной и той же линии на головке рельса, что предполагает, что рельсы имеют ножевидную форму и соприкасаются с беговой дорожкой колеса только вдоль линии (нулевой ширины).

Математический анализ

Поезд остается на пути благодаря конической форме поверхностей катания колес . Если колесная пара смещена в одну сторону на величину y (ошибка слежения), радиус поверхности катания, соприкасающейся с рельсом с одной стороны, уменьшается, а с другой стороны увеличивается. Угловая скорость одинакова для обоих колес (они соединены жесткой осью ), поэтому поверхность катания большего диаметра ускоряется, а меньшего замедляется. Колесная пара поворачивается вокруг центра кривизны, определяемого пересечением образующей конуса, проходящего через точки соприкосновения с колесами на рельсах, и оси колесной пары. Применяя подобные треугольники , для радиуса поворота имеем:

Расчет радиуса поворота

${\displaystyle {\frac {1}{R}}={\frac {2ky}{rd}}}$

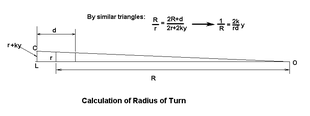
где d — ширина колеи , r — радиус колеса при движении по прямой, а k — конусность протектора (наклон протектора в горизонтальном направлении, перпендикулярном рельсу).

Путь колесной пары относительно прямого пути определяется функцией y ( x ), где x — это движение по пути. Иногда это называют ошибкой слежения. ^{[3] При условии,} что направление движения остается более или менее параллельным рельсам, кривизна пути может быть связана со второй производной y по расстоянию вдоль пути приблизительно как ^[4]

${\displaystyle \left|{\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}\right|\approx {\frac {1}{R}}}$

Отсюда следует, что траектория вдоль трассы описывается уравнением: ^[5]

${\displaystyle {\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}=-\left({\frac {2k}{rd}}\right)y}$

Это простое гармоническое движение, имеющее длину волны:

${\displaystyle \lambda =2\pi {\sqrt {\frac {rd}{2k}}}}$ известная как формула Клингеля (выведена в 1883 году) ^[6]

Этот кинематический анализ подразумевает, что поезда все время качаются из стороны в сторону. Фактически, это колебание затухает ниже критической скорости, и езда, соответственно, становится более комфортной. Кинематический результат игнорирует силы, вызывающие движение. Их можно проанализировать с использованием концепции проскальзывания (нелинейного), но их довольно сложно количественно оценить, поскольку они возникают из-за упругой деформации колеса и рельса в областях контакта. Они являются предметом механики фрикционного контакта ; ранняя презентация, которая включает эти эффекты в анализ движения охоты, была представлена ​​Картером. ^[7] См. Knothe ^[8] для исторического обзора.

Если движение практически параллельно рельсам, то угловое смещение колесной пары определяется по формуле: ${\displaystyle \left(\theta \right)}$

${\displaystyle \theta ={\frac {\operatorname {d} y}{\operatorname {d} x}}}$

Следовательно:

${\displaystyle {\begin{aligned}{\frac {\operatorname {d} \theta }{\operatorname {d} x}}&={\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}=-\left({\frac {2k}{rd}}\right)y\\{\frac {\operatorname {d} ^{2}\theta }{\operatorname {d} x^{2}}}&=-\left({\frac {2k}{rd}}\right){\frac {\operatorname {d} y}{\operatorname {d} x}}=-\left({\frac {2k}{rd}}\right)\theta \end{aligned}}}$

Угловое отклонение также следует простому гармоническому движению, которое отстает от бокового движения на четверть цикла. Во многих системах, которые характеризуются гармоническим движением, включающим два различных состояния (в данном случае отклонение оси рыскания и боковое смещение), задержка в четверть цикла между двумя движениями наделяет систему способностью извлекать энергию из поступательного движения. Этот эффект наблюдается при « флаттере » крыльев самолетов и « шимми » дорожных транспортных средств, а также при рыскании железнодорожных транспортных средств. Кинематическое решение, полученное выше, описывает движение на критической скорости.

На практике при скорости ниже критической задержка между двумя движениями составляет менее четверти цикла, так что движение затухает, но при скорости выше критической задержка составляет более четверти цикла, так что движение усиливается.

Для оценки инерционных сил необходимо выразить производные расстояния как производные времени . Это делается с использованием скорости транспортного средства U , которая предполагается постоянной:

${\displaystyle {\frac {\operatorname {d} }{\operatorname {d} t}}=U{\frac {\operatorname {d} }{\operatorname {d} x}}}$

Угловое ускорение оси по рысканию равно:

${\displaystyle {\frac {\operatorname {d} ^{2}\theta }{\operatorname {d} t^{2}}}=-U^{2}\left({\frac {2k}{rd}}\right)\theta }$

Инерционный момент (без учета гироскопических эффектов) равен:

${\displaystyle Fd=C{\frac {\operatorname {d} ^{2}\theta }{\operatorname {d} t^{2}}}}$

где F — сила, действующая вдоль рельсов, а C — момент инерции колесной пары.

${\displaystyle F=-CU^{2}\left({\frac {2k}{rd^{2}}}\right)\theta }$

максимальная сила трения между колесом и рельсом определяется по формуле:

${\displaystyle F=\mu {\frac {W}{2}}}$

где W — нагрузка на ось, а — коэффициент трения . Сильное проскальзывание произойдет при сочетании скорости и прогиба оси, определяемом как: ${\displaystyle \mu }$

${\displaystyle \theta U^{2}=\mu W{\frac {rd^{2}}{4Ck}}}$

Это выражение дает значительное завышение критической скорости, но оно иллюстрирует физическую причину, по которой происходит рысканье, т. е. силы инерции становятся сопоставимыми с силами адгезии выше определенной скорости. Предельное трение является плохим представлением силы адгезии в этом случае.

Фактические силы сцепления возникают из-за деформации протектора и рельса в области контакта. Нет грубого проскальзывания, есть только упругая деформация и некоторое локальное проскальзывание (проскальзывание ползучести). При нормальной работе эти силы находятся в пределах предельного ограничения трения. Полный анализ учитывает эти силы, используя теории механики контакта качения .

Однако кинематический анализ предполагал, что в контакте колеса с рельсом вообще нет проскальзывания. Теперь ясно, что есть некоторое проскальзывание, которое делает рассчитанную синусоидальную траекторию колесной пары (по формуле Клингеля) не совсем корректной.

Энергетический баланс

Чтобы получить оценку критической скорости, мы используем тот факт, что условие, при котором это кинематическое решение справедливо, соответствует случаю, когда нет чистого обмена энергией с окружающей средой, поэтому, рассматривая кинетическую и потенциальную энергию системы, мы должны иметь возможность вывести критическую скорость.

Позволять:

${\displaystyle \omega ={\frac {\operatorname {d} \theta }{\operatorname {d} t}}}$

Использование оператора:

${\displaystyle \omega {\frac {\operatorname {d} }{\operatorname {d} \theta }}={\frac {\operatorname {d} }{\operatorname {d} t}}}$

Уравнение углового ускорения можно выразить через угловую скорость по рысканию : ${\displaystyle \omega }$

${\displaystyle \omega {\frac {\operatorname {d} \omega }{\operatorname {d} \theta }}=-U^{2}\left({\frac {2k}{rd}}\right)\theta }$

интегрируя:

${\displaystyle {\frac {1}{2}}\omega ^{2}=-{\frac {1}{2}}U^{2}\left({\frac {2k}{rd}}\right)\theta ^{2}}$

поэтому кинетическая энергия вращения равна:

${\displaystyle {\frac {1}{2}}C\omega ^{2}=-{\frac {1}{2}}CU^{2}\left({\frac {2k}{rd}}\right)\theta ^{2}}$

Смещение точек контакта наружу при рыскании оси

Когда ось рыскает, точки контакта перемещаются наружу на ступенях, так что высота оси уменьшается. Расстояние между точками опоры увеличивается до:

${\displaystyle {\frac {d}{cos(\theta )}}=d\left(1+{\frac {1}{2}}\theta ^{2}\right)}$

(до второго порядка малости). смещение точки опоры от центров ступеней равно:

${\displaystyle {\frac {1}{2}}\left(d+{\frac {1}{2}}d\theta ^{2}-d\right)}$

нагрузка на ось падает на

${\displaystyle h={\frac {1}{4}}kd\theta ^{2}}$

Таким образом, работа, выполняемая за счет снижения нагрузки на ось, равна:

${\displaystyle E={\frac {1}{4}}Wkd\theta ^{2}}$

Это энергия, потерянная системой, поэтому для продолжения движения необходимо извлечь равное количество энергии из поступательного движения колесной пары.

Скорость внешнего колеса определяется по формуле:

${\displaystyle V={\frac {U}{r}}\left(r+ky\right)}$

Кинетическая энергия равна:

${\displaystyle {\frac {1}{4}}m\left(U^{2}+2U^{2}{\frac {ky}{r}}+U^{2}{\frac {k^{2}y^{2}}{r^{2}}}\right)}$

для внутреннего колеса это

${\displaystyle {\frac {1}{4}}m\left(U^{2}-2U^{2}{\frac {ky}{r}}+U^{2}{\frac {k^{2}y^{2}}{r^{2}}}\right)}$

где m — масса обоих колес.

Увеличение кинетической энергии равно:

${\displaystyle \delta E={\frac {1}{2}}m\left({\frac {Uky}{r}}\right)^{2}}$

Движение будет продолжаться с постоянной амплитудой до тех пор, пока энергия , извлекаемая из поступательного движения и проявляющаяся в увеличении кинетической энергии колесной пары при нулевом рыскании, не станет равна потенциальной энергии, потерянной из-за снижения нагрузки на ось при максимальном рыскании.

Теперь из кинематики:

${\displaystyle {\begin{aligned}2U{\frac {ky}{rd}}&=\omega \\\delta E&={\frac {1}{8}}md^{2}\omega ^{2}\end{aligned}}}$

но

${\displaystyle \omega ^{2}=-U^{2}\left({\frac {2k}{rd}}\right)\theta ^{2}}$

Поступательная кинетическая энергия равна

${\displaystyle \delta E=-{\frac {1}{8}}U^{2}md^{2}\left({\frac {2k}{rd}}\right)\theta ^{2}}$

Полная кинетическая энергия равна:

${\displaystyle T={\frac {1}{2}}U^{2}\left(C+{\frac {md^{2}}{4}}\right)\left({\frac {2k}{rd}}\right)\theta ^{2}}$

Критическая скорость находится из баланса энергии:

${\displaystyle {\frac {Wkd}{2}}=U^{2}{\frac {2k}{rd}}\left(C+{\frac {md^{2}}{4}}\right)}$

Следовательно, критическая скорость определяется выражением

${\displaystyle U^{2}={\frac {Wrd^{2}}{4C+md^{2}}}}$

Это не зависит от конусности колеса, но зависит от соотношения нагрузки на ось и массы колесной пары. Если бы протекторы были действительно коническими по форме, критическая скорость не зависела бы от конусности. На практике износ колеса приводит к изменению конусности по ширине протектора, так что значение конусности, используемое для определения потенциальной энергии, отличается от значения, используемого для расчета кинетической энергии. Обозначая первое как a , критическая скорость становится:

${\displaystyle U^{2}={\frac {Ward^{2}}{k(4C+md^{2})}}}$

где a теперь является коэффициентом формы, определяемым износом колеса . Этот результат получен в Wickens (1965) ^[9] из анализа динамики системы с использованием стандартных методов инженерного управления .

Ограничение упрощенного анализа

Движение колесной пары гораздо сложнее, чем показывает этот анализ. Существуют дополнительные сдерживающие силы, прикладываемые подвеской транспортного средства ^[10] , и на высокой скорости колесная пара будет генерировать дополнительные гироскопические моменты, которые изменят оценку критической скорости. Традиционно железнодорожное транспортное средство имеет устойчивое движение на низких скоростях, когда оно достигает высоких скоростей, устойчивость переходит в неустойчивую форму. Основная цель нелинейного анализа динамики системы рельсового транспортного средства - показать вид аналитического исследования бифуркации, нелинейной боковой устойчивости и поведения рыскания рельсовых транспортных средств на прямолинейном пути. В этом исследовании описывается метод Боголюбова для анализа. ^[11]

В исследованиях основное внимание уделяется двум основным вопросам, а именно, предположению, что кузов является неподвижной опорой, и влиянию нелинейных элементов при расчете скорости рыскания. ^[12] Реальное железнодорожное транспортное средство имеет гораздо больше степеней свободы и, следовательно, может иметь более одной критической скорости; совершенно не очевидно, что самая низкая скорость диктуется движением колесной пары. Однако анализ поучителен, поскольку он показывает, почему происходит рыскание. По мере увеличения скорости силы инерции становятся сопоставимыми с силами сцепления. Вот почему критическая скорость зависит от отношения нагрузки на ось (которая определяет силу сцепления) к массе колесной пары (которая определяет силы инерции).

В качестве альтернативы, ниже определенной скорости энергия, извлекаемая из поступательного движения, недостаточна для возмещения энергии, потерянной при опускании осей, и движение затухает; выше этой скорости извлекаемая энергия больше потери потенциальной энергии, и амплитуда нарастает.

Потенциальная энергия при максимальном рыскании оси может быть увеличена путем включения упругого ограничения на рыскание оси, так что есть вклад, возникающий из-за натяжения пружины. Расположение колес в тележках для увеличения ограничения на рыскание колесных пар и применение упругих ограничений к тележке также повышает критическую скорость. Введение упругих сил в уравнение позволяет использовать конструкции подвески, которые ограничены только началом грубого проскальзывания, а не классическим рысканием. Штрафом за фактическое устранение рыскания является прямая колея с сопутствующей проблемой преимущественного проезда и несовместимостью с устаревшей инфраструктурой.

Hunting — это динамическая проблема, которая может быть решена, по крайней мере, в принципе, с помощью активного управления с обратной связью, которое может быть адаптировано к качеству пути. Однако внедрение активного управления поднимает вопросы надежности и безопасности.

Вскоре после начала виляния происходит сильное проскальзывание, и реборды колес ударяются о рельсы, что может привести к повреждению обоих.

Дорожно-рельсовые транспортные средства

Независимые оси рельсовых колес широко распространены на железнодорожного транспорта.

Многие дорожные и рельсовые транспортные средства имеют независимые оси и подвески на каждом рельсовом колесе. Когда это сочетается с наличием дорожных колес на рельсе, становится трудно использовать приведенные выше формулы. Исторически сложилось так, что дорожные и рельсовые транспортные средства имеют передние колеса, установленные слегка под углом схождения , что, как было обнаружено, минимизирует виляние во время движения транспортного средства по рельсам.

Смотрите также

• Механика фрикционного контакта
• Сцепление с рельсами
• Профиль рельса
• Колебание скорости
• Динамика автомобиля
• Колесная пара

Общие методы решения этого класса задач см.

• Контрольная техника

Ссылки

1. Oxford English Dictionary (2-е изд.). Oxford University Press. 1989. f. Действие машины, прибора, системы и т. п., представляющее собой охоту (см. охота, т. 7б); нежелательное колебание относительно равновесной скорости, положения или состояния.
2. https://www.talgo.com/en/rolling-stock/very-high-speed/350/
3. Ошибка слежения будет равна нулю, если путь колес проходит абсолютно прямолинейно по рельсам, а колесная пара находится по центру рельсов.
4. См. Curvature#Graph функции для математических подробностей. Приблизительное равенство становится равенством только тогда, когда ошибка отслеживания y имеет нулевой наклон относительно x . Поскольку ошибка отслеживания окажется синусоидой, точки нулевого наклона находятся в точках максимальной ошибки отслеживания y . Но равенство приблизительно верно, если наклон y мал.
5. Обратите внимание, что отрицательно, когда y положительно, и наоборот. Другое уравнение для R не выполняется, когда y становится отрицательным, поскольку радиус R не может быть отрицательным (согласно математическому определению). Но после того, как радиус R исключается путем объединения двух уравнений, результирующее уравнение становится правильным, если проверить два случая: y отрицательно и y положительно. ${\displaystyle {\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}}$ ${\displaystyle {\frac {1}{R}}={\frac {2ky}{rd}}}$
6. Ивницкий, стр.7 формула 2.1
7. Картер, Ф. У. (25 июля 1928 г.). «О стабильности движения локомотивов». Труды Королевского общества . 121 (788): 585–610. Bibcode : 1928RSPSA.121..585C. doi : 10.1098/rspa.1928.0220 .
8. Knothe, K. (2008). «История механики контакта колеса/рельса: от Редтенбахера до Калькера». Vehicle System Dynamics . 46 (1–2): 9–26. doi :10.1080/00423110701586469. S2CID  109580328.
9. Wickens, AH (1965–66). «Динамика железнодорожных транспортных средств на прямом пути: фундаментальные соображения о поперечной устойчивости». Труды Института инженеров-механиков : 29–.
10. Wickens, AH; Gilchrist, AO; Hobbs, AEW (1969–70). «Проект подвески для высокопроизводительных двухосных грузовых транспортных средств». Труды Института инженеров-механиков : 22–.
11. Сераджян, Реза (2013). «Влияние изменения параметров при различной боковой жесткости на нелинейный анализ поведения тележки при рыскании». Журнал измерений в машиностроении : 195–206.
12. Сераджян, Реза (2011). «Влияние инерции тележки и кузова на нелинейные колебания колесной пары, распознаваемые теорией бифуркации Хопфа». Int J Auto Engng : 186–196.

• Ивницкий, Саймон (2006). Справочник по динамике железнодорожного транспорта . CRC Press.
• Шабана, Ахмед А. и др. (2008). Динамика железнодорожного транспорта: вычислительный подход . CRC Press.
• Wickens, AH (1 января 2003 г.). Основы динамики рельсовых транспортных средств: управление и боковая устойчивость . Swets & Zeitlinger.
• Сераджян, Реза (2013). Влияние изменения параметров при различной боковой жесткости на нелинейный анализ поведения тележки при рыскании . CRC Press.
• Сераджян, Реза (2011). Влияние инерции тележки и кузова на нелинейные колебания колесной пары, распознаваемые теорией бифуркации Хопфа . CRC Press.