Цент — логарифмическая единица измерения музыкальных интервалов . Двенадцатитоновая равномерная темперация делит октаву на 12 полутонов по 100 центов каждый. Обычно центы используются для выражения небольших интервалов, для проверки интонации или для сравнения размеров сопоставимых интервалов в разных системах настройки . Для людей один цент слишком мал, чтобы восприниматься между последовательными нотами.
Центы, как их описал Александр Джон Эллис , следуют традиции измерения интервалов логарифмами , которая началась с Хуана Карамуэля и Лобковица в 17 веке. [a] Эллис решил основывать свои меры на сотой части полутона, 1200 √ 2 , по предложению Роберта Холфорда Макдауэлла Бозанкета . Проводя обширные измерения музыкальных инструментов по всему миру, Эллис использовал центы для отчета и сравнения используемых гамм, [1] и далее описал и использовал эту систему в своем издании 1875 года « О ощущениях тона » Германа фон Гельмгольца . Это стало стандартным методом представления и сравнения музыкальных высот и интервалов. [2] [3]
В статье Александра Джона Эллиса «О музыкальных гаммах различных наций » [1], опубликованной в журнале «Journal of the Society of Arts» в 1885 году, официально была введена система центов, которая должна была использоваться при исследовании музыкальных гамм различных наций путем сравнения и сопоставления. Система центов уже была определена в его «Истории музыкального тона» , где Эллис пишет: «Если бы мы предположили, что между каждой парой соседних нот, образующих равный полутон [...], было бы вставлено 99 других нот, создающих точно равные интервалы друг с другом, мы должны были бы разделить октаву на 1200 равных сотых [ sic ] равного полутона, или центов , как их можно кратко назвать». [4]
Эллис определил высоту музыкальной ноты в своей работе 1880 года «История музыкальной высоты» [5] как «количество двойных или полных колебаний вперед и назад, совершаемых в каждую секунду частицей воздуха, пока слышна нота». [6] Позднее он определил музыкальную высоту как «высоту тона или V [для «двойных колебаний»] любой названной музыкальной ноты, которая определяет высоту всех других нот в определенной системе настроек». [7] Он отмечает, что эти ноты, когда звучат последовательно, образуют гамму инструмента, а интервал между любыми двумя нотами измеряется «отношением меньшего номера высоты к большему или дробью, образованной делением большего на меньшее». [8] Абсолютная и относительная высота тона также определялись на основе этих соотношений. [8]
Эллис отметил, что «цель настройщика — сделать интервал [...] между любыми двумя нотами, соответствующими любым двум соседним клавишам пальцев по всему инструменту, совершенно одинаковым. Результат называется равномерной темперацией или настройкой, и это система, которая в настоящее время используется по всей Европе. [9] Далее он приводит расчеты для приблизительной меры отношения в центах, добавляя, что «как правило, нет необходимости выходить за пределы ближайшего целого числа центов». [10]
Эллис представляет применение системы центов в этой статье на музыкальных гаммах разных народов, которые включают: (I. Гептатонные гаммы) Древняя Греция и Современная Европа, [11] Персия, Аравия, Сирия и Шотландское нагорье, [12] Индия, [13] Сингапур, [14] Бирма [15] и Сиам; [16] (II. Пентатонические гаммы) Южная часть Тихого океана, [17] Западная Африка, [18] Ява, [19] Китай [20] и Япония. [21] И он приходит к выводу, что «Музыкальная гамма не является единой, не является «естественной» и даже не основана обязательно на законах строения музыкального звука, так прекрасно разработанных Гельмгольцем, а очень разнообразна, очень искусственна и очень капризна». [22]
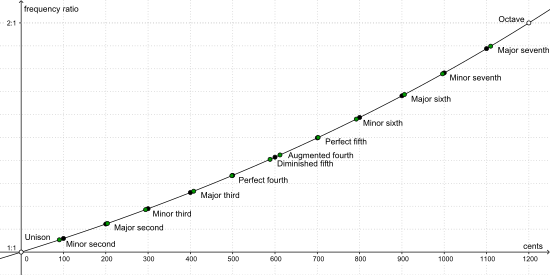
Цент — это единица измерения соотношения двух частот. Равномерно темперированный полутон (интервал между двумя соседними клавишами фортепиано) по определению охватывает 100 центов. Октава — две ноты с соотношением частот 2:1 — охватывает двенадцать полутонов и, следовательно, 1200 центов. Соотношение частот, отстоящих друг от друга на один цент, точно равно 2 1 ⁄ 1200 = 1200 √ 2 , корень 1200-й степени из 2, что приблизительно равно1.000 577 7895 . Таким образом, повышение частоты на один цент соответствует умножению исходной частоты на это постоянное значение. Повышение частоты на 1200 центов удваивает частоту, что приводит к ее октаве.
Если известны частоты и двух нот, то число центов, измеряющих интервал от до, равно:
Аналогично, если известно и количество центов в интервале от до , то равно:
Большая терция в простом интонировании имеет частотное соотношение 5:4 или ~386 центов, но в равномерной темперации составляет 400 центов. Эта разница в 14 центов составляет примерно седьмую часть полутона и достаточно велика, чтобы быть слышимой.
При увеличении x от 0 до 1 ⁄ 12 функция 2 x возрастает почти линейно от1.000 00 к1,059 46 , что позволяет использовать кусочно-линейную аппроксимацию . Таким образом, хотя центы представляют логарифмическую шкалу, небольшие интервалы (менее 100 центов) можно приблизительно аппроксимировать линейным соотношением 1 + 0,000 5946 вместо истинной экспоненциальной зависимости 2 c ⁄ 1200 . Округленная ошибка равна нулю, когда 0 или 100, и составляет всего около 0,72 цента при = 50 (чье правильное значение 2 1 ⁄ 24 ≅ 1,029 30 приблизительно равно 1 + 0,000 5946 × 50 ≅ 1,02973). Эта ошибка значительно ниже любой слышимой человеком погрешности, что делает эту кусочно-линейную аппроксимацию подходящей для большинства практических целей.
Трудно установить, сколько центов воспринимаются людьми; эта точность сильно варьируется от человека к человеку. Один автор заявил, что люди могут различать разницу в высоте тона около 5–6 центов. [23] Порог того, что воспринимается, технически известный как едва заметная разница (JND), также варьируется в зависимости от частоты, амплитуды и тембра . В одном исследовании изменения в качестве тона снизили способность студентов-музыкантов распознавать как несоответствующие тональности, которые отклонялись от своих соответствующих значений на ±12 центов. [24] Также было установлено, что увеличенный тональный контекст позволяет слушателям точнее судить о высоте тона. [25] «В то время как интервалы менее нескольких центов незаметны для человеческого уха в мелодическом контексте, в гармонии очень небольшие изменения могут вызвать большие изменения в ритме и грубости аккордов». [26]
При прослушивании высоты звука с вибрато есть доказательства того, что люди воспринимают среднюю частоту как центр высоты звука. [27] Одно исследование современных исполнений « Ave Maria» Шуберта обнаружило, что диапазон вибрато обычно варьировался от ±34 центов до ±123 центов со средним значением ±71 цент, а также отметило более высокую вариативность в оперных ариях Верди . [28]
Нормальные взрослые способны очень надежно распознавать разницу в высоте звука размером до 25 центов. Однако взрослые с амузией испытывают трудности с распознаванием разницы менее 100 центов, а иногда и с этими или большими интервалами. [29]
Представление музыкальных интервалов логарифмами почти так же старо, как и сами логарифмы. Логарифмы были изобретены лордом Нейпиром в 1614 году. [30] Еще в 1647 году Хуан Карамуэль и Лобковиц (1606-1682) в письме к Атанасиусу Кирхеру описал использование логарифмов с основанием 2 в музыке. [31] В этом основании октава представлена как 1, полутон как 1/12 и т. д.
Joseph Sauveur в своих Principes d'acoustique et de musique 1701 года предложил использовать логарифмы с основанием 10, вероятно, потому, что были доступны таблицы. Он использовал логарифмы, вычисленные с тремя десятичными знаками. Логарифм с основанием 10 от 2 равен приблизительно 0,301, который Sauveur умножает на 1000, чтобы получить 301 единицу в октаве. Чтобы работать с более управляемыми единицами, он предлагает взять 7/301, чтобы получить единицы 1/43 октавы. [b] Таким образом, октава делится на 43 части, называемые «меридами», которые в свою очередь делятся на 7 частей, «гептамеридами». Sauveur также представлял себе возможность дальнейшего деления каждой гептамериды на 10, но на самом деле не использует такие микроскопические единицы. [32]
Феликс Савар (1791-1841) перенял систему Совера, не ограничивая количество десятичных знаков логарифма 2, так что значение его единицы варьируется в зависимости от источников. С пятью десятичными знаками десятичный логарифм 2 равен 0,30103, что дает 301,03 савара в октаве. [33] Это значение часто округляется до 1/301 или до 1/300 октавы. [34] [35]
В начале 19 века Гаспар де Прони предложил логарифмическую единицу основания , где единица соответствует полутону в равномерной темперации. [36] Александр Джон Эллис в 1880 году описывает большое количество стандартов высоты тона, которые он записал или вычислил, указывая в прони с двумя десятичными знаками, т.е. с точностью до 1/100 полутона, [37] интервал, который отделял их от теоретической высоты тона в 370 Гц, взятой за точку отсчета. [38]
Сантитон (также Иринг ) — музыкальный интервал (2 1 ⁄ 600 ) , равный двум центам (2 2 ⁄ 1200 ) [ 39] [40], предложенный в качестве единицы измерения ( ) Видогастом Ирингом в работе «Die reine Stimmung in der Musik» (1898) как 600 шагов на октаву , а позднее Йозефом Яссером в работе «Теория эволюционирующей тональности» (1932) как 100 шагов на равномерно темперированный целый тон .
Иринг заметил, что град/веркмейстер (1,96 цента, 12 на пифагорейскую комму ) и схизма (1,95 цента) почти одинаковы (≈ 614 шагов на октаву), и оба могут быть приближены к 600 шагам на октаву (2 цента). [41] Яссер продвигал децитон , сантитон и миллитон (10, 100 и 1000 шагов на целый тон = 60, 600 и 6000 шагов на октаву = 20, 2 и 0,2 цента). [42] [43]
Например: Равномерно темперированная чистая квинта = 700 центов = 175,6 савара = 583,3 миллиоктавы = 350 сантитонов. [44]
Следующие аудиофайлы воспроизводят различные интервалы. В каждом случае первая нота — это средняя C. Следующая нота выше C на назначенное значение в центах. Наконец, обе ноты воспроизводятся одновременно.
Обратите внимание, что JND для разницы в высоте составляет 5–6 центов. При игре по отдельности ноты могут не показывать слышимой разницы, но при игре вместе может быть слышно биение (например, если сыграны нота C и нота на 10 центов выше). В любой конкретный момент две формы волны усиливают или нейтрализуют друг друга в большей или меньшей степени, в зависимости от их мгновенного фазового соотношения. Настройщик фортепиано может проверить точность настройки, определяя время биения, когда две струны звучат одновременно.
, частота ударов = 0,16Гц
, частота ударов = 1,53 Гц
, частота ударов = 3,81 Гц
![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)
![{\displaystyle {\sqrt[{600}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea43c0bc8f62081f2f0b830dd7da893a9d97a9a9)
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )Интервальные пропорции можно преобразовать в центовые значения, которые сегодня широко используются.
{{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )