
В физике столкновение — это любое событие , в котором два или более тел оказывают друг на друга силы в течение относительно короткого времени. Хотя наиболее распространенное использование слова столкновение относится к инцидентам, в которых два или более объектов сталкиваются с большой силой, научное использование этого термина ничего не подразумевает о величине силы. [1]
Столкновение — это кратковременное взаимодействие между двумя телами или более чем двумя телами одновременно, вызывающее изменение движения вовлеченных тел из-за внутренних сил, действующих между ними во время этого. Столкновения включают силы (имеется изменение скорости ). Величина разницы скоростей непосредственно перед ударом называется скоростью сближения . Все столкновения сохраняют импульс . Различие между типами столкновений заключается в том, сохраняют ли они также кинетическую энергию системы до и после столкновения. Столкновения бывают трех типов:
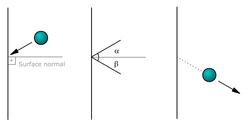
Степень упругости или неупругости столкновения количественно определяется коэффициентом восстановления , значение которого обычно находится в диапазоне от нуля до единицы. Совершенно упругое столкновение имеет коэффициент восстановления, равный единице; совершенно неупругое столкновение имеет коэффициент восстановления, равный нулю. Линия удара — это линия, которая коллинеарна общей нормали поверхностей, которые находятся ближе всего или соприкасаются во время удара. Это линия, вдоль которой действует внутренняя сила столкновения во время удара, и коэффициент восстановления Ньютона определяется только вдоль этой линии.
Столкновения в идеальных газах приближаются к абсолютно упругим столкновениям, как и рассеивающие взаимодействия субатомных частиц , которые отклоняются электромагнитной силой . Некоторые крупномасштабные взаимодействия, такие как гравитационные взаимодействия типа рогатки между спутниками и планетами, являются почти идеально упругими.
Столкновения играют важную роль в бильярдном спорте . Поскольку столкновения между бильярдными шарами почти упругие , а шары катятся по поверхности, которая создает низкое трение качения , их поведение часто используется для иллюстрации законов движения Ньютона . После столкновения без трения движущегося шара с неподвижным шаром такой же массы угол между направлениями двух шаров составляет 90 градусов. Это важный факт, который учитывают профессиональные игроки в бильярд [2], хотя он предполагает, что шар движется без какого-либо воздействия трения по столу, а не катится с трением. Рассмотрим упругое столкновение в двух измерениях любых двух масс m 1 и m 2 с соответствующими начальными скоростями u 1 и u 2, где u 2 = 0 , и конечными скоростями V 1 и V 2. Сохранение импульса дает m 1 u 1 = m 1 V 1 + m 2 V 2 . Сохранение энергии для упругого столкновения дает (1/2) m 1 | u 1 | 2 = (1/2) m 1 | V 1 | 2 + (1/2) m 2 | V 2 | 2 . Теперь рассмотрим случай m 1 = m 2 : получаем u 1 = V 1 + V 2 и | u 1 | 2 = | V 1 | 2 + | V 2 | 2 . Взяв скалярное произведение каждой стороны первого уравнения на себя, | u 1 | 2 = u 1 • u 1 = | V 1 | 2 + | V 2 | 2 + 2 V 1 • V 2 . Сравнивая это со вторым уравнением, получаем V 1 • V 2= 0, поэтому они перпендикулярны, если только V 1 не является нулевым вектором (что происходит тогда и только тогда, когда столкновение происходит лоб в лоб).
При совершенно неупругом столкновении , т.е. при нулевом коэффициенте восстановления , сталкивающиеся частицы сливаются . Необходимо учитывать закон сохранения импульса:
где v — конечная скорость, которая, следовательно, определяется выражением
Уменьшение полной кинетической энергии равно полной кинетической энергии до столкновения в системе отсчета центра импульса относительно системы из двух частиц, потому что в такой системе отсчета кинетическая энергия после столкновения равна нулю. В этой системе отсчета большая часть кинетической энергии до столкновения принадлежит частице с меньшей массой. В другой системе отсчета, в дополнение к уменьшению кинетической энергии, может происходить передача кинетической энергии от одной частицы к другой; тот факт, что это зависит от системы отсчета, показывает, насколько это относительно. При обратном времени мы имеем ситуацию двух объектов, отталкивающихся друг от друга, например, выстрел снарядом или ракетой, применяющей тягу (сравните вывод уравнения ракеты Циолковского ).
Столкновения стопы или лапы животного с подстилающим субстратом обычно называются силами реакции грунта. Эти столкновения неупругие, поскольку кинетическая энергия не сохраняется. Важной темой исследований в области протезирования является количественная оценка сил, возникающих во время столкновений стопы с грунтом, связанных как с инвалидной, так и с неинвалидной походкой. Такая количественная оценка обычно требует, чтобы субъекты шли по силовой платформе (иногда называемой «силовой пластиной»), а также детального кинематического и динамического (иногда называемого кинетическим) анализа.
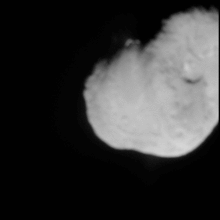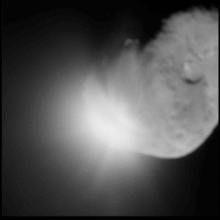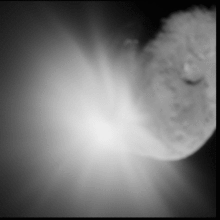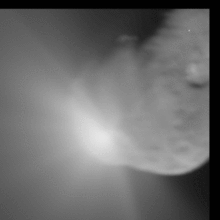
Гиперскорость — очень высокая скорость , приблизительно более 3000 метров в секунду (11 000 км/ч, 6700 миль/ч, 10 000 футов/с или 8,8 Маха ). В частности, гиперскорость — это скорость настолько высокая, что прочность материалов при ударе очень мала по сравнению с инерционными напряжениями. [3] Таким образом, металлы и жидкости ведут себя одинаково при ударе на гиперскорости. Удар при экстремальной гиперскорости приводит к испарению ударника и цели. Для конструкционных металлов гиперскорость обычно считается более 2500 м/с (5600 миль/ч, 9000 км/ч, 8200 футов/с или 7,3 Маха). Метеоритные кратеры также являются примерами ударов на гиперскорости.