Теория молекулярных орбиталей

Метод описания электронной структуры молекул с помощью квантовой механики

В химии теория молекулярных орбиталей (теория МО или МОД) — это метод описания электронной структуры молекул с использованием квантовой механики . Она была предложена в начале 20-го века. МОД объясняет парамагнитную природу O 2 , которую теория валентных связей объяснить не может.

В теории молекулярных орбиталей электроны в молекуле не приписываются к отдельным химическим связям между атомами , а рассматриваются как движущиеся под влиянием атомных ядер во всей молекуле. ^[1] Квантовая механика описывает пространственные и энергетические свойства электронов как молекулярных орбиталей, которые окружают два или более атомов в молекуле и содержат валентные электроны между атомами.

Теория молекулярных орбиталей произвела революцию в изучении химических связей, аппроксимируя состояния связанных электронов – молекулярных орбиталей – как линейные комбинации атомных орбиталей (ЛКАО). Эти аппроксимации производятся путем применения теории функционала плотности (DFT) или моделей Хартри-Фока (HF) к уравнению Шредингера .

Теория молекулярных орбиталей и теория валентных связей являются основополагающими теориями квантовой химии .

Метод линейной комбинации атомных орбиталей (ЛКАО)

В методе LCAO каждая молекула имеет набор молекулярных орбиталей . Предполагается, что волновая функция молекулярной орбитали ψ _j может быть записана как простая взвешенная сумма n составляющих атомных орбиталей χ _i , согласно следующему уравнению: ^[2]

$${\displaystyle \psi _{j}=\sum _{i=1}^{n}c_{ij}\chi _{i}.}$$

Коэффициенты c _ij можно определить численно, подставив это уравнение в уравнение Шредингера и применив вариационный принцип . Вариационный принцип — это математический метод, используемый в квантовой механике для построения коэффициентов каждого атомного орбитального базиса. Больший коэффициент означает, что орбитальный базис состоит в большей степени из этой конкретной вносящей вклад атомной орбитали — следовательно, молекулярная орбиталь лучше всего характеризуется этим типом. Этот метод количественной оценки орбитального вклада как линейной комбинации атомных орбиталей используется в вычислительной химии . Дополнительное унитарное преобразование может быть применено к системе для ускорения сходимости в некоторых вычислительных схемах. Теория молекулярных орбиталей рассматривалась как конкурент теории валентных связей в 1930-х годах, прежде чем стало понятно, что эти два метода тесно связаны и что при расширении они становятся эквивалентными.

Теория молекулярных орбиталей используется для интерпретации ультрафиолетово-видимой спектроскопии (UV–VIS). Изменения в электронной структуре молекул можно увидеть по поглощению света на определенных длинах волн. Можно сделать назначения этим сигналам, указанным переходом электронов, движущихся с одной орбитали с более низкой энергией на орбиталь с более высокой энергией. Диаграмма молекулярных орбиталей для конечного состояния описывает электронную природу молекулы в возбужденном состоянии.

Существуют три основных требования к комбинациям атомных орбиталей, чтобы их можно было использовать в качестве приблизительных молекулярных орбиталей.

1. Атомная орбитальная комбинация должна иметь правильную симметрию, что означает, что она должна принадлежать к правильному неприводимому представлению молекулярной группы симметрии . Используя адаптированные к симметрии линейные комбинации , или SALC, можно сформировать молекулярные орбитали правильной симметрии.
2. Атомные орбитали также должны перекрываться в пространстве. Они не могут объединиться, чтобы сформировать молекулярные орбитали, если они находятся слишком далеко друг от друга.
3. Атомные орбитали должны находиться на схожих энергетических уровнях, чтобы объединиться в молекулярные орбитали. Потому что если разница в энергии велика, то при образовании молекулярных орбиталей изменение энергии становится небольшим. Следовательно, недостаточного снижения энергии электронов для создания существенной связи не происходит. ^[3]

История

Теория молекулярных орбиталей была разработана в годы после создания теории валентных связей (1927), в первую очередь благодаря усилиям Фридриха Хунда , Роберта Малликена , Джона К. Слейтера и Джона Леннарда-Джонса . ^[4] Теория МО изначально называлась теорией Хунда-Малликена. ^[5] По словам физика и физического химика Эриха Хюккеля , первым количественным использованием теории молекулярных орбиталей была работа Леннарда-Джонса 1929 года . ^{[6] [7]} В этой статье было предсказано триплетное основное состояние для молекулы дикислорода , что объясняло ее парамагнетизм ^[8] (см. диаграмму молекулярных орбиталей § Дикислород ) до теории валентных связей, которая предложила свое собственное объяснение в 1931 году. ^[9] Слово «орбиталь» было введено Малликеном в 1932 году. ^[5] К 1933 году теория молекулярных орбиталей была принята как обоснованная и полезная теория. ^[10]

Эрих Хюккель применил теорию молекулярных орбиталей к ненасыщенным молекулам углеводородов, начав в 1931 году с его метода молекулярных орбиталей Хюккеля (HMO) для определения энергий МО для пи-электронов , который он применил к сопряженным и ароматическим углеводородам. ^{[11] [12]} Этот метод дал объяснение стабильности молекул с шестью пи-электронами, таких как бензол .

Первый точный расчет волновой функции молекулярной орбитали был сделан Чарльзом Коулсоном в 1938 году на молекуле водорода. ^[13] К 1950 году молекулярные орбитали были полностью определены как собственные функции (волновые функции) самосогласованного гамильтониана поля , и именно в этот момент теория молекулярных орбиталей стала полностью строгой и последовательной. ^[14] Этот строгий подход известен как метод Хартри-Фока для молекул, хотя он имел свои истоки в расчетах на атомах. В расчетах на молекулах молекулярные орбитали расширяются в терминах атомного орбитального базисного набора , что приводит к уравнениям Рутана . ^[15] Это привело к разработке многих методов квантовой химии ab initio . Параллельно с этим теория молекулярных орбиталей применялась более приближенным образом с использованием некоторых эмпирически полученных параметров в методах, которые теперь известны как полуэмпирические методы квантовой химии . ^[15]

Успех теории молекулярных орбиталей также породил теорию лигандного поля , которая была разработана в 1930-х и 1940-х годах как альтернатива теории кристаллического поля .

Типы орбиталей

Диаграмма МО, показывающая образование молекулярных орбиталей H ₂ (в центре) из атомных орбиталей двух атомов H. МО с более низкой энергией связывает с электронной плотностью, сосредоточенной между двумя ядрами H. МО с более высокой энергией разрыхляет с электронной плотностью, сосредоточенной позади каждого ядра H.

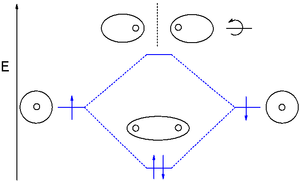
Теория молекулярных орбиталей (МО) использует линейную комбинацию атомных орбиталей (ЛКАО) для представления молекулярных орбиталей, возникающих в результате связей между атомами. Их часто делят на три типа: связывающие , антисвязывающие и несвязывающие . Связывающая орбиталь концентрирует электронную плотность в области между заданной парой атомов, так что ее электронная плотность будет стремиться притягивать каждое из двух ядер к другому и удерживать два атома вместе. ^[16] Антисвязывающая орбиталь концентрирует электронную плотность «позади» каждого ядра (т. е. на стороне каждого атома, которая наиболее удалена от другого атома), и поэтому стремится оттянуть каждое из двух ядер друг от друга и фактически ослабить связь между двумя ядрами. Электроны на несвязывающих орбиталях, как правило, связаны с атомными орбиталями, которые не взаимодействуют друг с другом положительно или отрицательно, и электроны на этих орбиталях не способствуют и не уменьшают прочность связи. ^[16]

Молекулярные орбитали далее подразделяются в соответствии с типами атомных орбиталей, из которых они образованы. Химические вещества будут образовывать связывающие взаимодействия, если их орбитали станут ниже по энергии, когда они взаимодействуют друг с другом. Различают различные связывающие орбитали, которые отличаются электронной конфигурацией (формой электронного облака) и уровнями энергии .

Молекулярные орбитали молекулы можно проиллюстрировать на диаграммах молекулярных орбиталей .

Обычными связывающими орбиталями являются сигма (σ)-орбитали , которые симметричны относительно оси связи, и пи (π)-орбитали с узловой плоскостью вдоль оси связи. Менее распространенными являются дельта (δ)-орбитали и фи (φ)-орбитали с двумя и тремя узловыми плоскостями соответственно вдоль оси связи. Разрыхляющие орбитали обозначаются добавлением звездочки. Например, разрыхляющая пи-орбиталь может быть обозначена как π*.

Заказ на облигации

Молекулярная орбитальная диаграмма He ₂

Порядок связи — это число химических связей между парой атомов. Порядок связи молекулы можно рассчитать, вычитая число электронов на антисвязывающих орбиталях из числа связывающих орбиталей, а затем полученное число делится на два. Ожидается, что молекула будет стабильной, если ее порядок связи больше нуля. Достаточно рассмотреть валентный электрон , чтобы определить порядок связи. Поскольку (для главного квантового числа n > 1), когда МО выводятся из 1s AO, разница в числе электронов на связывающей и антисвязывающей молекулярной орбитали равна нулю. Таким образом, нет никакого чистого эффекта на порядок связи, если электрон не является валентным.

${\displaystyle {\text{Bond order}}={\frac {1}{2}}({\text{Number of electrons in bonding MO}}-{\text{Number of electrons in anti-bonding MO}})}$

Из порядка связи можно предсказать, образуется ли связь между двумя атомами или нет. Например, существование молекулы He _2. Из молекулярной орбитальной диаграммы порядок связи равен . Это означает, что между двумя атомами He не произойдет образования связи, что наблюдается экспериментально. Это можно обнаружить при очень низкой температуре и давлении молекулярного пучка, и его энергия связи составляет приблизительно 0,001 Дж/моль. ^[17] ${\textstyle {\frac {1}{2}}(2-2)=0}$

Кроме того, прочность связи может быть также реализована из порядка связи (BO). Например:

Для H ₂ : порядок связи равен ; энергия связи равна 436 кДж/моль. ${\textstyle {\frac {1}{2}}(2-0)=1}$

Для H ₂ ⁺ : порядок связи равен ; энергия связи равна 171 кДж/моль. ${\textstyle {\frac {1}{2}}(1-0)={\frac {1}{2}}}$

Поскольку порядок связи H ²⁺ _меньше , чем у H ₂ , он должен быть менее стабильным, что наблюдается экспериментально и может быть видно из энергии связи.

Обзор

MOT обеспечивает глобальную, делокализованную перспективу химической связи . В теории MO любой электрон в молекуле может быть найден в любом месте молекулы, поскольку квантовые условия позволяют электронам перемещаться под влиянием произвольно большого числа ядер, пока они находятся в собственных состояниях, разрешенных определенными квантовыми правилами. Таким образом, при возбуждении необходимым количеством энергии посредством высокочастотного света или другими способами электроны могут переходить на молекулярные орбитали с более высокой энергией. Например, в простом случае двухатомной молекулы водорода продвижение одного электрона со связующей орбитали на антисвязывающую орбиталь может происходить под действием УФ-излучения. Это продвижение ослабляет связь между двумя атомами водорода и может привести к фотодиссоциации, разрыву химической связи из-за поглощения света.

Теория молекулярных орбиталей используется для интерпретации ультрафиолетово-видимой спектроскопии (UV–VIS). Изменения в электронной структуре молекул можно увидеть по поглощению света на определенных длинах волн. Можно сделать назначения этим сигналам, указанным переходом электронов, движущихся с одной орбитали с более низкой энергией на орбиталь с более высокой энергией. Диаграмма молекулярных орбиталей для конечного состояния описывает электронную природу молекулы в возбужденном состоянии.

Хотя в теории МО некоторые молекулярные орбитали могут удерживать электроны, которые более локализованы между определенными парами молекулярных атомов, другие орбитали могут удерживать электроны, которые распределены более равномерно по молекуле. Таким образом, в целом, связывание гораздо более делокализовано в теории МО, что делает ее более применимой к резонансным молекулам, которые имеют эквивалентные нецелочисленные порядки связей, чем теория валентных связей . Это делает теорию МО более полезной для описания расширенных систем.

Роберт С. Малликен , который активно участвовал в создании теории молекулярных орбиталей, считает каждую молекулу самодостаточной единицей. Он утверждает в своей статье:

...Попытки рассматривать молекулу как состоящую из определенных атомных или ионных единиц, удерживаемых вместе дискретным числом связывающих электронов или электронных пар, считаются более или менее бессмысленными, за исключением приближения в особых случаях или метода расчета […]. Молекула здесь рассматривается как набор ядер, вокруг каждого из которых сгруппирована электронная конфигурация, очень похожая на конфигурацию свободного атома во внешнем поле, за исключением того, что внешние части электронных конфигураций, окружающих каждое ядро, обычно принадлежат, частично, совместно двум или более ядрам.... ^[18]

Примером может служить описание МО бензола , C
₆ЧАС
₆, представляющий собой ароматическое гексагональное кольцо из шести атомов углерода и трех двойных связей. В этой молекуле 24 из 30 валентных связывающих электронов — 24 из атомов углерода и 6 из атомов водорода — расположены на 12 σ (сигма) связывающих орбиталях, которые в основном расположены между парами атомов (C–C или C–H), аналогично электронам в описании валентной связи. Однако в бензоле оставшиеся шесть связывающих электронов расположены на трех π (пи) молекулярных связывающих орбиталях, которые делокализованы вокруг кольца. Два из этих электронов находятся в МО, которая имеет равные орбитальные вклады от всех шести атомов. Остальные четыре электрона находятся на орбиталях с вертикальными узлами под прямым углом друг к другу. Как и в теории ВС, все эти шесть делокализованных π-электронов находятся в большем пространстве, которое существует выше и ниже плоскости кольца. Все связи углерод-углерод в бензоле химически эквивалентны. В теории МО это является прямым следствием того факта, что три молекулярные π-орбитали объединяются и равномерно распределяют дополнительные шесть электронов по шести атомам углерода.

Строение бензола

В молекулах, таких как метан , CH
₄, восемь валентных электронов находятся в четырех МО, которые распределены по всем пяти атомам. Можно преобразовать МО в четыре локализованные sp ³ -орбитали. Лайнус Полинг в 1931 году гибридизовал углеродные 2s- и 2p-орбитали так, чтобы они указывали непосредственно на базисные функции водорода 1s и имели максимальное перекрытие. Однако описание делокализованных МО больше подходит для прогнозирования энергий ионизации и положений спектральных полос поглощения . Когда метан ионизируется, из валентных МО берется один электрон, который может исходить из s-связи или трижды вырожденных уровней p-связи, что дает две энергии ионизации. Для сравнения, объяснение в теории валентных связей более сложное. Когда один электрон удаляется из sp ³ -орбитали, резонанс вызывается между четырьмя структурами валентных связей, каждая из которых имеет одну одноэлектронную связь и три двухэлектронные связи. Трижды вырожденные ионизированные состояния T ₂ и A _{1 (CH 4} ⁺ ) производятся из различных линейных комбинаций этих четырех структур. Разница в энергии между ионизированным и основным состоянием дает две энергии ионизации.

Как и в бензоле, в таких веществах, как бета-каротин , хлорофилл или гем , некоторые электроны на π-орбиталях разбросаны по молекулярным орбиталям на большие расстояния в молекуле, что приводит к поглощению света в области более низких энергий ( видимый спектр ), что объясняет характерные цвета этих веществ. ^[19] Эти и другие спектроскопические данные для молекул хорошо объясняются в теории МО, с акцентом на электронные состояния, связанные с многоцентровыми орбиталями, включая смешивание орбиталей, основанное на принципах соответствия орбитальной симметрии. ^[16] Те же принципы МО также естественным образом объясняют некоторые электрические явления, такие как высокая электропроводность в плоскостном направлении гексагональных атомных листов, которые существуют в графите . Это является результатом непрерывного перекрытия полос наполовину заполненных p-орбиталей и объясняет электропроводность. Теория МО признает, что некоторые электроны в атомных листах графита полностью делокализованы на произвольных расстояниях и находятся на очень больших молекулярных орбиталях, которые покрывают весь графитовый лист, и поэтому некоторые электроны могут свободно перемещаться и, следовательно, проводить электричество в плоскости листа, как если бы они находились в металле.

Смотрите также

• Химический портал

• Цис-эффект
• Взаимодействие конфигурации
• Связанный кластер
• Пограничная теория молекулярных орбиталей
• Теория поля лигандов (теория МО для комплексов переходных металлов)
• Теория возмущений Мёллера–Плессе.
• Компьютерные программы квантовой химии
• Полуэмпирические методы квантовой химии
• Теория валентных связей

Ссылки

1. Daintith, J. (2004). Оксфордский словарь химии . Нью-Йорк: Oxford University Press. ISBN 978-0-19-860918-6.
2. Ликер, Марк, Дж. (2004). McGraw-Hill Concise Encyclopedia of Chemistry . Нью-Йорк: McGraw-Hill. ISBN 978-0-07-143953-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
3. Мисслер, Гэри Л.; Фишер, Пол Дж.; Тарр, Дональд А. (2013-04-08). Неорганическая химия. Pearson Education. ISBN 978-0-321-91779-9.
4. Коулсон, Чарльз, А. (1952). Валенсия . Оксфорд в Clarendon Press.{{cite book}}: CS1 maint: multiple names: authors list (link)
5. Малликен, Роберт С. (1972) [1966]. «Спектроскопия, молекулярные орбитали и химическая связь» (PDF) (пресс-релиз). Нобелевские лекции по химии 1963–1970. Амстердам: Elsevier Publishing Company.
6. Хюккель, Эрих (1934). «Теория свободных радикалов органической химии». Trans. Faraday Soc . 30 : 40–52. doi :10.1039/TF9343000040.
7. Lennard-Jones, JE (1929). «Электронная структура некоторых двухатомных молекул». Trans. Faraday Soc . 25 : 668–686. Bibcode :1929FaTr...25..668L. doi :10.1039/TF9292500668.
8. Коулсон, К. А. Валенс (2-е изд., Oxford University Press, 1961), стр. 103
9. Полинг, Лайнус (1931). «Природа химической связи. II. Одноэлектронная связь и трехэлектронная связь». J. Am. Chem. Soc . 53 (9): 3225–3237. doi :10.1021/ja01360a004.
10. Холл, Джордж Г. (1991). «Статья Леннарда-Джонса 1929 года и основы теории молекулярных орбиталей». Advances in Quantum Chemistry . 22 : 1–6. Bibcode : 1991AdQC...22....1H. doi : 10.1016/S0065-3276(08)60361-5. ISBN 978-0-12-034822-0. ISSN  0065-3276.
11. Э. Хюкель, Zeitschrift für Physik , 70 , 204 (1931); 72 , 310 (1931); 76 , 628 (1932); 83 , 632 (1933).
12. Теория Хюккеля для химиков-органиков , CA Coulson , B. O'Leary и RB Mallion, Academic Press, 1978.
13. Коулсон, К. А. (1938), «Самосогласованное поле для молекулярного водорода», Математические труды Кембриджского философского общества , 34 (2): 204–212, Bibcode : 1938PCPS...34..204C, doi : 10.1017/S0305004100020089, S2CID  95772081
14. Холл, ГГ (7 августа 1950 г.). «Теория молекулярных орбиталей химической валентности. VI. Свойства эквивалентных орбиталей». Proc. R. Soc. A. 202 ( 1070): 336–344. Bibcode : 1950RSPSA.202..336H. doi : 10.1098/rspa.1950.0104. S2CID  123260646.
15. Jensen, Frank (1999). Введение в вычислительную химию . John Wiley and Sons. ISBN 978-0-471-98425-2.
16. Мисслер и Тарр (2013), Неорганическая химия , 5-е изд., 117-165, 475-534.
17. Мисслер, Гэри Л.; Фишер, Пол Дж.; Тарр, Дональд А. (2013-04-08). Неорганическая химия. Pearson Education. ISBN 978-0-321-91779-9.
18. Малликен, RS (октябрь 1955 г.). «Анализ электронной популяции на молекулярных волновых функциях LCAO–MO. I». Журнал химической физики . 23 (10): 1833–1840. Bibcode : 1955JChPh..23.1833M. doi : 10.1063/1.1740588. ISSN  0021-9606.
19. Гриффит, Дж. С. и Л. Е. Орджел. «Теория поля лигандов». Q. Rev. Chem. Soc. 1957, 11, 381-383

Внешние ссылки

• Теория молекулярных орбиталей - Университет Пердью
• Теория молекулярных орбиталей - Sparknotes
• Теория молекулярных орбиталей - Химический сайт Марка Бишопа
• Введение в теорию МО — Королева Мэри, Лондонский университет
• Теория молекулярных орбиталей - таблица связанных терминов
• Введение в теорию молекулярных групп - Оксфордский университет