

В тригонометрии и геометрии триангуляция — это процесс определения местоположения точки путем построения треугольников к этой точке из известных точек.
В частности, в геодезии триангуляция подразумевает только измерение углов в известных точках, а не измерение расстояний до точки напрямую, как при трилатерации ; использование как угловых, так и расстоянийных измерений называется триангуляцией.
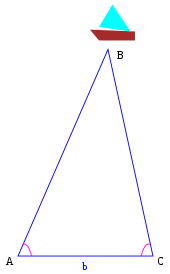
Компьютерное стереозрение и оптические 3D-измерительные системы используют этот принцип для определения пространственных размеров и геометрии объекта. [2] В основном конфигурация состоит из двух датчиков, наблюдающих за объектом. Один из датчиков, как правило, представляет собой цифровое устройство-камеру, а другой может быть также камерой или световым проектором. Центры проекций датчиков и рассматриваемая точка на поверхности объекта определяют (пространственный) треугольник. Внутри этого треугольника расстояние между датчиками является основанием b и должно быть известно. Определяя углы между проекционными лучами датчиков и основанием, точка пересечения и, таким образом, трехмерная координата вычисляются из треугольных соотношений.

Сегодня триангуляция используется для многих целей, включая геодезию , навигацию , метрологию , астрометрию , бинокулярное зрение , ракетное моделирование , а в военном деле — для определения направления стрельбы, траектории и распределения огневой мощи оружия .
Использование треугольников для оценки расстояний восходит к древности. В VI веке до нашей эры, примерно за 250 лет до основания династии Птолемеев , греческий философ Фалес упоминается как использовавший подобные треугольники для оценки высоты пирамид Древнего Египта . Он измерил длину тени пирамид и своей собственной в тот же момент и сравнил соотношения со своей высотой ( теорема отсекателя ). [3] Фалес также оценивал расстояния до кораблей в море, видимых с вершины скалы, измеряя горизонтальное расстояние, пройденное линией визирования для известного падения, и масштабируя до высоты всей скалы. [4] Такие методы были знакомы древним египтянам. Задача 57 папируса Райнда , на тысячу лет раньше, определяет сект или секед как отношение длины к подъему склона , т . е. обратную величину градиентов, измеряемых сегодня. Наклоны и углы измерялись с помощью визирной рейки, которую греки называли диоптрой , предшественником арабской алидады . Известен подробный современный сборник конструкций для определения длин на расстоянии с помощью этого инструмента, Диоптра Герона Александрийского ( ок. 10–70 гг. н. э.), которая сохранилась в арабском переводе; но эти знания были утеряны в Европе, пока в 1615 году Снеллиус , после работы Эратосфена , не переработал технику для попытки измерить окружность Земли. В Китае Пэй Сю (224–271) определил «измерение прямых и острых углов» как пятый из своих шести принципов для точного картографирования, необходимых для точного установления расстояний, [5] в то время как Лю Хуэй ( ок. 263 г.) дает версию расчета выше для измерения перпендикулярных расстояний до недоступных мест. [6] [7]
{{citation}}: CS1 maint: местоположение ( ссылка )