В математике , особенно в динамических системах , бифуркационная диаграмма показывает значения, достигнутые или достигнутые асимптотически (неподвижные точки, периодические орбиты или хаотические аттракторы ) системы как функцию параметра бифуркации в системе. [ требуется ссылка ] Обычно устойчивые значения представляются сплошной линией, а неустойчивые — пунктирной линией, хотя часто неустойчивые точки опускаются. Бифуркационные диаграммы позволяют визуализировать теорию бифуркации . В контексте динамических систем с дискретным временем диаграмма также называется орбитальной диаграммой .


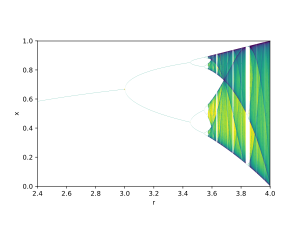
Примером может служить бифуркационная диаграмма логистической карты :
Параметр бифуркации r показан на горизонтальной оси графика, а вертикальная ось показывает набор значений логистической функции, достигаемых асимптотически почти из всех начальных условий.
Бифуркационная диаграмма показывает разветвление периодов устойчивых орбит от 1 к 2 к 4 к 8 и т.д. Каждая из этих точек бифуркации является бифуркацией удвоения периода . Отношение длин последовательных интервалов между значениями r, для которых происходит бифуркация, сходится к первой постоянной Фейгенбаума .
На диаграмме также показаны удвоения периодов от 3 до 6, до 12 и т. д., от 5 до 10, до 20 и т. д. и т. д.

В динамической системе, такой как которая структурно устойчива при , если построить диаграмму бифуркации, рассматривая как параметр бифуркации, но для разных значений , то это будет симметричная бифуркация вил. Когда , мы говорим, что имеем вилы с нарушенной симметрией. Это показано на анимации справа.
Рассмотрим систему дифференциальных уравнений , описывающую некоторую физическую величину, которая для конкретности может представлять один из трех примеров: 1. положение и скорость незатухающего и свободного от трения маятника, 2. мембранный потенциал нейрона с течением времени и 3. средняя концентрация вируса в кровотоке пациента. Дифференциальные уравнения для этих примеров включают *параметры*, которые могут влиять на вывод уравнений. Изменение массы и длины маятника повлияет на частоту его колебаний, изменение величины введенного в нейрон тока может перевести мембранный потенциал из состояния покоя в пиковое состояние, а долгосрочная вирусная нагрузка в кровотоке может уменьшиться при тщательно рассчитанном времени лечения.
В общем случае исследователи могут стремиться количественно оценить, как изменяется долгосрочное (асимптотическое) поведение системы дифференциальных уравнений при изменении параметра. В разделе математики динамических систем бифуркационная диаграмма количественно оценивает эти изменения, показывая, как неподвижные точки, периодические орбиты или хаотические аттракторы системы изменяются в зависимости от параметра бифуркации . Бифуркационные диаграммы используются для визуализации этих изменений.