Динамическое рассеяние света

Метод определения распределения частиц по размерам

Гипотетическое динамическое рассеяние света двумя образцами: более крупные частицы сверху и более мелкие частицы снизу

Динамическое рассеяние света ( DLS ) — это метод в физике , который может быть использован для определения профиля распределения размеров мелких частиц в суспензии или полимеров в растворе . ^[1] В рамках DLS временные флуктуации обычно анализируются с использованием функции автокорреляции интенсивности или фотонов (также известной как фотонная корреляционная спектроскопия — PCS или квазиупругое рассеяние света — QELS ). При анализе во временной области автокорреляционная функция (ACF) обычно затухает, начиная с нулевого времени задержки, а более быстрая динамика из-за более мелких частиц приводит к более быстрой декорреляции следа рассеянной интенсивности. Было показано, что ACF интенсивности является преобразованием Фурье спектра мощности , и поэтому измерения DLS могут быть одинаково хорошо выполнены в спектральной области. ^{[2] [3]} DLS также может быть использована для исследования поведения сложных жидкостей, таких как концентрированные полимерные растворы.

Настраивать

Источник монохроматического света, обычно лазер, пропускается через поляризатор и попадает в образец. Рассеянный свет затем проходит через второй поляризатор, где он собирается фотоумножителем, и полученное изображение проецируется на экран. Это известно как спекл-шаблон (рисунок 1). ^[4]

Рисунок 1. Типичный рисунок пятен.

Все молекулы в растворе подвергаются воздействию света, и все молекулы преломляют свет во всех направлениях. Дифрагированный свет от всех молекул может интерферировать либо конструктивно (светлые области), либо деструктивно (темные области). Этот процесс повторяется через короткие промежутки времени, и полученный набор спекл-структур анализируется автокоррелятором, который сравнивает интенсивность света в каждой точке с течением времени. Поляризаторы могут быть установлены в двух геометрических конфигурациях. Одна из них — это вертикальная (VV) геометрия, где второй поляризатор пропускает свет, который находится в том же направлении, что и первичный поляризатор. В вертикальной/горизонтальной (VH) геометрии второй поляризатор пропускает свет, который не находится в том же направлении, что и падающий свет.

Описание

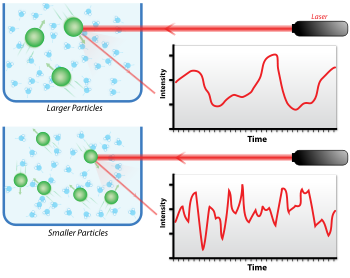
Когда свет попадает на мелкие частицы, он рассеивается во всех направлениях ( рэлеевское рассеяние ), пока частицы малы по сравнению с длиной волны (менее 250 нм ). Даже если источником света является лазер , и, следовательно, он монохроматичен и когерентен , интенсивность рассеяния колеблется со временем. Эта флуктуация обусловлена ​​тем, что мелкие частицы в суспензии совершают броуновское движение , и поэтому расстояние между рассеивателями в растворе постоянно меняется со временем. Затем этот рассеянный свет подвергается либо конструктивной, либо деструктивной интерференции со стороны окружающих частиц, и в этой флуктуации интенсивности содержится информация о временной шкале движения рассеивателей. Подготовка образца путем фильтрации или центрифугирования имеет решающее значение для удаления пыли и артефактов из раствора.

Динамическая информация о частицах выводится из автокорреляции следа интенсивности, записанного во время эксперимента. Кривая автокорреляции второго порядка генерируется из следа интенсивности следующим образом:

${\displaystyle g^{2}(q;\tau )={\frac {\langle I(t)I(t+\tau )\rangle }{\langle I(t)\rangle ^{2}}}}$

где g ² ( q ; τ ) — автокорреляционная функция при определенном волновом векторе q и времени задержки τ , а I — интенсивность. Угловые скобки обозначают оператор ожидаемого значения , который в некоторых текстах обозначается заглавной буквой E . ${\displaystyle \langle \cdot \rangle }$

При коротких задержках корреляция высока, поскольку у частиц нет возможности значительно изменить начальное состояние, в котором они находились. Таким образом, два сигнала по существу не изменяются при сравнении только через очень короткий промежуток времени. По мере увеличения задержек корреляция экспоненциально затухает, что означает, что по истечении длительного периода времени корреляция между рассеянной интенсивностью начального и конечного состояний отсутствует. Этот экспоненциальный затухание связан с движением частиц, в частности с коэффициентом диффузии. Для подгонки затухания (т. е. функции автокорреляции) используются численные методы, основанные на расчетах предполагаемых распределений. Если образец монодисперсный (однородный), то затухание представляет собой просто одну экспоненту. Уравнение Зигерта связывает функцию автокорреляции второго порядка с функцией автокорреляции первого порядка g ¹ ( q ; τ ) следующим образом:

${\displaystyle g^{2}(q;\tau )=1+\beta \left[g^{1}(q;\tau )\right]^{2}}$

где первый член суммы связан с базовым значением (≈1), а параметр β является поправочным коэффициентом, который зависит от геометрии и выравнивания лазерного луча в установке для рассеяния света. Он примерно равен обратной величине числа спеклов (см. Спекл-шаблон ), из которых собирается свет. Меньший фокус лазерного луча дает более грубый спекл-шаблон, меньшее число спеклов на детекторе и, следовательно, большую автокорреляцию второго порядка. Наиболее важным применением функции автокорреляции является ее использование для определения размера.

Многократное рассеяние

Динамическое рассеяние света дает представление о динамических свойствах мягких материалов путем измерения единичных событий рассеяния, что означает, что каждый обнаруженный фотон был рассеян образцом ровно один раз. В принципе, измерения DLS можно выполнять с детектором, расположенным под любым углом. Выбор наилучшего угла зависит от свойств образца, таких как мутность и размер частиц. ^[5] Детектирование обратного рассеяния (например, 173° или 175°) особенно интересно для мутных и высококонцентрированных образцов, которые содержат крупные частицы. Детектирование бокового рассеяния (90°) рекомендуется для слабо рассеивающих образцов, включая мелкие частицы и прозрачные образцы. Наконец, детектирование прямого рассеяния (например, 13° или 15°) подходит для обнаружения образцов, содержащих мелкие частицы с несколькими крупными частицами. Некоторые приборы DLS на рынке также позволяют автоматически выбирать угол на основе непрерывного измерения пропускания.

На нижнем конце диапазона мутности метод спектроскопии рассеяния с усилением в полости ^[6] использует интегрирующую полость для удлинения траекторий фотонов через квазинерассеивающие образцы. В отличие от обычных инструментов DLS, этот метод не зависит от угла, поскольку он зондирует образцы изотропно со всех направлений.

Несмотря на то, что измерение DLS с использованием одноуглового обнаружения было наиболее распространенным методом, его применение во многих системах научного и промышленного значения было ограничено из-за часто встречающегося многократного рассеяния, когда фотоны рассеиваются образцом несколько раз, прежде чем будут обнаружены. Точная интерпретация становится чрезвычайно сложной для систем с существенным вкладом многократного рассеяния. Особенно для более крупных частиц и частиц с высоким контрастом показателя преломления, это ограничивает метод очень низкими концентрациями частиц, и поэтому большое количество систем исключается из исследований с динамическим рассеянием света. Однако, как показал Шетцель ^[7], можно подавить многократное рассеяние в экспериментах по динамическому рассеянию света с помощью подхода кросс-корреляции. Общая идея заключается в том, чтобы изолировать однократно рассеянный свет и подавить нежелательные вклады многократного рассеяния в эксперименте по динамическому рассеянию света. Были разработаны и применены различные реализации кросс-корреляционного рассеяния света. В настоящее время наиболее широко используемой схемой является так называемый метод 3D-динамического рассеяния света. ^{[8] [9]} Этот же метод можно использовать для коррекции данных статического рассеяния света с учетом вклада многократного рассеяния. ^[10] В качестве альтернативы, в пределе сильного многократного рассеяния, можно применить вариант динамического рассеяния света, называемый спектроскопией диффузных волн .

Анализ данных

Введение

После того, как данные автокорреляции получены, можно использовать различные математические подходы для получения «информации» из них. Анализ рассеяния облегчается, когда частицы не взаимодействуют посредством столкновений или электростатических сил между ионами. Столкновения частиц могут быть подавлены путем разбавления, а эффекты заряда уменьшаются путем использования солей для разрушения двойного электрического слоя .

Самый простой подход — рассматривать автокорреляционную функцию первого порядка как одиночный экспоненциальный спад. Это подходит для монодисперсной популяции.

${\displaystyle \ g^{1}(q;\tau )=\exp(-\Gamma \tau )\,}$

где Γ — скорость распада. Коэффициент трансляционной диффузии D _t может быть получен для одного угла или для диапазона углов в зависимости от волнового вектора q .

${\displaystyle \ \Gamma =q^{2}D_{t}\,}$

с

${\displaystyle \ q={\frac {4\pi n_{0}}{\lambda }}\sin \left({\frac {\theta }{2}}\right)}$

где λ — длина волны падающего лазера, n ₀ — показатель преломления растворителя , а θ — угол, под которым детектор расположен по отношению к ячейке образца.

Показатель преломления растворителя играет решающую роль в рассеянии света и важен для расчета радиуса Стокса из уравнения Стокса-Эйнштейна . ^{[11] [12] [13]} Поэтому предыдущие данные показателя преломления рассеивающей среды следует оценивать с помощью специальных приборов, известных как рефрактометры . В качестве альтернативы приборы DLS, содержащие модуль измерения показателя преломления, позволяют получить хорошую оценку этого важного параметра в пределах ±0,5%, что является точностью, определенной ISO 22412:2017 ^{[14] [15] для значений показателя преломления, необходимых для DLS. Помимо показателя преломления среды, показатель преломления частиц необходим только при анализе более крупных размеров частиц (обычно более 100 нм), и необходимы объемно- или численно-взвешенные распределения размеров. В этих случаях для применения} рассеяния Ми требуются предварительные знания показателя преломления и поглощения материала . ^{[16] [17]}

В зависимости от анизотропии и полидисперсности системы, полученный график (Γ/ q ² ) против q ² может показывать или не показывать угловую зависимость. Маленькие сферические частицы не будут показывать угловой зависимости, следовательно, анизотропии. График (Γ/ q ² ) против q ² приведет к горизонтальной линии. Частицы с формой, отличной от сферы, будут демонстрировать анизотропию и, следовательно, угловую зависимость при построении графика (Γ/ q ² ) против q ² . ^[18] Пересечение в любом случае будет D _t . Таким образом, существует оптимальный угол обнаружения θ для каждого размера частицы. Высококачественный анализ всегда должен выполняться при нескольких углах рассеяния (многоугловой DLS). Это становится еще более важным в полидисперсном образце с неизвестным распределением размеров частиц. При определенных углах интенсивность рассеяния некоторых частиц будет полностью подавлять слабый сигнал рассеяния других частиц, тем самым делая их невидимыми для анализа данных под этим углом. Инструменты DLS, которые работают только под фиксированным углом, могут давать хорошие результаты только для некоторых частиц. Таким образом, указанная точность инструмента DLS с одним углом обнаружения верна только для определенных частиц.

D _t часто используется для расчета гидродинамического радиуса сферы с помощью уравнения Стокса–Эйнштейна. Важно отметить, что размер, определенный динамическим рассеянием света, является размером сферы, которая движется таким же образом, как рассеиватель. Так, например, если рассеиватель представляет собой полимер со случайной катушкой, определенный размер не совпадает с радиусом инерции, определенным статическим рассеянием света . Также полезно отметить, что полученный размер будет включать любые другие молекулы или молекулы растворителя, которые движутся вместе с частицей. Так, например, коллоидное золото со слоем поверхностно-активного вещества будет казаться больше при динамическом рассеянии света (которое включает слой поверхностно-активного вещества), чем при просвечивающей электронной микроскопии (которая не «видит» слой из-за плохого контраста).

В большинстве случаев выборки полидисперсны. Таким образом, автокорреляционная функция представляет собой сумму экспоненциальных спадов, соответствующих каждому из видов в популяции.

${\displaystyle g^{1}(q;\tau )=\sum _{i=1}^{n}G_{i}(\Gamma _{i})\exp(-\Gamma _{i}\tau )=\int G(\Gamma )\exp(-\Gamma \tau )\,d\Gamma .}$

Возникает соблазн получить данные для g ¹ ( q ; τ ) и попытаться инвертировать вышесказанное, чтобы извлечь G (Γ) . Поскольку G (Γ) пропорционален относительному рассеянию от каждого вида, он содержит информацию о распределении размеров. Однако это известно как некорректно поставленная задача. Описанные ниже методы (и другие) были разработаны для извлечения как можно большего количества полезной информации из функции автокорреляции.

Метод кумуляции

Одним из наиболее распространенных методов является метод кумулянтов , ^{[19] [20]} , из которого в дополнение к сумме экспонент, приведенных выше, можно получить дополнительную информацию о дисперсии системы следующим образом:

${\displaystyle \ g^{1}(q;\tau )=\exp \left(-{\bar {\Gamma }}\left(\tau -{\frac {\mu _{2}}{2!}}\tau ^{2}+{\frac {\mu _{3}}{3!}}\tau ^{3}+\cdots \right)\right)}$

где Γ — средняя скорость распада, а μ ₂ / Γ ² — индекс полидисперсности второго порядка (или показатель дисперсии). Индекс полидисперсности третьего порядка также может быть выведен, но это необходимо только в том случае, если частицы системы являются высокополидисперсными. Коэффициент трансляционной диффузии D _z , усредненный по z , может быть выведен для одного угла или для диапазона углов в зависимости от волнового вектора q .

${\displaystyle \ {\bar {\Gamma }}=q^{2}D_{z}\,}$

Следует отметить, что кумулянтный метод действителен для малых τ и достаточно узких G ( Γ ) . ^[21] Следует редко использовать параметры за пределами μ ₃ , поскольку переобучение данных со многими параметрами в разложении в степенной ряд сделает все параметры, включая и μ ₂ , менее точными. ^[22] Кумулянтный метод гораздо меньше подвержен влиянию экспериментального шума, чем методы, представленные ниже. ${\displaystyle \scriptstyle {\bar {\Gamma }}}$

Функция распределения размеров

Распределение размеров частиц также можно получить с помощью функции автокорреляции. Однако полидисперсные образцы плохо разрешаются с помощью анализа кумулянтного соответствия. Таким образом, сочетание алгоритмов неотрицательных наименьших квадратов (NNLS) с методами регуляризации, такими как регуляризация Тихонова , может использоваться для разрешения многомодальных образцов. ^[16] Важной особенностью оптимизации NNLS является член регуляризации, используемый для определения конкретных решений и минимизации отклонения между данными измерений и соответствием. Не существует идеального члена регуляризации, который подходит для всех образцов. Форма этого члена может определить, будет ли решение представлять собой общее широкое распределение с небольшим числом пиков или будут подходить узкие и дискретные популяции. В качестве альтернативы расчет распределения размеров частиц выполняется с помощью алгоритма CONTIN.

Алгоритм КОНТИН

Альтернативный метод анализа функции автокорреляции может быть реализован с помощью обратного преобразования Лапласа, известного как CONTIN, разработанного Стивеном Провенчером. ^{[23] [24]} Анализ CONTIN идеально подходит для гетеродисперсных, полидисперсных и многомодальных систем, которые не могут быть разрешены с помощью кумулянтного метода. Разрешение для разделения двух различных популяций частиц составляет приблизительно пять или более раз, а разница в относительных интенсивностях между двумя различными популяциями должна быть меньше 1: ¹⁰⁻⁵ .

Метод максимальной энтропии

Метод максимальной энтропии — это метод анализа, который имеет большой потенциал развития. Этот метод также используется для количественной оценки данных скорости седиментации из аналитического ультрацентрифугирования . Метод максимальной энтропии включает несколько итерационных шагов для минимизации отклонения подобранных данных от экспериментальных данных и последующего уменьшения χ ² подобранных данных.

Рассеяние несферических частиц

Если рассматриваемая частица не сферическая, вращательное движение также должно быть рассмотрено, поскольку рассеяние света будет различным в зависимости от ориентации. Согласно Пекоре, вращательное броуновское движение будет влиять на рассеяние, когда частица удовлетворяет двум условиям: она должна быть как оптически, так и геометрически анизотропной. ^[25] Стержневидные молекулы удовлетворяют этим требованиям, поэтому коэффициент вращательной диффузии должен быть рассмотрен в дополнение к коэффициенту поступательной диффузии. В наиболее краткой форме уравнение выглядит как

${\displaystyle {\frac {A}{B}}={\frac {5}{4}}{\frac {4\mathrm {M} _{p}+2\mathrm {N} \mathrm {M} _{l}\mathrm {M} _{p}+\mathrm {M} _{l}}{\mathrm {M} _{p}-\mathrm {N} +\mathrm {M} _{l}}}}$

Где A / B — отношение двух релаксационных мод (поступательной и вращательной), Mp содержит информацию об оси _, перпендикулярной центральной оси частицы, а Ml содержит информацию об оси, параллельной центральной оси _.

В 2007 году Питер Р. Лэнг и его команда решили использовать динамическое рассеяние света для определения длины частиц и соотношения сторон коротких золотых наностержней. ^[26] Они выбрали этот метод, поскольку он не разрушает образец и имеет относительно простую настройку. Оба состояния релаксации наблюдались в геометрии VV, а коэффициенты диффузии обоих движений использовались для расчета соотношений сторон золотых наночастиц.

Приложения

DLS используется для характеристики размера различных частиц, включая белки, ^[27] полимеры, мицеллы, ^[28] белковые клетки и вирусоподобные частицы, ^{[29] [30]} везикулы, ^[31] углеводы, наночастицы, биологические клетки, ^[32] и гели. ^[33] Если система не является дисперсной по размеру, можно определить средний эффективный диаметр частиц. Это измерение зависит от размера ядра частицы, размера поверхностных структур, концентрации частиц и типа ионов в среде.

Поскольку DLS по сути измеряет флуктуации интенсивности рассеянного света из-за рассеивающихся частиц, можно определить коэффициент диффузии частиц. Программное обеспечение DLS коммерческих приборов обычно отображает популяцию частиц при разных диаметрах. Если система монодисперсная, должна быть только одна популяция, тогда как полидисперсная система будет отображать несколько популяций частиц. Если в образце присутствует более одной популяции размера, то либо анализ CONTIN следует применять для приборов фотонной корреляционной спектроскопии, либо метод спектра мощности следует применять для приборов доплеровского сдвига.

Исследования стабильности можно удобно проводить с помощью DLS. Периодические измерения DLS образца могут показать, агрегируют ли частицы со временем, наблюдая, увеличивается ли гидродинамический радиус частицы. Если частицы агрегируют, будет большее количество частиц с большим радиусом. В некоторых машинах DLS стабильность в зависимости от температуры можно анализировать, контролируя температуру in situ .

Смотрите также

• Дифференциальная динамическая микроскопия
• Дифференциальное статическое рассеяние света (DSLS)
• Спектроскопия диффузионных волн
• Коэффициент диффузии
• Флуоресцентная корреляционная спектроскопия
• Микроскопия интерферометрического рассеяния
• Рассеивание света
• Рассеивание света под разными углами
• Анализ траектории наночастиц
• Белково-белковые взаимодействия
• Сканирование ионной окклюзионной зондировки
• Статическое рассеяние света
• Радиус Стокса

Ссылки

1. Берн, Б. Дж.; Пекора, Р. Динамическое рассеяние света. Courier Dover Publications (2000) ISBN  0-486-41155-9
2. Чу, Б. (1 января 1970 г.). «Рассеяние лазерного света». Annual Review of Physical Chemistry . 21 (1): 145–174. Bibcode : 1970ARPC...21..145C. doi : 10.1146/annurev.pc.21.100170.001045.
3. Pecora., R. (1964). «Доплеровские сдвиги в рассеянии света чистыми жидкостями и полимерными растворами». Журнал химической физики . 40 (6): 1604. Bibcode : 1964JChPh..40.1604P. doi : 10.1063/1.1725368.
4. Гудман, Дж. (1976). «Некоторые фундаментальные свойства спекла». J. Opt. Soc. Am . 66 (11): 1145–1150. Bibcode : 1976JOSA...66.1145G. doi : 10.1364/josa.66.001145.
5. "Multiple detection angles in dynamic light scattering analysis :: Anton Paar Wiki". Антон Паар (на немецком языке) . Получено 31 мая 2022 г.
6. Грациани, Гийом; Кинг, Джон Т.; Амблар, Франсуа (30 августа 2022 г.). «Спектроскопия рассеяния с усилением резонатором выявляет динамику белков и наночастиц в квазипрозрачных и миниатюрных образцах». ACS Nano . 16 (10): 16796–16805. arXiv : 2111.09616 . doi :10.1021/acsnano.2c06471. ISSN  1936-0851. PMID  36039927. S2CID  244345602.
7. Schaetzel, K. (1991). "Подавление многократного рассеяния методами кросс-корреляции фотонов" (PDF) . J. Mod. Opt . 38 : 1849. Bibcode :1990JPCM....2..393S. doi :10.1088/0953-8984/2/S/062. S2CID  250745836 . Получено 7 апреля 2014 г. .
8. Urban, C.; Schurtenberger, P. (1998). «Характеристика мутных коллоидных суспензий с использованием методов рассеяния света в сочетании с методами кросс-корреляции». J. Colloid Interface Sci . 207 (1): 150–158. Bibcode :1998JCIS..207..150U. doi :10.1006/jcis.1998.5769. PMID  9778402.
9. Блок, И.; Шеффолд, Ф. (2010). «Модулированное 3D кросс-корреляционное рассеяние света: улучшение характеристики мутных образцов». Обзор научных инструментов . 81 (12): 123107–123107–7. arXiv : 1008.0615 . Bibcode :2010RScI...81l3107B. doi :10.1063/1.3518961. PMID  21198014. S2CID  9240166.
10. Pusey, PN (1999). «Подавление многократного рассеяния методами кросс-корреляции фотонов». Current Opinion in Colloid & Interface Science . 4 (3): 177–185. doi :10.1016/S1359-0294(99)00036-9.
11. Strutt, JW (1 июня 1871 г.). «LVIII. О рассеянии света малыми частицами». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 41 (275): 447–454. doi :10.1080/14786447108640507. ISSN  1941-5982.
12. Strutt, JW (1 апреля 1871 г.). «XXXVI. О свете с неба, его поляризации и цвете». The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 41 (273): 274–279. doi :10.1080/14786447108640479. ISSN  1941-5982.
13. Штетефельд, Йорг; Маккенна, Шон А.; Патель, Трушар Р. (1 декабря 2016 г.). «Динамическое рассеяние света: практическое руководство и применение в биомедицинских науках». Biophysical Reviews . 8 (4): 409–427. doi :10.1007/s12551-016-0218-6. ISSN  1867-2469. PMC 5425802 . PMID  28510011. 
14. "ISO 22412:2017. Анализ размера частиц — Динамическое рассеяние света (DLS)". ISO . Получено 31 мая 2022 г. .
15. Тарек, Сайед Мохаммед; Бутчуен, Армель; Рой, Шувашиш; Циммерман, Делл; Джур, Гитапун; Бати, Джеджаль Редди; Палчоудхури, Субантика (август 2021 г.). «Подход динамического рассеяния света для обнаружения наноматериалов в реке Теннесси». Water Resources Research . 57 (8). Bibcode : 2021WRR....5728687T. doi : 10.1029/2020WR028687. ISSN  0043-1397. S2CID  238831573.
16. "White Paper: Understanding the Concept of Dynamic Light Scattering :: Anton-Paar.com". Антон Паар . Получено 31 мая 2022 г.
17. Альфано, Бригида; Барретта, Луиджи; Дель Джудиче, Антонио; Де Вито, Саверио; Ди Франсия, Джироламо; Эспозито, Елена; Формизано, Фабрицио; Массера, Этторе; Миглиетта, Мария Люсия; Поличетти, Тициана (29 ноября 2020 г.). «Обзор недорогих датчиков твердых частиц с точки зрения разработчиков». Датчики . 20 (23): 6819. Бибкод : 2020Senso..20.6819A. дои : 10.3390/s20236819 . ISSN  1424-8220. ПМЦ 7730878 . ПМИД  33260320. 
18. Гои, Жан-Франсуа; Варшни, Сунил К.; Жером, Роберт (2001). «Водорастворимые комплексы, образованные сополимерами поли(2-винилпиридиния)-блок-поли(этиленоксида) и поли(метакрилата натрия)-блок-поли(этиленоксида)». Макромолекулы . 34 (10): 3361. Bibcode : 2001MaMol..34.3361G. doi : 10.1021/ma0020483.
19. Коппель, Деннис Э. (1972). «Анализ полидисперсности макромолекул в спектроскопии корреляции интенсивности: метод кумулянтов». Журнал химической физики . 57 (11): 4814–4820. Bibcode : 1972JChPh..57.4814K. doi : 10.1063/1.1678153.
20. Фрискен, Барбара Дж. (2001). «Пересмотр метода кумулянтов для анализа данных динамического рассеяния света» (PDF) . Прикладная оптика . 40 (24): 4087–91. Bibcode :2001ApOpt..40.4087F. doi :10.1364/AO.40.004087. PMID  18360445.
21. Хассан, Па; Кулшрешта, Ск (август 2006 г.). «Модификация кумулянтного анализа полидисперсности в данных квазиупругого рассеяния света». Журнал коллоидной и интерфейсной науки . 300 (2): 744–8. Bibcode : 2006JCIS..300..744H. doi : 10.1016/j.jcis.2006.04.013. ISSN  0021-9797. PMID  16790246.
22. Чу, Б. (1992). Рассеивание лазерного света: основные принципы и практика . Academic Press. ISBN 978-0-12-174551-6.
23. Provencher, S (1982). "CONTIN: Программа ограниченной регуляризации общего назначения для обращения зашумленных линейных алгебраических и интегральных уравнений" (PDF) . Computer Physics Communications . 27 (3): 229–242. Bibcode :1982CoPhC..27..229P. doi :10.1016/0010-4655(82)90174-6.
24. Provencher, SW (1982). "Метод ограниченной регуляризации для инвертирования данных, представленных линейными алгебраическими или интегральными уравнениями" (PDF) . Comput. Phys. Commun . 27 (3): 213–227. Bibcode :1982CoPhC..27..213P. doi :10.1016/0010-4655(82)90173-4.
25. Арагон, SR; Пекора, Р. (1976). "Теория динамического рассеяния света полидисперсными системами". Журнал химической физики . 64 (6): 2395. Bibcode : 1976JChPh..64.2395A. doi : 10.1063/1.432528.
26. Родригес-Фернандес, Х.; Перес-Хусте, Х.; Лиз-Марзан, Л. М.; Ланг, П. Р. (2007). «Динамическое рассеяние света короткими золотыми стержнями с низким соотношением сторон» (PDF) . Журнал физической химии . 111 (13): 5020–5025. doi :10.1021/jp067049x.
27. Долинска, Моника Б.; Янг, Кеннет Л.; Кассуф, Клаудия; Димитриадис, Эмилиос К.; Вингфилд, Пол Т.; Сергеев, Юрий В. (3 января 2020 г.). "Protein Stability and Functional Characterization of Intra-Melanosomal Domain of Human Recombinant Tyrosinase-Related Protein 1". International Journal of Molecular Sciences . 21 (1): 331. doi : 10.3390/ijms21010331 . ISSN  1422-0067. PMC 6981619 . PMID  31947795. 
28. Bhut, Parth Rajeshkumar; Pal, Nilandjan; Mandal, Ajay (3 декабря 2019 г.). «Характеристика гидрофобно модифицированного полиакриламида в смешанных системах полимер-поверхностно-активное вещество Gemini для повышения нефтеотдачи». ACS Omega . 4 (23): 20164–20177. doi :10.1021/acsomega.9b02279. ISSN  2470-1343. PMC 6893946 . PMID  31815217. 
29. Waghwani HK, Douglas, T (март 2021 г.). «Цитохром C с пероксидазоподобной активностью, инкапсулированный внутри небольшой наноклетки белка DPS». Journal of Materials Chemistry B. 9 ( 14): 3168–3179. doi : 10.1039/d1tb00234a . PMID  33885621.
30. Waghwani HK, Uchida M, Douglas, T (апрель 2020 г.). «Вирусоподобные частицы (VLP) как платформа для иерархической компартментализации». Biomacromolecules . 21 (6): 2060–2072. doi : 10.1021/acs.biomac.0c00030 . PMID  32319761.
31. Velu, Sabareesh KP; Yan, Minhao; Tseng, Kuo-Pi; Wong, Ken-Tsung; Bassani, Dario M.; Terech, Pierre (6 февраля 2013 г.). «Спонтанное образование искусственных везикул в органических средах посредством водородных связей». Macromolecules . 46 (4): 1591–1598. Bibcode :2013MaMol..46.1591V. doi :10.1021/ma302595g.
32. Йена, Сидхартха С.; Джоши, Хирен М.; Сабариш, КПВ; Тата, БВР; Рао, ТС (2006). «Динамика Deinococcus radiodurans в условиях контролируемого роста». Биофизический журнал . 91 (7): 2699–2707. Бибкод : 2006BpJ....91.2699J. doi : 10.1529/biophysj.106.086520. ПМЦ 1562370 . ПМИД  16829564. 
33. Sabareesh, KPV; Jena, Sidhartha S.; Tata, BVR (5 мая 2006 г.). «Исследования динамического рассеяния света на фотополимеризованных и химически сшитых полиакриламидных гидрогелях». Труды конференции AIP . 832 (1): 307–310. Bibcode : 2006AIPC..832..307S. doi : 10.1063/1.2204513. ISSN  0094-243X.

Внешние ссылки

• DLS для определения радиуса мелких шариков в броуновском движении в растворе
• Определение размера частиц с помощью DLS
• Динамическое рассеяние света для характеристики размера частиц белков, полимеров и коллоидных дисперсий
• Понимание динамического рассеяния света, Wyatt Technology