Релятивистский эффект Доплера

Scientific phenomenon

Рисунок 1. Источник световых волн, движущийся вправо относительно наблюдателей со скоростью 0,7 с . Частота выше для наблюдателей справа и ниже для наблюдателей слева.

Релятивистский эффект Доплера — это изменение частоты , длины волны и амплитуды ^[1] света, вызванное относительным движением источника и наблюдателя (как в классическом эффекте Доплера ), при учёте эффектов, описываемых специальной теорией относительности .

Релятивистский эффект Доплера отличается от нерелятивистского эффекта Доплера , поскольку уравнения включают эффект замедления времени специальной теории относительности и не включают среду распространения в качестве точки отсчета. Они описывают общую разницу в наблюдаемых частотах и ​​обладают требуемой симметрией Лоренца .

Астрономам известны три источника красного смещения / синего смещения : доплеровские смещения; гравитационные красные смещения (из-за выхода света из гравитационного поля); и космологическое расширение (когда само пространство растягивается). В этой статье рассматриваются только доплеровские смещения.

Резюме основных результатов

В следующей таблице предполагается, что приемник и источник удаляются друг от друга, причем относительная скорость и скорость света, а . ${\displaystyle \beta =v/c>0}$ ${\displaystyle r}$ ${\displaystyle s}$ ${\displaystyle v}$ ${\displaystyle c}$ ${\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}$

Вывод

Релятивистский продольный эффект Доплера

Релятивистский доплеровский сдвиг для продольного случая, когда источник и приемник движутся прямо друг к другу или друг от друга, часто выводится так, как если бы это было классическое явление, но модифицированное добавлением члена замедления времени . ^{[2] [3]} Этот подход используется в учебниках физики или механики для первого года обучения, таких как учебники Фейнмана ^[4] или Морена. ^[5]

Следуя этому подходу к выводу релятивистского продольного эффекта Доплера, предположим, что приемник и источник движутся друг от друга с относительной скоростью , измеряемой наблюдателем на приемнике или источнике (принятое здесь соглашение о знаках таково, что знак отрицательный , если приемник и источник движутся навстречу друг другу). ${\displaystyle v\,}$ ${\displaystyle v\,}$

Рассмотрим задачу в системе отсчета источника.

Предположим, что один волновой фронт достигает приемника. Следующий волновой фронт тогда находится на расстоянии от приемника (где — длина волны , — частота волн, излучаемых источником, — скорость света ). ${\displaystyle \lambda _{s}=c/f_{s}\,}$ ${\displaystyle \lambda _{s}\,}$ ${\displaystyle f_{s}\,}$ ${\displaystyle c\,}$

Волновой фронт движется со скоростью , но в то же время приемник удаляется со скоростью в течение времени , которое является периодом световых волн, падающих на приемник, как это наблюдается в системе отсчета источника. Итак, где - скорость приемника в терминах скорости света. Соответствующая частота , с которой волновые фронты падают на приемник в системе отсчета источника, равна: ${\displaystyle c\,}$ ${\displaystyle v}$ ${\displaystyle t_{r,s}}$ $${\displaystyle \lambda _{s}+vt_{r,s}=ct_{r,s}\Longleftrightarrow \lambda _{s}=ct_{r,s}(1-v/c)\Longleftrightarrow t_{r,s}={\frac {1}{f_{s}(1-\beta )}},}$$ ${\displaystyle \beta =v/c\,}$ ${\displaystyle f_{r,s}}$ $${\displaystyle f_{r,s}=1/t_{r,s}=f_{s}(1-\beta ).}$$

До сих пор уравнения были идентичны уравнениям классического эффекта Доплера с неподвижным источником и движущимся приемником.

Однако из-за релятивистских эффектов часы на приемнике растянуты по времени относительно часов на источнике: , где - фактор Лоренца . Чтобы узнать, какое время растянуто, вспомним, что это время в системе отсчета, в которой источник находится в состоянии покоя. Приемник будет измерять полученную частоту, чтобы быть ${\displaystyle t_{r}=t_{r,s}/\gamma }$ ${\textstyle \gamma =1/{\sqrt {1-\beta ^{2}}}}$ ${\displaystyle t_{r,s}}$

Уравнение 1:    ${\displaystyle f_{r}=f_{r,s}\gamma }$ ${\displaystyle ={\frac {1-\beta }{\sqrt {1-\beta ^{2}}}}f_{s}}$ ${\displaystyle ={\sqrt {\frac {1-\beta }{1+\beta }}}\,f_{s}.}$

Соотношение

${\displaystyle {\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}}}$

называется фактором Доплера источника относительно приемника. (Эта терминология особенно распространена в области астрофизики : см. релятивистское излучение .)

Соответствующие длины волн связаны соотношением

Уравнение 2:    ${\displaystyle {\frac {\lambda _{r}}{\lambda _{s}}}={\frac {f_{s}}{f_{r}}}={\sqrt {\frac {1+\beta }{1-\beta }}},}$

Идентичные выражения для релятивистского доплеровского сдвига получаются при выполнении анализа в системе отсчета приемника с движущимся источником. Это соответствует ожиданиям принципа относительности , который диктует, что результат не может зависеть от того, какой объект считается покоящимся. Напротив, классический нерелятивистский эффект Доплера зависит от того, является ли источник или приемник неподвижным по отношению к среде. ^{[4] [5]}

Поперечный эффект Доплера

Предположим, что источник и приемник приближаются друг к другу в равномерном инерционном движении по траекториям, которые не сталкиваются. Поперечный эффект Доплера (TDE) может относиться к (a) номинальному синему смещению, предсказанному специальной теорией относительности , которое происходит, когда излучатель и приемник находятся в точках наибольшего сближения; или (b) номинальному красному смещению, предсказанному специальной теорией относительности, когда приемник видит излучатель находящимся в точке наибольшего сближения. ^[5] Поперечный эффект Доплера является одним из главных новых предсказаний специальной теории относительности.

Описывает ли научный отчет TDE как красное смещение или синее смещение, зависит от особенностей экспериментальной установки, с которой он связан. Например, первоначальное описание TDE Эйнштейном в 1907 году описывало экспериментатора, смотрящего на центр (ближайшую точку) пучка «каналовых лучей » (пучок положительных ионов, создаваемый определенными типами газоразрядных трубок). Согласно специальной теории относительности, испускаемая движущимися ионами частота будет уменьшена на фактор Лоренца, так что принимаемая частота будет уменьшена (смещена в красную область) на тот же фактор. ^{[стр. 1] [примечание 1]}

С другой стороны, Кюндиг (1963) описал эксперимент, в котором мёссбауэровский поглотитель вращался по быстрой круговой траектории вокруг центрального мёссбауэровского излучателя. ^{[стр. 3]} Как объясняется ниже, эта экспериментальная установка привела к измерению Кюндигом синего смещения.

Источник и приемник находятся в точках наибольшего сближения.

Рисунок 2. Источник и приемник находятся в точках наибольшего сближения. (а) Анализ в кадре приемника. (б) Анализ в кадре источника.

В этом сценарии точка наибольшего сближения не зависит от кадра и представляет собой момент, когда нет никаких изменений расстояния по сравнению со временем. Рисунок 2 демонстрирует, что простота анализа этого сценария зависит от кадра, в котором он анализируется. ^[5]

• Рис. 2а. Если проанализировать сценарий в кадре приемника, то окажется, что анализ сложнее, чем должен быть. Видимое положение небесного объекта смещено относительно его истинного положения (или геометрического положения) из-за движения объекта в течение времени, необходимого его свету, чтобы достичь наблюдателя. Источник будет растянут во времени относительно приемника, но красное смещение, подразумеваемое этим замедлением времени, будет компенсировано синим смещением из-за продольной составляющей относительного движения между приемником и видимым положением источника.
• Рис. 2б. Намного проще, если вместо этого мы проанализируем сценарий из кадра источника. Наблюдатель, находящийся у источника, знает из постановки задачи, что приемник находится в ближайшей к нему точке. Это означает, что приемник не имеет продольной составляющей движения, которая усложняет анализ. (т.е. dr/dt = 0, где r — расстояние между приемником и источником) Поскольку часы приемника растянуты во времени относительно источника, свет, который принимает приемник, смещен в синюю сторону на коэффициент гамма. Другими словами,

Ур. 3:    ${\displaystyle f_{r}=\gamma f_{s}}$

Приемниквидитисточник, находящийся в ближайшей точке

Рисунок 3. Поперечный доплеровский сдвиг для сценария, в котором приемник видит источник как находящийся в ближайшей к нему точке.

Этот сценарий эквивалентен приемнику, смотрящему под прямым углом к ​​траектории источника. Анализ этого сценария лучше всего проводить из кадра приемника. На рисунке 3 показано, что приемник освещается светом, когда источник был ближе всего к приемнику, даже если источник переместился. ^[5] Поскольку часы источника являются замедленными по времени, как измерено в кадре приемника, и поскольку нет продольной составляющей его движения, свет от источника, испускаемый из этой ближайшей точки, смещается в красную область с частотой

Ур. 4:    ${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}}$

В литературе большинство сообщений о поперечном доплеровском смещении анализируют эффект с точки зрения приемника, направленного под прямым углом к ​​траектории источника, таким образом, рассматривая источник как находящийся в ближайшей точке и наблюдая красное смещение.

Точка нулевого сдвига частоты

Рисунок 4. Нулевой сдвиг частоты происходит для импульса, который проходит кратчайшее расстояние от источника до приемника.

Учитывая, что в случае, когда инерциально движущиеся источник и приемник геометрически находятся на максимальном расстоянии друг от друга, приемник наблюдает смещение в синюю сторону, тогда как в случае, когда приемник видит источник в ближайшей точке, приемник наблюдает смещение в красную сторону, очевидно, должна существовать точка, в которой смещение в синюю сторону меняется на смещение в красную сторону. На рис. 2 сигнал распространяется перпендикулярно пути приемника и смещается в синюю сторону. На рис. 3 сигнал распространяется перпендикулярно пути источника и смещается в красную сторону.

Как видно на рис. 4, нулевой сдвиг частоты происходит для импульса, который проходит кратчайшее расстояние от источника до приемника. При просмотре в кадре, где источник и приемник имеют одинаковую скорость, этот импульс излучается перпендикулярно пути источника и принимается перпендикулярно пути приемника. Импульс излучается немного раньше точки наибольшего сближения и принимается немного позже. ^[6]

Один объект совершает круговое движение вокруг другого

Рисунок 5. Поперечный эффект Доплера для двух сценариев: (а) приемник движется по окружности вокруг источника; (б) источник движется по окружности вокруг приемника.

Рис. 5 иллюстрирует два варианта этого сценария. Оба варианта можно проанализировать с использованием простых аргументов замедления времени. ^[5] Рисунок 5a по сути эквивалентен сценарию, описанному на рисунке 2b, и приемник наблюдает свет от источника как смещенный в синюю сторону с коэффициентом . Рисунок 5b по сути эквивалентен сценарию, описанному на рисунке 3, и свет смещен в красную сторону. ${\displaystyle \gamma }$

Единственное кажущееся осложнение заключается в том, что вращающиеся по орбите объекты находятся в ускоренном движении. Ускоренная частица не имеет инерциальной системы отсчета, в которой она всегда находится в состоянии покоя. Однако всегда можно найти инерциальную систему отсчета, которая на мгновение сопутствует частице. Эта система отсчета, мгновенно сопутствующая система отсчета (MCRF) , позволяет применять специальную теорию относительности к анализу ускоренных частиц. Если инерциальный наблюдатель смотрит на ускоряющиеся часы, то при вычислении замедления времени важна только мгновенная скорость часов. ^[7]

Обратное, однако, неверно. Анализ сценариев, где оба объекта находятся в ускоренном движении, требует несколько более сложного анализа. Непонимание этого момента привело к путанице и недоразумениям.

Источник и приемник оба находятся в круговом движении вокруг общего центра.

Рисунок 6. Источник и приемник расположены на противоположных концах ротора, на равном расстоянии от центра.

Предположим, что источник и приемник расположены на противоположных концах вращающегося ротора, как показано на рис. 6. Кинематические аргументы (специальная теория относительности) и аргументы, основанные на том, что в псевдогравитационном поле ротора нет разницы в потенциале между источником и приемником (общая теория относительности), приводят к выводу, что между источником и приемником не должно быть доплеровского сдвига.

В 1961 году Чампени и Мун провели эксперимент с ротором Мёссбауэра, проверяя именно этот сценарий, и обнаружили, что процесс поглощения Мёссбауэра не зависит от вращения. ^{[стр. 4]} Они пришли к выводу, что их выводы подтверждают специальную теорию относительности.

Этот вывод вызвал некоторые споры. Некий настойчивый критик теории относительности ^{[ кто? ]} утверждал, что, хотя эксперимент согласуется с общей теорией относительности, он опровергает специальную теорию относительности, его точка зрения заключалась в том, что поскольку излучатель и поглотитель находились в равномерном относительном движении, специальная теория относительности требовала, чтобы наблюдался доплеровский сдвиг. Ошибочность аргумента этого критика заключалась, как показано в разделе Точка нулевого сдвига частоты, в том, что просто неверно, что доплеровский сдвиг всегда должен наблюдаться между двумя системами в равномерном относительном движении. ^[8] Кроме того, как показано в разделе Источник и приемник находятся в точках наибольшего сближения, сложность анализа релятивистского сценария часто зависит от выбора системы отсчета. Попытка проанализировать сценарий в системе отсчета приемника требует много утомительной алгебры. Гораздо проще, почти тривиально, установить отсутствие доплеровского сдвига между излучателем и поглотителем в лабораторной системе отсчета. ^[8]

Однако на самом деле эксперимент Чампени и Муна не сказал ничего ни за, ни против специальной теории относительности. Из-за симметрии установки оказывается, что практически любая мыслимая теория доплеровского сдвига между системами отсчета в равномерном инерциальном движении должна дать нулевой результат в этом эксперименте. ^[8]

Вместо того, чтобы быть равноудаленными от центра, предположим, что излучатель и поглотитель находятся на разных расстояниях от центра ротора. Для излучателя на радиусе и поглотителя на радиусе в любой точке ротора отношение частоты излучателя и частоты поглотителя определяется как ${\displaystyle R'}$ ${\displaystyle R}$ ${\displaystyle f',}$ ${\displaystyle f,}$

Уравнение 5:    ${\displaystyle {\frac {f'}{f}}=\left({\frac {c^{2}-R^{2}\omega ^{2}}{c^{2}-R'^{2}\omega ^{2}}}\right)^{1/2}}$

где - угловая скорость ротора. Источник и излучатель не обязательно должны быть на 180° друг от друга, но могут быть под любым углом относительно центра. ^{[стр. 5] [9]} ${\displaystyle \omega }$

Движение в произвольном направлении

Рисунок 7. Доплеровский сдвиг при движении источника под произвольным углом относительно линии между источником и приемником.

Анализ, использованный в разделе Релятивистский продольный эффект Доплера, может быть расширен простым способом для вычисления доплеровского сдвига для случая, когда инерционные движения источника и приемника происходят под любым заданным углом. ^{[3] [10]} На рис. 7 представлен сценарий из кадра приемника, при этом источник движется со скоростью под углом, измеренным в кадре приемника. Радиальная составляющая движения источника вдоль луча зрения равна ${\displaystyle v}$ ${\displaystyle \theta _{r}}$ ${\displaystyle v\cos {\theta _{r}}.}$

Уравнение ниже можно интерпретировать как классический доплеровский сдвиг для неподвижного и движущегося источника, измененный фактором Лоренца. ${\displaystyle \gamma :}$

Ур. 6:    ${\displaystyle f_{r}={\frac {f_{s}}{\gamma \left(1+\beta \cos \theta _{r}\right)}}.}$

В случае, когда , получается поперечный эффект Доплера: ${\displaystyle \theta _{r}=90^{\circ }}$

${\displaystyle f_{r}={\frac {f_{s}}{\gamma }}.\,}$

В своей статье 1905 года по специальной теории относительности ^{[стр. 2]} Эйнштейн получил несколько иное на вид уравнение для уравнения сдвига Доплера. После изменения названий переменных в уравнении Эйнштейна, чтобы они соответствовали тем, которые используются здесь, его уравнение читается как

Ур. 7:    ${\displaystyle f_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)f_{s}.}$

Различия возникают из-за того, что Эйнштейн оценивал угол относительно исходной системы отсчета, а не относительно приемной системы отсчета. не равно из- за эффекта релятивистской аберрации . Уравнение релятивистской аберрации имеет вид: ${\displaystyle \theta _{s}}$ ${\displaystyle \theta _{s}}$ ${\displaystyle \theta _{r}}$

Ур. 8:    ${\displaystyle \cos \theta _{r}={\frac {\cos \theta _{s}-\beta }{1-\beta \cos \theta _{s}}}\,}$

Подстановка уравнения релятивистской аберрации (Уравнение 8) в Уравнение 6 дает Уравнение 7 , демонстрирующее согласованность этих альтернативных уравнений для доплеровского сдвига. ^[10]

Подстановка в Уравнение 6 или в Уравнение 7 дает Уравнение 1 — выражение для релятивистского продольного доплеровского сдвига. ${\displaystyle \theta _{r}=0}$ ${\displaystyle \theta _{s}=0}$

Четырехвекторный подход к получению этих результатов можно найти в работе Ландау и Лифшица (2005). ^[11]

В электромагнитных волнах амплитуды электрического и магнитного полей E и B преобразуются аналогично частоте: ^[12]

${\displaystyle E_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)E_{s}}$

${\displaystyle B_{r}=\gamma \left(1-\beta \cos \theta _{s}\right)B_{s}.}$

Визуализация

Рисунок 8. Сравнение релятивистского эффекта Доплера (вверху) с нерелятивистским эффектом (внизу).

Рис. 8 помогает нам понять, в грубом качественном смысле, чем релятивистский эффект Доплера и релятивистская аберрация отличаются от нерелятивистского эффекта Доплера и нерелятивистской аберрации света . Предположим, что наблюдатель равномерно окружен во всех направлениях желтыми звездами, излучающими монохроматический свет 570 нм. Стрелки на каждой диаграмме представляют вектор скорости наблюдателя относительно его окружения с величиной 0,89  c .

• В релятивистском случае свет перед наблюдателем смещается в синюю сторону до длины волны 137 нм в дальнем ультрафиолете, а свет позади наблюдателя смещается в красную сторону до 2400 нм в коротковолновом инфракрасном диапазоне. Из-за релятивистской аберрации света объекты, которые ранее находились под прямым углом к ​​наблюдателю, кажутся смещенными вперед на 63°.
• В нерелятивистском случае свет перед наблюдателем смещается в синюю сторону до длины волны 300 нм в среднем ультрафиолете, а свет позади наблюдателя смещается в красную сторону до 5200 нм в промежуточном инфракрасном диапазоне. Из-за аберрации света объекты, которые ранее находились под прямым углом к ​​наблюдателю, кажутся смещенными вперед на 42°.
• В обоих случаях монохроматические звезды впереди и позади наблюдателя смещены Доплером в сторону невидимых длин волн. Однако, если бы у наблюдателя были глаза, которые могли бы видеть в ультрафиолетовом и инфракрасном диапазонах, он бы увидел звезды впереди себя более яркими и более тесно сгруппированными, чем звезды позади, но звезды были бы намного ярче и намного более сконцентрированными в релятивистском случае. ^[13]

Реальные звезды не монохроматичны, а излучают диапазон длин волн, приближающийся к распределению черного тела . Не обязательно, что звезды перед наблюдателем будут иметь более синий цвет. Это происходит потому, что все спектральное распределение энергии смещено. В то же время, когда видимый свет смещается в синюю сторону в невидимые ультрафиолетовые длины волн, инфракрасный свет смещается в синюю сторону в видимый диапазон. Какие именно изменения в цветах мы видим, зависит от физиологии человеческого глаза и от спектральных характеристик наблюдаемых источников света. ^{[14] [15]}

Эффект Доплера на интенсивность

Эффект Доплера (с произвольным направлением) также изменяет воспринимаемую интенсивность источника: это можно кратко выразить тем фактом, что интенсивность источника, деленная на куб частоты, является инвариантом Лоренца ^{[стр. 6] [примечание 2]} Это означает, что общая интенсивность излучения (суммированная по всем частотам) умножается на четвертую степень коэффициента Доплера для частоты.

Вследствие этого, поскольку закон Планка описывает излучение черного тела как имеющее спектральную интенсивность по частоте, пропорциональную (где — температура источника, а частота), мы можем сделать вывод, что спектр черного тела, наблюдаемый через доплеровский сдвиг (с произвольным направлением), по-прежнему является спектром черного тела с температурой, умноженной на тот же коэффициент Доплера, что и частота. ${\displaystyle {\frac {f^{3}}{e^{\frac {hf}{kT}}-1}}}$ ${\displaystyle T}$ ${\displaystyle f}$

Этот результат является одним из доказательств, позволяющих отличить теорию Большого взрыва от альтернативных теорий, предложенных для объяснения космологического красного смещения . ^[16]

Экспериментальная проверка

Поскольку поперечный эффект Доплера является одним из основных новых предсказаний специальной теории относительности, обнаружение и точная количественная оценка этого эффекта стали важной целью экспериментов, направленных на проверку специальной теории относительности.

Измерения типа Айвса и Стилвелла

Рисунок 9. Почему сложно точно измерить поперечный эффект Доплера с помощью поперечного пучка.

Эйнштейн (1907) первоначально предположил, что TDE можно измерить, наблюдая за пучком « каналовых лучей » под прямым углом к ​​пучку. ^{[стр. 1]} Попытки измерить TDE по этой схеме оказались непрактичными, поскольку максимальная скорость пучка частиц, доступная в то время, составляла всего несколько тысячных скорости света.

На рис. 9 показаны результаты попытки измерить линию 4861 ангстрем, испускаемую пучком канальных лучей (смесь ионов H1+, H2+ и H3+), когда они рекомбинируют с электронами, оторванными от разбавленного водородного газа, используемого для заполнения канальной лучевой трубки. Здесь предсказанный результат TDE — линия 4861,06 ангстрем. Слева продольный доплеровский сдвиг приводит к расширению линии излучения до такой степени, что TDE невозможно наблюдать. Средние рисунки иллюстрируют, что даже если сузить поле зрения до точного центра пучка, очень малые отклонения пучка от точного прямого угла вносят сдвиги, сопоставимые с предсказанным эффектом.

Вместо того, чтобы попытаться напрямую измерить TDE, Айвз и Стилвелл (1938) использовали вогнутое зеркало, которое позволило им одновременно наблюдать почти продольный прямой луч (синий) и его отраженное изображение (красный). Спектроскопически можно было бы наблюдать три линии: несмещенную линию излучения и смещенные в синюю и красную области. Среднее значение смещенных в красную и смещенную в синюю области линий можно было бы сравнить с длиной волны несмещенной линии излучения. Разница, которую измерили Айвз и Стилвелл, соответствовала, в пределах экспериментальных ограничений, эффекту, предсказанному специальной теорией относительности. ^{[стр. 7]}

Различные последующие повторения эксперимента Айвза и Стилвелла приняли другие стратегии для измерения среднего значения смещенных в синюю и красную сторону излучений пучка частиц. В некоторых недавних повторениях эксперимента современная ускорительная технология использовалась для организации наблюдения двух противоположно вращающихся пучков частиц. В других повторениях энергии гамма-лучей, испускаемых быстро движущимся пучком частиц, измерялись под противоположными углами относительно направления пучка частиц. Поскольку эти эксперименты фактически не измеряют длину волны пучка частиц под прямым углом к ​​пучку, некоторые авторы предпочли называть измеряемый ими эффект «квадратичным доплеровским сдвигом», а не TDE. ^{[стр. 8] [стр. 9]}

Прямое измерение поперечного эффекта Доплера

Появление технологии ускорителей частиц сделало возможным производство пучков частиц значительно более высокой энергии, чем было доступно Айвсу и Стилвеллу. Это позволило разработать тесты поперечного эффекта Доплера непосредственно по тем направлениям, как изначально представлял их Эйнштейн, т. е. путем непосредственного наблюдения пучка частиц под углом 90°. Например, Хасселькамп и др. (1979) наблюдали линию H α, излучаемую атомами водорода, движущимися со скоростями в диапазоне от 2,53×10 ⁸  см/с до 9,28×10 ⁸  см/с, найдя коэффициент второго порядка в релятивистском приближении равным 0,52±0,03, что прекрасно согласуется с теоретическим значением 1/2. ^{[стр. 10]}

Другие прямые испытания TDE на вращающихся платформах стали возможны благодаря открытию эффекта Мёссбауэра , который позволяет производить чрезвычайно узкие резонансные линии для испускания и поглощения ядерного гамма-излучения. ^[17] Эксперименты с эффектом Мёссбауэра доказали свою способность легко обнаруживать TDE, используя относительные скорости излучателя-поглотителя порядка 2×10 ⁴  см/с. Эти эксперименты включают эксперименты, проведенные Хэем и др. (1960), ^{[стр. 11],} Шампени и др. (1965), ^{[стр. 12]} и Кюндигом (1963). ^{[стр. 3]}

Измерения замедления времени

Поперечный эффект Доплера и кинематическое замедление времени специальной теории относительности тесно связаны. Все подтверждения TDE представляют собой подтверждения кинематического замедления времени, и большинство подтверждений кинематического замедления времени также представляли собой подтверждения TDE. Онлайн-ресурс «Какова экспериментальная основа специальной теории относительности?» задокументировал, с краткими комментариями, многие из тестов, которые на протяжении многих лет использовались для подтверждения различных аспектов специальной теории относительности. ^[18] Кайвола и др. (1985) ^{[стр. 13]} и МакГоуэн и др. (1993) ^{[стр. 14]} являются примерами экспериментов, классифицированных в этом ресурсе как эксперименты по замедлению времени. Эти два также представляют собой тесты TDE. В этих экспериментах сравнивалась частота двух лазеров, один из которых был привязан к частоте перехода атома неона в быстром пучке, а другой — к тому же переходу в тепловом неоне. Версия эксперимента 1993 года подтвердила замедление времени и, следовательно, TDE с точностью 2,3× ¹⁰⁻⁶ .

Релятивистский эффект Доплера для звука и света

Рисунок 10. Релятивистская формула доплеровского сдвига применима как к звуку, так и к свету.

Учебники физики для первого года обучения почти всегда анализируют доплеровский сдвиг для звука в терминах ньютоновской кинематики, в то время как доплеровский сдвиг для света и электромагнитных явлений анализируют в терминах релятивистской кинематики. Это создает ложное впечатление, что акустические явления требуют иного анализа, чем свет и радиоволны.

Традиционный анализ эффекта Доплера для звука представляет собой приближение с низкой скоростью к точному релятивистскому анализу. Полностью релятивистский анализ для звука, по сути, в равной степени применим как к звуковым, так и к электромагнитным явлениям.

Рассмотрим пространственно-временную диаграмму на рис. 10. На этой диаграмме показаны мировые линии для камертона (источника) и приемника. Камертон и приемник начинаются в точке O, в которой камертон начинает вибрировать, испуская волны и двигаясь вдоль отрицательной оси x, в то время как приемник начинает двигаться вдоль положительной оси x. Камертон продолжает движение до тех пор, пока не достигнет точки A, в которой он перестает испускать волны: таким образом, генерируется волновой пакет, и все волны в волновом пакете принимаются приемником, а последняя волна достигает его в точке B. Собственное время для длительности пакета в системе отсчета камертона — это длина OA, в то время как собственное время для длительности волнового пакета в системе отсчета приемника — это длина OB. Если бы волны были испущены, то , в то время как ; обратный наклон AB представляет скорость распространения сигнала (т. е. скорость звука) до события B . Поэтому мы можем записать: ^[10] ${\displaystyle n}$ ${\displaystyle f_{s}={\frac {n}{|OA|}}}$ ${\displaystyle f_{r}={\frac {n}{|OB|}}}$

${\displaystyle c_{s}={\frac {x_{B}-x_{A}}{t_{B}-t_{A}}}}$(скорость звука)

${\displaystyle v_{s}=-{\frac {x_{A}}{t_{A}}}}$        ${\displaystyle v_{r}={\frac {x_{B}}{t_{B}}}}$      (скорости источника и приемника)

${\displaystyle |OA|={\sqrt {t_{A}^{2}-(x_{A}/c)^{2}}}}$

${\displaystyle |OB|={\sqrt {t_{B}^{2}-(x_{B}/c)^{2}}}}$

${\displaystyle v_{s}}$и предполагается, что они меньше, чем, поскольку в противном случае их прохождение через среду вызовет ударные волны, что сделает расчет недействительным. Некоторая рутинная алгебра дает отношение частот: ${\displaystyle v_{r}}$ ${\displaystyle c_{s},}$

Ур. 9:    ${\displaystyle {\frac {f_{r}}{f_{s}}}={\frac {|OA|}{|OB|}}}$ ${\displaystyle ={\frac {1-v_{r}/c_{s}}{1+v_{s}/c_{s}}}{\sqrt {\frac {1-(v_{s}/c)^{2}}{1-(v_{r}/c)^{2}}}}}$

Если и малы по сравнению с , то приведенное выше уравнение сводится к классической формуле Доплера для звука. ${\displaystyle v_{r}}$ ${\displaystyle v_{s}}$ ${\displaystyle c}$

Если скорость распространения сигнала приближается к , можно показать, что абсолютные скорости и источника и приемника сливаются в одну относительную скорость, независимую от какой-либо ссылки на неподвижную среду. Действительно, мы получаем Уравнение 1 , формулу для релятивистского продольного доплеровского сдвига. ^[10] ${\displaystyle c_{s}}$ ${\displaystyle c}$ ${\displaystyle v_{s}}$ ${\displaystyle v_{r}}$

Анализ пространственно-временной диаграммы на рис. 10 дал общую формулу для источника и приемника, движущихся прямо вдоль линии их зрения, т.е. в коллинеарном движении.

Рисунок 11. Источник и приемник движутся в разных направлениях и скоростях в системе отсчета, где скорость звука не зависит от направления.

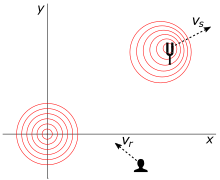
Рис. 11 иллюстрирует сценарий в двух измерениях. Источник движется со скоростью (в момент излучения). Он испускает сигнал, который движется со скоростью к приемнику, который движется со скоростью в момент приема. Анализ выполняется в системе координат, в которой скорость сигнала не зависит от направления. ^[6] ${\displaystyle \mathbf {v_{s}} }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle \mathbf {v_{r}} }$ ${\displaystyle |\mathbf {C} |}$

Соотношение между собственными частотами источника и приемника равно

Ур. 10:    ${\displaystyle {\frac {f_{r}}{f_{s}}}={\frac {1-{\frac {|\mathbf {v_{r}} |}{\mathbf {|C|} }}\cos(\theta _{\mathbf {C,v_{r}} })}{1-{\frac {|\mathbf {v_{s}} |}{\mathbf {|C|} }}\cos(\theta _{\mathbf {C,v_{s}} })}}{\sqrt {\frac {1-(v_{s}/c)^{2}}{1-(v_{r}/c)^{2}}}}}$

Ведущее отношение имеет форму классического эффекта Доплера, в то время как квадратный корень представляет собой релятивистскую поправку. Если мы рассмотрим углы относительно рамки источника, то и уравнение сводится к Уравнению 7 , формуле Эйнштейна 1905 года для эффекта Доплера. Если мы рассмотрим углы относительно рамки приемника, то и уравнение сводится к Уравнению 6 , альтернативной форме уравнения сдвига Доплера, обсуждавшегося ранее. ^[6] ${\displaystyle v_{s}=0}$ ${\displaystyle v_{r}=0}$

Смотрите также

• эффект Доплера
• Дифференциальный эффект Доплера
• Релятивистское излучение
• Красное смещение
• Синее смещение
• Замедление времени
• Гравитационное замедление времени
• Специальная теория относительности

Примечания

1. В своей основополагающей статье 1905 года, вводящей специальную теорию относительности, Эйнштейн уже опубликовал выражение для доплеровского сдвига, воспринимаемого наблюдателем, движущимся под произвольным углом по отношению к бесконечно удаленному источнику света. Вывод Эйнштейном в 1907 году TDE представлял собой тривиальное следствие его ранее опубликованного общего выражения. ^{[стр. 2]}
2. Здесь «сила источника» относится к спектральной интенсивности в частоте , т. е. мощности на единицу телесного угла и на единицу частоты, выраженной в ваттах на стерадиан на герц; для спектральной интенсивности в длине волны куб следует заменить пятой степенью.

Первичные источники

1. Эйнштейн, Альберт (1907). «О возможности нового испытания принципа относительности (Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips)». Аннален дер Физик . 328 (6): 197–198. Бибкод : 1907АнП...328..197Е. дои : 10.1002/andp.19073280613.
2. Эйнштейн, Альберт (1905). «Zur Elektrodynamic bewegter Körper». Аннален дер Физик (на немецком языке). 322 (10): 891–921. Бибкод : 1905АнП...322..891Е. дои : 10.1002/andp.19053221004 .Русский перевод: «К электродинамике движущихся тел»
3. Kündig, Walter (1963). «Измерение поперечного эффекта Доплера в ускоренной системе». Physical Review . 129 (6): 2371–2375. Bibcode : 1963PhRv..129.2371K. doi : 10.1103/PhysRev.129.2371.
4. Champeney, DC; Moon, PB (1961). «Отсутствие доплеровского сдвига для источника гамма-излучения и детектора на одной круговой орбите». Proc. Phys. Soc . 77 (2): 350–352. Bibcode : 1961PPS....77..350C. doi : 10.1088/0370-1328/77/2/318.
5. Синг, Дж. Л. (1963). «Групповые движения в пространстве-времени и эффекты Доплера». Nature . 198 (4881): 679. Bibcode :1963Natur.198..679S. doi : 10.1038/198679a0 . S2CID  42033531.
6. Джонсон, Монтгомери Х.; Теллер, Эдвард (февраль 1982 г.). "Изменения интенсивности в эффекте Доплера". Proc. Natl. Acad. Sci. USA . 79 (4): 1340. Bibcode :1982PNAS...79.1340J. doi : 10.1073/pnas.79.4.1340 . PMC 345964 . PMID  16593162. 
7. Айвс, Х. Э.; Стилвелл, Г. Р. (1938). «Экспериментальное исследование скорости движущихся атомных часов». Журнал оптического общества Америки . 28 (7): 215. Bibcode : 1938JOSA...28..215I. doi : 10.1364/JOSA.28.000215.
8. Олин, А.; Александр, ТК; Хауссер, О.; Макдональд, АБ; Эван, ГТ (1973). «Измерение релятивистского эффекта Доплера с использованием 8,6-МэВ захватных γ-лучей». Phys. Rev. D. 8 ( 6): 1633–1639. Bibcode : 1973PhRvD...8.1633O. doi : 10.1103/PhysRevD.8.1633.
9. Мандельберг, Хирш И.; Виттен, Луис (1962). «Экспериментальная проверка релятивистского эффекта Доплера». Журнал оптического общества Америки . 52 (5): 529–535. Bibcode : 1962JOSA...52..529M. doi : 10.1364/JOSA.52.000529.
10. Хасселькамп, Д.; Мондри, Э.; Шарманн, А. (1979). «Прямое наблюдение поперечного доплеровского сдвига». Zeitschrift für Physik A. 289 (2): 151–155. Бибкод : 1979ZPhyA.289..151H. дои : 10.1007/BF01435932. S2CID  120963034.
11. Hay, HJ; Schiffer, JP; Cranshaw, TE; Egelstaff, PA (1960). «Измерение красного смещения в ускоренной системе с использованием эффекта Мёссбауэра в ⁵⁷ Fe». Physical Review Letters . 4 (4): 165–166. Bibcode : 1960PhRvL...4..165H. doi : 10.1103/PhysRevLett.4.165.
12. Champeney, DC; Isaak, GR; Khan, AM (1965). «Эксперимент по замедлению времени на основе эффекта Мёссбауэра». Труды Физического общества . 85 (3): 583–593. Bibcode : 1965PPS....85..583C. doi : 10.1088/0370-1328/85/3/317.
13. Кайвола, Матти; Риис, Эрлинг; Ли, Сиу Ау (1985). «Измерение релятивистского доплеровского сдвига в неоне» (PDF) . Phys. Rev. Lett . 54 (4): 255–258. Bibcode :1985PhRvL..54..255K. doi :10.1103/PhysRevLett.54.255. PMID  10031461.
14. МакГоуэн, Роджер В.; Гилтнер, Дэвид М.; Стернберг, Скотт Дж.; Ли, Сиу Ау (1993). «Новое измерение релятивистского доплеровского сдвига в неоне». Phys. Rev. Lett . 70 (3): 251–254. Bibcode :1993PhRvL..70..251M. doi :10.1103/PhysRevLett.70.251. PMID  10054065.

Ссылки

1. Дэниел Кифер (2014). Релятивистские электронные зеркала: из взаимодействия высокоинтенсивного лазера с нанофольгой (иллюстрированное издание). Springer. стр. 22. ISBN 978-3-319-07752-9.Выдержка из страницы 22
2. Шер, Д. (1968). «Релятивистский эффект Доплера». Журнал Королевского астрономического общества Канады . 62 : 105–111. Bibcode : 1968JRASC..62..105S . Получено 11 октября 2018 г.
3. Gill, TP (1965). Эффект Доплера . Лондон: Logos Press Limited. С. 6–9. OL  5947329M.
4. Фейнман, Ричард П .; Лейтон, Роберт Б.; Сэндс , Мэтью (февраль 1977 г.). «Релятивистские эффекты в излучении». Лекции Фейнмана по физике: том 1. Рединг, Массачусетс: Addison-Wesley . стр. 34–7 f. ISBN 9780201021165. LCCN  2010938208.
5. Морин, Дэвид (2008). "Глава 11: Относительность (Кинематика)" (PDF) . Введение в классическую механику: с проблемами и решениями . Cambridge University Press . стр. 539–543. ISBN 978-1-139-46837-4. Архивировано из оригинала (PDF) 4 апреля 2018 года.
6. Brown, Kevin S. "The Doppler Effect". Mathpages . Получено 12 октября 2018 г.
7. Мизнер, CW, Торн, KS, и Уилер, J. A (1973). Гравитация . Freeman. стр. 163. ISBN 978-0716703440.{{cite book}}: CS1 maint: multiple names: authors list (link)
8. Sama, Nicholas (1969). "Некоторые комментарии к эксперименту по релятивистскому сдвигу частоты в Шампани и Муне". American Journal of Physics . 37 (8): 832–833. Bibcode : 1969AmJPh..37..832S. doi : 10.1119/1.1975859.
9. Keswani, GH (1965). Origin and Concept of Relativity. Дели, Индия: Alekh Prakashan. стр. 60–61 . Получено 13 октября 2018 г.
10. Браун, Кевин С. "Доплеровский сдвиг для звука и света". Mathpages . Получено 6 августа 2015 г.
11. Ландау, Л. Д.; Лифшиц , Э. М. (2005). Классическая теория полей . Курс теоретической физики: Том 2. Перевод Мортона Хамермеша (Четвертое пересмотренное английское издание). Elsevier Butterworth-Heinemann. С. 116–117. ISBN 9780750627689.
12. Ta-Pei Cheng (2013). Физика Эйнштейна: атомы, кванты и относительность - выведенные, объясненные и оцененные (иллюстрированное, переизданное издание). OUP Oxford. стр. 164. ISBN 978-0-19-966991-2.Выдержка из страницы 164
13. Savage, CM; Searle, AC (1999). "Visualizing Special Relativity" (PDF) . The Physicist . 36 (141). Архивировано из оригинала (PDF) 2008-08-03 . Получено 17 октября 2018 .
14. Брандекер, Алексис. «Что увидел бы релятивистский межзвездный путешественник?». FAQ по физике . Математический факультет Калифорнийского университета, Риверсайд. Архивировано из оригинала 7 мая 2021 г. Получено 17 октября 2018 г.
15. Краус, У. (2000). «Яркость и цвет быстро движущихся объектов: пересмотр визуального образа большой сферы» (PDF) . Am. J. Phys . 68 (1): 56–60. Bibcode :2000AmJPh..68...56K. doi :10.1119/1.19373 . Получено 17 октября 2018 г. .
16. Райт, Эдвард Л. («Нед»). «Ошибки в космологии уставшего света». Учебник космологии Неда Райта . Кафедра астрономии, Калифорнийский университет, Лос-Анджелес . Получено 17 октября 2018 г.
17. Сабуро Насу (2013). «Общее введение в мёссбауэровскую спектроскопию». В Yoshida, Yutaka; Langouche, Guido (ред.). Мёссбауэровская спектроскопия: Учебное пособие . Springer. стр. 1–22. ISBN 978-3642322198.
18. Робертс, Том; Шлейф, Зигмар. «Какова экспериментальная основа специальной теории относительности?». Оригинальный Usenet Physics FAQ . Кафедра математики, Калифорнийский университет, Риверсайд . Получено 16 октября 2018 г.

Дальнейшее чтение

• Moriconi, M (1 ноября 2006 г.). «Специальная теория относительности через эффект Доплера». European Journal of Physics . 27 (6): 1409–1423. arXiv : physics/0605204 . Bibcode : 2006EJPh...27.1409M. doi : 10.1088/0143-0807/27/6/015. S2CID  11347287.

Внешние ссылки

• Warp Special Relativity Simulator — компьютерная программа, демонстрирующая релятивистский эффект Доплера.
• Kraus, Ute; Zahn, Corvin. «Путешествие во времени и пространстве: Визуализация теории относительности». SpacetimeTravel.org . Группа образования в области физики и астрономии, Университет Хильдесхайма, Германия . Получено 17 октября 2018 г. .