Экзистенциальный граф — это тип диаграммной или визуальной записи логических выражений, созданный Чарльзом Сандерсом Пирсом , который писал о графической логике еще в 1882 году [1] и продолжал развивать этот метод до своей смерти в 1914 году. Они включают в себя как отдельную графическую запись для логических утверждений, так и логическое исчисление — формальную систему правил вывода, которая может использоваться для вывода теорем.
Пирс считал, что алгебраическая нотация (т. е. символическая нотация) логики, особенно логики предикатов [2] , которая была еще совсем новой при его жизни и в разработке которой он сам сыграл важную роль, философски неудовлетворительна, поскольку символы имели свое значение просто по соглашению. Напротив, он стремился к стилю письма, в котором знаки буквально несут свое значение внутри себя [3] – в терминологии его теории знаков: система иконических знаков, которые напоминают или напоминают представленные объекты и отношения. [4]
Таким образом, разработка знаковой, графической и – как он и предполагал – интуитивной и простой в изучении логической системы была проектом, над которым Пирс работал всю свою жизнь. После по крайней мере одного прерванного подхода – «Entitative Graphs» – закрытая система «Existential Graphs» наконец появилась с 1896 года. Хотя их создатель считал их явно превосходящей и более интуитивной системой, как способ письма и как исчисление, они не оказали большого влияния на историю логики. Это было приписано тому факту(ам), что, во-первых, Пирс мало публиковал по этой теме и что опубликованные тексты были написаны не очень понятным образом; [5] и, во-вторых, что линейная формульная нотация в руках экспертов на самом деле является менее сложным инструментом. [6] Следовательно, экзистенциальные графы получили мало внимания [7] или считались громоздкими. [8] Начиная с 1963 года, работы Дона Д. Робертса и Дж. Джея Земана, в которых графические системы Пирса были систематически исследованы и представлены, привели к лучшему пониманию; тем не менее, сегодня они нашли практическое применение только в одном современном приложении — концептуальных графах, введенных Джоном Ф. Совой в 1976 году, которые используются в компьютерной науке для представления знаний. Однако экзистенциальные графы все чаще появляются как предмет исследования в связи с растущим интересом к графической логике, [9] что также выражается в попытках заменить правила вывода, данные Пирсом, более интуитивными. [10]
Общая система экзистенциальных графов состоит из трех подсистем, которые строятся друг на друге: альфа-графов, бета-графов и гамма-графов. Альфа-графы являются чисто пропозициональной логической системой. Основываясь на этом, бета-графы являются логическим исчислением первого порядка. Гамма-графы, которые еще не были полностью исследованы и не были завершены Пирсом, понимаются как дальнейшее развитие альфа- и бета-графов. При соответствующей интерпретации гамма-графы охватывают логику предикатов более высокого уровня, а также модальную логику. Еще в 1903 году Пирс начал новый подход, «Окрашенные экзистенциальные графы», с помощью которых он хотел заменить предыдущие системы альфа-, бета- и гамма-графов и объединить их выразительность и производительность в одной новой системе. Как и гамма-графы, «Окрашенные экзистенциальные графы» остались незавершенными.
Как исчисления, альфа-, бета- и гамма-графы являются верными (т. е. все выражения, полученные как графы, семантически допустимы). Альфа- и бета-графы также являются полными (т. е. все пропозициональные или предикатно-логически семантически допустимые выражения могут быть получены как альфа- или бета-графы). [11]
Пирс предложил три системы экзистенциальных графов:
Альфа вложена в бету и гамму . Бета не вложена в гамму , квантифицированная модальная логика является более общей, чем предложенная Пирсом.
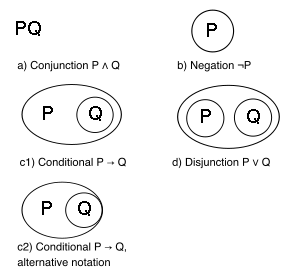
Синтаксис следующий :
Любая правильно сформированная часть графа является подграфом .
Семантика такова :
Следовательно, альфа -графы являются минималистской нотацией для сентенциальной логики , основанной на выразительной адекватности И и Не . Альфа -графы представляют собой радикальное упрощение двухэлементной булевой алгебры и функторов истинности .
Глубина объекта — это количество разрезов, которые его охватывают .
Правила вывода :
Правила эквивалентности :
Доказательство манипулирует графом с помощью ряда шагов, каждый из которых оправдывается одним из приведенных выше правил. Если граф можно свести шагами к чистой странице или пустому разрезу, то это то, что сейчас называется тавтологией ( или ее дополнением, противоречием). Графы, которые нельзя упростить дальше определенной точки, являются аналогами выполнимых формул логики первого порядка .


В случае бетаграфов атомарные выражения больше не являются пропозициональными буквами (P, Q, R,...) или утверждениями («Идет дождь», «Пирс умер в нищете»), а предикатами в смысле логики предикатов (см. там для получения более подробной информации), возможно, сокращенными до предикатных букв (F, G, H,...). Предикат в смысле логики предикатов — это последовательность слов с четко определенными пробелами, которая становится пропозициональным предложением, если в каждый пробел вставить имя собственное. Например, последовательность слов «_ x is a human» является предикатом, поскольку она порождает повествовательное предложение «Пирс is a human», если в пустое место вставить имя собственное «Пирс». Аналогично, последовательность слов «_ 1 is richer than _ 2 » является предикатом, поскольку она приводит к утверждению «Сократ is richer than Plato», если в пробелы вставить имена собственные «Сократ» или «Платон».
Базовый языковой прием — линия идентичности, жирно нарисованная линия любой формы. Линия идентичности прикрепляется к пустому месту предиката, чтобы показать, что предикат применяется по крайней мере к одному индивиду. Чтобы выразить, что предикат «_ is a human being» применяется по крайней мере к одному индивиду, т. е. сказать, что существует (по крайней мере) один человек, в пустом месте предиката «_ is a human being» пишется линия идентичности:
Бета-графики можно читать как систему, в которой все формулы следует считать закрытыми, поскольку все переменные неявно квантифицированы. Если «самая мелкая» часть линии идентичности имеет четную глубину, то соответствующая переменная неявно экзистенциально ( универсально ) квантифицирована.
Zeman (1964) был первым, кто заметил, что бета- графы изоморфны логике первого порядка с равенством (см. также Zeman 1967). Однако вторичная литература, особенно Roberts (1973) и Shin (2002), не соглашаются с тем, как это происходит. Работы Пирса не затрагивают этот вопрос, поскольку логика первого порядка была впервые четко сформулирована только после его смерти, в первом издании 1928 года « Принципов математической логики» Дэвида Гильберта и Вильгельма Аккермана .
Добавьте к синтаксису альфа второй вид простой замкнутой кривой , записанной с использованием пунктирной, а не сплошной линии. Пирс предложил правила для этого второго стиля разреза, который можно прочитать как примитивный унарный оператор модальной логики .
Земан (1964) был первым, кто заметил, что гамма -графы эквивалентны известным модальным логикам S4 и S5 . Следовательно, гамма -графы можно рассматривать как своеобразную форму нормальной модальной логики . Это открытие Земана до сих пор не получило должного внимания, но тем не менее включено сюда как интересный момент.
Экзистенциальные графы являются любопытным потомком Пирса, логика / математика, а Пирс был основателем крупного направления семиотики . Графическая логика Пирса — лишь одно из его многочисленных достижений в логике и математике. В серии статей, начавшихся в 1867 году и завершившихся его классической статьей в Американском журнале математики 1885 года , Пирс разработал большую часть двухэлементной булевой алгебры , пропозиционального исчисления , квантификации и исчисления предикатов , а также некоторую элементарную теорию множеств . Теоретики моделей считают Пирса первым в своем роде. Он также расширил алгебру отношений Де Моргана . Он остановился на металогике (которая ускользнула даже от Principia Mathematica ).
Но развивающаяся семиотическая теория Пирса привела его к сомнению ценности логики, сформулированной с использованием обычной линейной нотации, и к предпочтению, чтобы логика и математика были записаны в двух (или даже трех) измерениях. Его работа вышла за рамки диаграмм Эйлера и их пересмотра Венном 1880 года . Работа Фреге 1879 года Begriffsschrift также использовала двумерную нотацию для логики, но сильно отличающуюся от нотации Пирса.
Первая опубликованная работа Пирса по графической логике (перепечатанная в томе 3 его Сборника статей ) предложила систему, двойственную (по сути) к альфа- экзистенциальным графам, названную сущностными графами . Он очень скоро отказался от этого формализма в пользу экзистенциальных графов. В 1911 году Виктория, леди Уэлби показала экзистенциальные графы К. К. Огдену , который посчитал, что их можно было бы с пользой объединить с мыслями Уэлби в «менее абстрагированной форме». [12] В остальном они привлекали мало внимания при его жизни и неизменно принижались или игнорировались после его смерти, вплоть до докторских диссертаций Робертса (1964) и Земана (1964).
В настоящее время хронологическое критическое издание работ Пирса, Writings , охватывает только 1892 год. Большая часть работы Пирса по логическим графам состоит из рукописей, написанных после этой даты и до сих пор не опубликованных. Поэтому наше понимание графической логики Пирса, вероятно, изменится по мере появления оставшихся 23 томов хронологического издания.