Локсодромальная линия

Arc crossing all meridians of longitude at the same angle

Изображение локсодромии, или локсодромии, спирально направленной к Северному полюсу.

В навигации , локсодромия , румб ( / r ʌ m / ) или локсодромия - это дуга, пересекающая все меридианы долготы под одним и тем же углом , то есть путь с постоянным азимутом ( направлением , измеренным относительно истинного севера ). Навигация по фиксированному курсу ( то есть управление судном для следования в постоянном направлении по стороне света ) приведет к траектории локсодромии .

Введение

Эффект следования курсу локсодромии на поверхности глобуса впервые был рассмотрен португальским математиком Педру Нунесом в 1537 году в его «Трактате в защиту морской карты» , а дальнейшее математическое развитие этой идеи было осуществлено Томасом Харриотом в 1590-х годах.

Локсодромию можно противопоставить большому кругу , который является путем кратчайшего расстояния между двумя точками на поверхности сферы. На большом круге пеленг к точке назначения не остается постоянным. Если бы кто-то вел машину по большому кругу, он бы держал руль неподвижно, но чтобы следовать по локсодромии, ему пришлось бы поворачивать руль, поворачивая его более резко по мере приближения к полюсам. Другими словами, большой круг локально «прямой» с нулевой геодезической кривизной , тогда как локсодромия имеет ненулевую геодезическую кривизну.

Меридианы долготы и параллели широты представляют собой особые случаи локсодромии, где их углы пересечения составляют соответственно 0° и 90°. При прохождении с севера на юг курс локсодромии совпадает с большим кругом, как и при прохождении с востока на запад вдоль экватора .

На карте проекции Меркатора любая локсодромия является прямой линией; локсодромию можно провести на такой карте между любыми двумя точками на Земле, не выходя за край карты. Но теоретически локсодромия может простираться за правый край карты, где она затем продолжается на левом краю с тем же наклоном (предполагая, что карта покрывает ровно 360 градусов долготы).

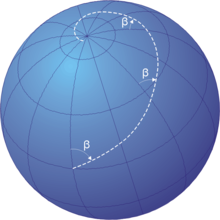
Румбовые линии, пересекающие меридианы под косыми углами, являются локсодромическими кривыми, которые закручиваются по спирали к полюсам. ^[1] На проекции Меркатора Северный и Южный полюсы находятся в бесконечности и поэтому никогда не отображаются. Однако полная локсодромия на бесконечно высокой карте состояла бы из бесконечного числа линейных сегментов между двумя краями. На карте стереографической проекции локсодромия представляет собой равноугольную спираль , центром которой является северный или южный полюс.

Все локсодромии спиралевидны от одного полюса к другому. Вблизи полюсов они близки к логарифмическим спиралям (которыми они являются в точности на стереографической проекции , см. ниже), поэтому они обвиваются вокруг каждого полюса бесконечное число раз, но достигают полюса на конечном расстоянии. Длина локсодромии от полюса до полюса (предполагая идеальную сферу ) — это длина меридиана , деленная на косинус пеленга от истинного севера. Локсодромии не определены на полюсах.

• Три вида локсодромии от полюса к полюсу

Этимология и историческое описание

Слово локсодром происходит от древнегреческого λοξός loxós : «косой» + δρόμος drómos : «бег» (от δραμεῖν drameîn : «бежать»). Слово rhumb может происходить от испанского или португальского rumbo/rumo («курс» или «направление») и греческого ῥόμβος rhómbos , ^[2] от rhémbein .

В издании «The Globe Encyclopaedia of Universal Information» 1878 года линия локсодромии описывается следующим образом: ^[3]

Локсодромическая линия — это кривая, которая пересекает каждый элемент системы линий кривизны данной поверхности под одним и тем же углом. Корабль, плывущий к одной и той же точке компаса, описывает такую ​​линию, которая пересекает все меридианы под одним и тем же углом. В проекции Меркатора (см.) локсодромические линии, очевидно, прямые. ^[3]

Недоразумение могло возникнуть, поскольку термин «румб» не имел точного значения, когда он вошел в употребление. Он одинаково хорошо применялся как к линиям розы ветров , так и к локсодромиям, поскольку этот термин применялся только «локально» и означал только то, что делал моряк, чтобы плыть с постоянным пеленгом , со всей неточностью, которую это подразумевает. Поэтому «румб» применялся к прямым линиям на портоланах, когда портоланы использовались, а также всегда применялся к прямым линиям на картах Меркатора. Для коротких расстояний «румб» портоланов не имеет существенных отличий от румбов Меркатора, но в наши дни «румб» является синонимом математически точного «локсодромии», поскольку он был сделан синонимом ретроспективно. Как утверждает Лео Багроу: ^[4]

слово («Румблина») ошибочно применяется к морским картам этого периода, поскольку локсодромия дает точный курс только тогда, когда карта нарисована на подходящей проекции. Картометрическое исследование показало, что на ранних картах не использовалась никакая проекция, поэтому мы сохраняем для них название «портолан».

Математическое описание

Для сферы радиусом 1 азимутальный угол λ , полярный угол − ⁠π/2⁠ ≤ φ ≤ ⁠π/2⁠ (определено здесь для соответствия широте), и декартовы единичные векторы i , j и k можно использовать для записи радиус-вектора r как

${\displaystyle \mathbf {r} (\lambda ,\varphi )=(\cos {\lambda }\cdot \cos {\varphi })\mathbf {i} +(\sin {\lambda }\cdot \cos {\varphi })\mathbf {j} +(\sin {\varphi })\mathbf {k} \,.}$

Ортогональные единичные векторы в азимутальном и полярном направлениях сферы можно записать

${\displaystyle {\begin{aligned}{\boldsymbol {\hat {\lambda }}}(\lambda ,\varphi )&=\sec {\varphi }{\frac {\partial \mathbf {r} }{\partial \lambda }}=(-\sin {\lambda })\mathbf {i} +(\cos {\lambda })\mathbf {j} \,,\\[8pt]{\boldsymbol {\hat {\varphi }}}(\lambda ,\varphi )&={\frac {\partial \mathbf {r} }{\partial \varphi }}=(-\cos {\lambda }\cdot \sin {\varphi })\mathbf {i} +(-\sin {\lambda }\cdot \sin {\varphi })\mathbf {j} +(\cos {\varphi })\mathbf {k} \,,\end{aligned}}}$

которые имеют скалярные произведения

${\displaystyle {\boldsymbol {\hat {\lambda }}}\cdot {\boldsymbol {\hat {\varphi }}}={\boldsymbol {\hat {\lambda }}}\cdot \mathbf {r} ={\boldsymbol {\hat {\varphi }}}\cdot \mathbf {r} =0\,.}$

λ̂ при постоянном φ определяет параллель широты, тогда как φ̂ при постоянном λ определяет меридиан долготы, и вместе они образуют плоскость, касательную к сфере.

Единичный вектор

${\displaystyle \mathbf {\boldsymbol {\hat {\beta }}} (\lambda ,\varphi )=(\sin {\beta }){\boldsymbol {\hat {\lambda }}}+(\cos {\beta }){\boldsymbol {\hat {\varphi }}}}$

имеет постоянный угол β с единичным вектором φ̂ для любых λ и φ , так как их скалярное произведение равно

${\displaystyle {\boldsymbol {\hat {\beta }}}\cdot {\boldsymbol {\hat {\varphi }}}=\cos {\beta }\,.}$

Локсодромия определяется как кривая на сфере, которая имеет постоянный угол β со всеми меридианами долготы, и поэтому должна быть параллельна единичному вектору β̂ . В результате дифференциальная длина ds вдоль локсодромии даст дифференциальное смещение

${\displaystyle {\begin{aligned}d\mathbf {r} &={\boldsymbol {\hat {\beta }}}\,ds\\[8px]{\frac {\partial \mathbf {r} }{\partial \lambda }}\,d\lambda +{\frac {\partial \mathbf {r} }{\partial \varphi }}\,d\varphi &={\bigl (}(\sin {\beta })\,{\boldsymbol {\hat {\lambda }}}+(\cos {\beta })\,{\boldsymbol {\hat {\varphi }}}{\bigr )}ds\\[8px](\cos {\varphi })\,d\lambda \,{\boldsymbol {\hat {\lambda }}}+d\varphi \,{\boldsymbol {\hat {\varphi }}}&=(\sin {\beta })\,ds\,{\boldsymbol {\hat {\lambda }}}+(\cos {\beta })\,ds\,{\boldsymbol {\hat {\varphi }}}\\[8px]ds&={\frac {\cos {\varphi }}{\sin {\beta }}}\,d\lambda ={\frac {d\varphi }{\cos {\beta }}}\\[8px]{\frac {d\lambda }{d\varphi }}&=\tan {\beta }\cdot \sec {\varphi }\\[8px]\lambda (\varphi \,|\,\beta ,\lambda _{0},\varphi _{0})&=\tan \beta \cdot {\big (}\operatorname {gd} ^{-1}\varphi -\operatorname {gd} ^{-1}\varphi _{0}{\big )}+\lambda _{0}\\[8px]\varphi (\lambda \,|\,\beta ,\lambda _{0},\varphi _{0})&=\operatorname {gd} {\big (}(\lambda -\lambda _{0})\cot \beta +\operatorname {gd} ^{-1}\varphi _{0}{\big )}\end{aligned}}}$

где и — функция Гудермана и обратная ей функция, а — обратный гиперболический синус . ${\displaystyle \operatorname {gd} }$ ${\displaystyle \operatorname {gd} ^{-1}}$ ${\displaystyle \operatorname {gd} \psi =\arctan(\sinh \psi ),}$ ${\displaystyle \operatorname {gd} ^{-1}\varphi =\operatorname {arsinh} (\tan \varphi ),}$ ${\displaystyle \operatorname {arsinh} }$

При таком соотношении между λ и φ радиус-вектор становится параметрической функцией одной переменной, описывающей локсодромию на сфере:

${\displaystyle \mathbf {r} (\lambda \,|\,\beta ,\lambda _{0},\varphi _{0})={\big (}\cos {\lambda }\cdot \operatorname {sech} \psi {\big )}\mathbf {i} +{\big (}\sin {\lambda }\cdot \operatorname {sech} \psi {\big )}\mathbf {j} +{\big (}\tanh \psi {\big )}\mathbf {k} \,,}$

где

${\displaystyle \psi \equiv (\lambda -\lambda _{0})\cot \beta +\operatorname {gd} ^{-1}\varphi _{0}=\operatorname {gd} ^{-1}\varphi }$

это изометрическая широта . ^[5]

В локсодромии, по мере того как широта стремится к полюсам, φ → ± ⁠π/2⁠ , sin φ → ±1 , изометрическая широта ar sinh(tan φ ) → ± ∞ , а долгота λ увеличивается без ограничений, очень быстро вращаясь по спирали вокруг сферы по направлению к полюсу, стремясь к конечной общей длине дуги Δ s , определяемой выражением

${\displaystyle \Delta s=R\,{\big |}(\pm \pi /2-\varphi _{0})\cdot \sec \beta {\big |}}$

Подключение к проекции Меркатора

Локсодром (синяя) в сравнении с дугой большого круга (красная) между Лиссабоном, Португалия и Гаваной, Куба. Вверху: ортографическая проекция. Внизу: проекция Меркатора.

Пусть λ — долгота точки на сфере, а φ — ее широта. Тогда, если мы определим координаты карты проекции Меркатора как

${\displaystyle {\begin{aligned}x&=\lambda -\lambda _{0}\,,\\y&=\operatorname {gd} ^{-1}\varphi =\operatorname {arsinh} (\tan \varphi )\,,\end{aligned}}}$

локсодромия с постоянным направлением β от истинного севера будет прямой линией, поскольку (используя выражение из предыдущего раздела)

${\displaystyle y=mx}$

с уклоном

${\displaystyle m=\cot \beta \,.}$

Найти локсодромии между двумя заданными точками можно графически на карте Меркатора или путем решения нелинейной системы двух уравнений относительно двух неизвестных m = cot β и λ ₀ . Существует бесконечно много решений; кратчайшее из них — то, которое охватывает фактическую разницу долгот, т. е. не делает лишних оборотов и не идет «в обратную сторону».

Расстояние между двумя точками Δ s , измеренное вдоль локсодромии, представляет собой просто абсолютное значение секанса пеленга (азимута), умноженное на расстояние север-юг (за исключением кругов широты , для которых расстояние становится бесконечным):

${\displaystyle \Delta s=R\,{\big |}(\varphi -\varphi _{0})\cdot \sec \beta {\big |}}$

где R — один из средних радиусов Земли .

Приложение

Его использование в навигации напрямую связано со стилем или проекцией определенных навигационных карт. Румбовая линия отображается как прямая линия на карте проекции Меркатора . ^[1]

Название происходит от старофранцузского или испанского соответственно: «rumb» или «rumbo», линия на карте, которая пересекает все меридианы под одним и тем же углом. ^[1] На плоской поверхности это было бы кратчайшее расстояние между двумя точками. Над поверхностью Земли на низких широтах или на коротких расстояниях его можно использовать для построения курса транспортного средства, самолета или корабля. ^[1] На больших расстояниях и/или на более высоких широтах маршрут по дуге большого круга значительно короче, чем локсодромии между теми же двумя точками. Однако неудобство, связанное с необходимостью постоянной смены пеленга во время движения по локсодромии, делает навигацию по локсодромии привлекательной в определенных случаях. ^[1]

Эту точку можно проиллюстрировать с помощью прохода с востока на запад на протяжении 90 градусов долготы вдоль экватора , для которого расстояния по большой окружности и локсодромии одинаковы и составляют 10 000 километров (5 400 морских миль). На 20 градусах северной широты расстояние по большой окружности составляет 9 254 км (4 997 морских миль), а расстояние по локсодромии — 9 397 км (5 074 морских миль), что примерно на 1,5% больше. Но на 60 градусах северной широты расстояние по большой окружности составляет 4 602 км (2 485 морских миль), а расстояние по локсодромии — 5 000 км (2 700 морских миль), разница составляет 8,5%. Более экстремальным случаем является воздушный маршрут между Нью-Йорком и Гонконгом , для которого путь по локсодромии составляет 18 000 км (9 700 морских миль). Длина маршрута по дуге большого круга через Северный полюс составляет 13 000 км (7 000 морских миль), или 5+На 1 ⁄ 2 часа меньше времени полета на типичной крейсерской скорости .

Некоторые старые карты в проекции Меркатора имеют сетки, состоящие из линий широты и долготы , но также показывают локсодромии, которые ориентированы прямо на север, под прямым углом к ​​северу или под некоторым углом к ​​северу, который является некоторой простой рациональной дробью прямого угла. Эти локсодромии будут нарисованы так, чтобы они сходились в определенных точках карты: линии, идущие в каждом направлении, будут сходиться в каждой из этих точек. См. компасную розу . Такие карты обязательно были бы в проекции Меркатора, поэтому не все старые карты могли бы показывать отметки локсодромии.

Радиальные линии на компасной розе также называются румбами . Выражение «плыть по румбу» использовалось в XVI–XIX веках для обозначения определенного направления по компасу. ^[1]

Ранние мореплаватели до изобретения морского хронометра использовали курсы по локсодромии на длинных океанских переходах, потому что широта судна могла быть точно установлена ​​по наблюдению за Солнцем или звездами, но не было точного способа определить долготу. Корабль плыл на север или юг, пока не достигал широты пункта назначения, а затем плыл на восток или запад вдоль локсодромии (на самом деле параллели , которая является частным случаем локсодромии), поддерживая постоянную широту и регулярно записывая оценки пройденного расстояния, пока не показывалась земля. ^[6]

Обобщения

На сфере Римана

Поверхность Земли можно математически понимать как сферу Римана , то есть как проекцию сферы на комплексную плоскость . В этом случае локсодромии можно понимать как определенные классы преобразований Мёбиуса .

Сфероид

Формулировка выше может быть легко расширена до сфероида . ^{[7] [8] [9] [10] [11] [12]} Курс локсодромии находится просто с использованием эллипсоидальной изометрической широты . В формулах выше на этой странице замените конформную широту на эллипсоиде на широту на сфере. Аналогично, расстояния находятся путем умножения длины дуги эллипсоидального меридиана на секанс азимута.

Смотрите также

• Большой круг
• Геодезические на эллипсоиде
• Большой эллипс
• Изоазимутальный
• Сеть рамблайн
• спираль Зейферта
• Малый круг

Ссылки

1. Oxford University Press Rhumb Line. Оксфордский справочник по кораблям и морю, Oxford University Press, 2006. Получено с Encyclopedia.com 18 июля 2009 г.
2. Румб в TheFreeDictionary
3. Ross, JM (редактор) (1878). The Globe Encyclopaedia of Universal Information , том IV, Эдинбург-Шотландия, Thomas C. Jack, Grange Publishing Works, получено из Google Books 2009-03-18;
4. Лео Багроу (2010). История картографии. Transaction Publishers. стр. 65. ISBN 978-1-4128-2518-4.
5. Джеймс Александр, Локсодромы: путь румба, «Mathematics Magazine», том 77. № 5, декабрь 2004 г. [1]
6. Краткая история британской морской мощи, Дэвид Ховарт, изд. Constable & Robinson, Лондон, 2003, глава 8.
7. Смарт, В. М. (1946). «О проблеме навигации». Ежемесячные уведомления Королевского астрономического общества . 106 (2): 124–127. Bibcode : 1946MNRAS.106..124S. doi : 10.1093/mnras/106.2.124 .
8. Уильямс, JED (1950). «Локсодромические расстояния на земном сфероиде». Журнал навигации . 3 (2): 133–140. doi :10.1017/S0373463300045549. S2CID  128651304.
9. Карлтон-Випперн, KC (1992). «О локсодромном мореплавании». Журнал навигации . 45 (2): 292–297. дои : 10.1017/S0373463300010791. S2CID  140735736.
10. Беннетт, ГГ (1996). «Практические вычисления локсодромии на сфероиде». Журнал навигации . 49 (1): 112–119. Bibcode : 1996JNav...49..112B. doi : 10.1017/S0373463300013151. S2CID  128764133.
11. Ботнев, В.А.; Устинов, С.М. (2014). Методы решения прямых и обратных геодезических задач с высокой точностью [Методы решения прямых и обратных геодезических задач с высокой точностью] (PDF) . Вестник Санкт-Петербургского государственного политехнического университета (на русском языке). 3 (198): 49–58.
12. Karney, CFF (2024). "Площадь румбовых полигонов". Studia Geophysica et Geodaetica . 68. doi : 10.1007/s11200-024-0709-z .

Примечание: в данной статье использован текст из издания 1878 года «The Globe Encyclopaedia of Universal Information» , являющегося общественным достоянием.

Дальнейшее чтение

• Монмонье, Марк (2004). Румбы и войны карт. Социальная история проекции Меркатора . Чикаго: Издательство Чикагского университета. ISBN 9780226534329.

Внешние ссылки

• Постоянные заголовки и локсодромные линии на MathPages.
• RhumbSolve(1), утилита для расчета эллипсоидальной локсодромии (компонент GeographicLib).
• Онлайн-версия RhumbSolve.
• Навигационные алгоритмы. Архивировано 16 октября 2018 г. в Wayback Machine Paper: The Sailings.
• Chart Work - Навигационные алгоритмы Chart Work бесплатное программное обеспечение: Локсодромия, Большой круг, Композитное плавание, Меридиональные части. Линии положения Лоцманская лоция - течения и прибрежные координаты.
• Локсодром Mathworld.