линза Люнебурга

Сферически-симметричная градиентная линза

Поперечное сечение стандартной линзы Люнеберга с синим оттенком, пропорциональным показателю преломления.

Линза Люнебурга (в оригинале нем. L ü neburg-Linse ) — сферически-симметричная градиентная линза . Показатель преломления n типичной линзы Люнебурга уменьшается радиально от центра к внешней поверхности. Они могут быть изготовлены для использования с электромагнитным излучением от видимого света до радиоволн .

Для определенных профилей показателя преломления линза будет формировать идеальные геометрические изображения двух заданных концентрических сфер друг на друге. Существует бесконечное число профилей показателя преломления, которые могут производить этот эффект. Простейшее такое решение было предложено Рудольфом Люнебургом в 1944 году. ^[1] Решение Люнебурга для показателя преломления создает два сопряженных фокуса вне линзы. Решение принимает простую и явную форму, если одна фокальная точка лежит на бесконечности, а другая на противоположной поверхности линзы. Дж. Браун и А. С. Гутман впоследствии предложили решения, которые генерируют одну внутреннюю фокальную точку и одну внешнюю фокальную точку. ^{[2] [3]} Эти решения не являются уникальными; набор решений определяется набором определенных интегралов , которые должны быть оценены численно. ^[4]

Дизайны

Решение Люнебурга

Линза Люнеберга преобразует точечный источник в коллимированный пучок , если источник поместить на ее край.

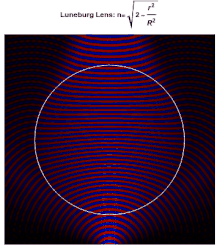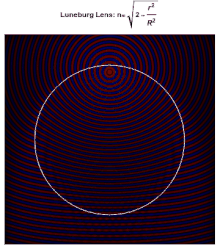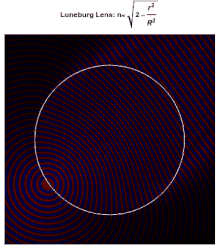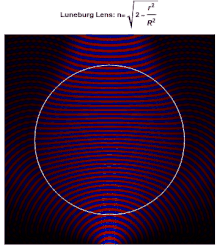
Каждая точка на поверхности идеальной линзы Люнеберга является точкой фокусировки параллельного излучения, падающего на противоположную сторону. В идеале диэлектрическая проницаемость материала, из которого состоит линза, падает с 2 в ее центре до 1 на ее поверхности (или, что эквивалентно, показатель преломления падает с до 1), согласно ${\displaystyle \epsilon _{r}}$ ${\displaystyle n}$ ${\displaystyle {\sqrt {2}}}$

${\displaystyle n={\sqrt {\epsilon _{r}}}={\sqrt {2-\left({\frac {r}{R}}\right)^{2}}},}$

где - радиус линзы. Поскольку показатель преломления на поверхности такой же, как и у окружающей среды, отражения на поверхности не происходит. Внутри линзы траектории лучей представляют собой дуги эллипсов . ${\displaystyle R}$

Рыбий глаз Максвелла

Поперечное сечение линзы Максвелла типа «рыбий глаз», с синим затенением, представляющим увеличение показателя преломления.

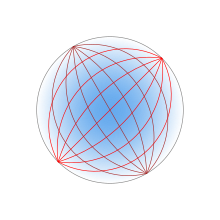
Рыбий глаз Максвелла также является примером обобщенной линзы Люнебурга. Рыбий глаз, который был впервые полностью описан Максвеллом в 1854 году ^[5] (и, следовательно, предшествовал решению Люнебурга), имеет показатель преломления, изменяющийся в соответствии с

${\displaystyle n(r)={\sqrt {\epsilon _{r}}}={\frac {n_{0}}{1+\left({\frac {r}{R}}\right)^{2}}},}$

где — показатель преломления в центре линзы, а — радиус сферической поверхности линзы. ^[6] Показатель преломления на поверхности линзы равен . Линза отображает каждую точку на сферической поверхности в противоположную точку на поверхности. Внутри линзы траектории лучей представляют собой дуги окружностей. ${\displaystyle n_{0}}$ ${\displaystyle R}$ ${\displaystyle n_{0}/2}$

Публикация и атрибуция

Свойства этой линзы описаны в одной из множества задач или головоломок в Cambridge and Dublin Mathematical Journal 1853 года . ^[7] Задача состоит в том, чтобы найти показатель преломления как функцию радиуса, учитывая, что луч описывает круговую траекторию, и далее доказать фокусирующие свойства линзы. Решение дано в издании того же журнала 1854 года. ^[5] Задачи и решения изначально были опубликованы анонимно, но решение этой задачи (и еще одной) было включено в работу Нивена « Научные труды Джеймса Клерка Максвелла» ^[8] , которая была опубликована через 11 лет после смерти Максвелла.

Приложения

На практике линзы Люнебурга обычно представляют собой слоистую структуру из дискретных концентрических оболочек, каждая из которых имеет свой показатель преломления. Эти оболочки образуют ступенчатый профиль показателя преломления, который немного отличается от решения Люнебурга. Этот тип линз обычно используется для микроволновых частот , особенно для построения эффективных микроволновых антенн и стандартов калибровки радаров . Цилиндрические аналоги линзы Люнебурга также используются для коллимации света от лазерных диодов .

Радиолокационный отражатель

Отражатели Люнеберга (отмеченный выступ) на F-35

Из линзы Люнеберга можно изготовить радиолокационный отражатель , металлизировав части ее поверхности. Излучение от удаленного радиолокационного передатчика фокусируется на нижней стороне металлизации на противоположной стороне линзы; здесь оно отражается и фокусируется обратно на радиолокационную станцию. Сложность этой схемы заключается в том, что металлизированные области блокируют вход или выход излучения на этой части линзы, а неметаллизированные области приводят к образованию слепого пятна на противоположной стороне.

Съемные линзовые отражатели радаров Люнебурга иногда прикрепляются к военным самолетам, чтобы сделать невидимые самолеты видимыми во время тренировочных операций или скрыть их истинную радиолокационную сигнатуру. В отличие от других типов отражателей радаров, их форма не влияет на управление самолетом. ^{[9] [10]}

Микроволновая антенна

Трехмерный радар типа 984 на корабле HMS  Victorious , 1961 г., с линзой Люнеберга.

Линза Люнеберга может быть использована в качестве основы высокоусиленной радиоантенны. Эта антенна сравнима с тарелочной антенной , но использует линзу, а не параболический отражатель в качестве основного фокусирующего элемента. Как и в тарелочной антенне, облучатель к приемнику или от передатчика размещается в фокусе, облучатель обычно состоит из рупорной антенны . Фазовый центр облучателя должен совпадать с точкой фокуса, но поскольку фазовый центр неизменно находится несколько внутри устья рупора, его нельзя подвести прямо к поверхности линзы. Следовательно, необходимо использовать разновидность линзы Люнеберга, которая фокусируется несколько за ее поверхностью, ^[11] а не классическую линзу с фокусом, лежащим на поверхности.

Антенна с линзой Люнебурга имеет ряд преимуществ по сравнению с параболической тарелкой. Поскольку линза сферически симметрична, антенной можно управлять, перемещая облучатель вокруг линзы, без необходимости вращать всю антенну. Опять же, поскольку линза сферически симметрична, можно использовать одну линзу с несколькими облучателями, смотрящими в совершенно разных направлениях. Напротив, если несколько облучателей используются с параболическим рефлектором, все они должны находиться в пределах небольшого угла оптической оси , чтобы избежать комы (формы расфокусировки). Помимо офсетных систем, антенны-тарелки страдают от того, что облучатель и его опорная конструкция частично закрывают основной элемент ( блокировка апертуры ); как и другие преломляющие системы, антенна с линзой Люнебурга избегает этой проблемы.

Разновидностью линзовой антенны Люнебурга является полусферическая линзовая антенна Люнебурга или рефлекторная антенна Люнебурга . Она использует только одну полусферу линзы Люнебурга, при этом срезанная поверхность сферы опирается на отражающую металлическую заземляющую плоскость . Такое расположение вдвое уменьшает вес линзы, а заземляющая плоскость обеспечивает удобное средство поддержки. Однако облучатель частично закрывает линзу, когда угол падения на отражатель меньше примерно 45°.

Путь луча внутри линзы

Для любой сферически симметричной линзы каждый луч целиком лежит в плоскости, проходящей через центр линзы. Начальное направление луча определяет линию, которая вместе с центральной точкой линзы определяет плоскость, делящую линзу пополам. Будучи плоскостью симметрии линзы, градиент показателя преломления не имеет компонента, перпендикулярного этой плоскости, который мог бы заставить луч отклониться либо в одну, либо в другую сторону. В плоскости круговая симметрия системы делает удобным использование полярных координат для описания траектории луча. ${\displaystyle (r,\theta )}$

Если взять любые две точки на луче (например, точку входа и выхода из линзы), принцип Ферма утверждает, что путь, который проходит луч между ними, — это тот путь, который он может пройти за наименьшее возможное время. Учитывая, что скорость света в любой точке линзы обратно пропорциональна показателю преломления, и по Пифагору , время прохождения между двумя точками и равно ${\displaystyle (r_{1},\theta _{1})}$ ${\displaystyle (r_{2},\theta _{2})}$

${\displaystyle T=\int _{(r_{1},\theta _{1})}^{(r_{2},\theta _{2})}{\frac {n(r)}{c}}{\sqrt {(r\,d\theta )^{2}+dr^{2}}}={\frac {1}{c}}\int _{\theta _{1}}^{\theta _{2}}n(r){\sqrt {r^{2}+\left({\frac {dr}{d\theta }}\right)^{2}}}\,d\theta ,}$

где — скорость света в вакууме. Минимизация этого дает дифференциальное уравнение второго порядка , определяющее зависимость от вдоль пути луча. Этот тип задачи минимизации широко изучался в механике Лагранжа , и готовое решение существует в форме тождества Бельтрами , которое немедленно дает первый интеграл этого уравнения второго порядка. Подстановка (где представляет ) в это тождество дает ${\displaystyle c}$ ${\displaystyle T}$ ${\displaystyle r}$ ${\displaystyle \theta }$ ${\displaystyle L(r,r')=n(r){\sqrt {r'^{2}+r^{2}}}}$ ${\displaystyle r'}$ ${\displaystyle {\tfrac {dr}{d\theta }}}$

${\displaystyle n(r){\sqrt {r'^{2}+r^{2}}}-n(r){\frac {r'^{2}}{\sqrt {r'^{2}+r^{2}}}}=h,}$

где - константа интегрирования . Это дифференциальное уравнение первого порядка является разделяемым , то есть его можно переставить так, чтобы появлялось только с одной стороны и только с другой: ^[1] ${\displaystyle h}$ ${\displaystyle r}$ ${\displaystyle \theta }$

${\displaystyle d\theta ={\frac {h}{r{\sqrt {{\big (}n(r){\big )}^{2}r^{2}-h^{2}}}}}\,dr.}$

Параметр является константой для любого заданного луча, но отличается для лучей, проходящих на разных расстояниях от центра линзы. Для лучей, проходящих через центр, он равен нулю. В некоторых особых случаях, например, для «рыбьего глаза» Максвелла, это уравнение первого порядка может быть дополнительно интегрировано, чтобы получить формулу для как функцию от . В общем случае оно дает относительные скорости изменения и , которые могут быть численно интегрированы для отслеживания пути луча через линзу. ${\displaystyle h}$ ${\displaystyle \theta }$ ${\displaystyle r}$ ${\displaystyle \theta }$ ${\displaystyle r}$

Смотрите также

• Шаровидная линза
• Спутник BLITS (Шаровая линза в космосе)
• Гравитационные линзы также имеют радиально уменьшающийся показатель преломления.

Ссылки

1. Luneburg, RK (1944). Математическая теория оптики . Провиденс, Род-Айленд: Университет Брауна. С. 189–213.
2. Браун, Дж. (1953). Инженер беспроводной связи . 30 : 250. {{cite journal}}: Отсутствует или пусто |title=( помощь )
3. Гутман, А.С. (1954). «Модифицированная линза Люнеберга». J. Appl. Phys . 25 (7): 855–859. Bibcode : 1954JAP....25..855G. doi : 10.1063/1.1721757.
4. Морган, СП (1958). «Общее решение проблемы линзы Люнебурга». J. Appl. Phys . 29 (9): 1358–1368. Bibcode :1958JAP....29.1358M. doi :10.1063/1.1723441. S2CID  119949981.
5. "Решения задач (проб. 3, т. VIII. стр. 188)". Кембриджский и Дублинский математический журнал . 9. Macmillan: 9–11. 1854.
6. Badri, S Hadi и Gilarlue, MM (2019). «Рыбий глаз Максвелла как эффективный силовой соединитель между разнородными фотонно-кристаллическими волноводами». Optik . 185. Elsevier: 566–570. arXiv : 1904.01242 . Bibcode : 2019Optik.185..566B. doi : 10.1016/j.ijleo.2019.03.163. S2CID  91184610.{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
7. "Проблемы (3)". Кембриджский и Дублинский математический журнал . 8. Macmillan: 188. 1853.
8. Нивен, ред. (1890). Научные труды Джеймса Клерка Максвелла. Нью-Йорк: Dover Publications. стр. 76.
9. «Взгляд через линзу Люнебурга». www.eahison.com . 2019-08-08. Архивировано из оригинала 2021-09-27 . Получено 2021-04-05 .
10. Локки, Алекс (5 мая 2017 г.). «Эта странная модификация F-35 убивает его скрытность вблизи российской обороны — и на то есть веская причина». Business Insider . Архивировано из оригинала 25 декабря 2023 г.
11. Ло, YT ; Ли, SW (1993). Справочник по антеннам: Теория антенн. Springer. стр. 40. ISBN 9780442015930.

Внешние ссылки

• Анимация распространения через линзу Люнеберга (диэлектрическую антенну) с YouTube
• Анимация объектива Максвелла «Рыбий глаз» с YouTube
• Анимация полулинзы Максвелла «Рыбий глаз» (диэлектрическая антенна) с YouTube