Конститутивная модель идеально упругого материала.
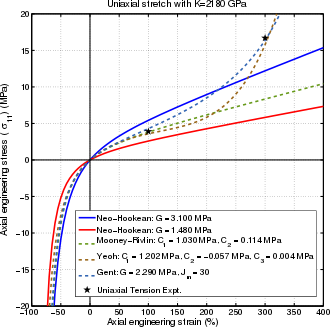
Кривые растяжения-деформации для различных моделей гиперупругих материалов. Гиперупругий или упругий материал Грина [1] представляет собой тип конститутивной модели идеально упругого материала, для которого зависимость напряжения от деформации выводится из функции плотности энергии деформации . Гиперупругий материал является частным случаем упругого материала Коши .
Для многих материалов линейно-упругие модели неточно описывают наблюдаемое поведение материала. Наиболее распространенным примером такого материала является резина, соотношение напряжения и деформации которой можно определить как нелинейно-упругое, изотропное и несжимаемое . Гиперупругость обеспечивает средство моделирования поведения таких материалов при напряжении и деформации. [2] Поведение ненаполненных вулканизированных эластомеров часто близко соответствует идеалу гиперэластичности. Наполненные эластомеры и биологические ткани [3] [4] также часто моделируются с помощью гиперэластичной идеализации.
Рональд Ривлин и Мелвин Муни разработали первые гиперупругие модели — твердые тела Нео-Хука и Муни-Ривлина . С тех пор было разработано множество других гиперэластичных моделей. Другие широко используемые модели гиперупругих материалов включают модель Огдена и модель Арруды-Бойса .
Модели гиперупругих материалов Модель Сен-Венана – Кирхгофа Простейшей моделью гиперупругого материала является модель Сен-Венана-Кирхгофа, которая представляет собой расширение геометрически линейной модели упругого материала до геометрически нелинейного режима. Эта модель имеет общий вид и изотропную форму соответственно.
S = C : E S = λ tr ( E ) I + 2 μ E . {\displaystyle {\begin{aligned}{\boldsymbol {S}}&={\boldsymbol {C}}:{\boldsymbol {E}}\\{\boldsymbol {S}}&=\lambda ~{\text{tr}}({\boldsymbol {E}}){\boldsymbol {\mathit {I}}}+2\mu {\boldsymbol {E}}{\text{.}}\end{aligned}}} тензор жесткости : {\displaystyle \mathbin {:} } S {\displaystyle {\boldsymbol {S}}} C : R 3 × 3 → R 3 × 3 {\displaystyle {\boldsymbol {C}}:\mathbb {R} ^{3\times 3}\to \mathbb {R} ^{3\times 3}} E {\displaystyle {\boldsymbol {E}}} E = 1 2 [ ( ∇ X u ) T + ∇ X u + ( ∇ X u ) T ⋅ ∇ X u ] {\displaystyle \mathbf {E} ={\frac {1}{2}}\left[(\nabla _{\mathbf {X} }\mathbf {u} )^{\textsf {T}}+\nabla _{\mathbf {X} }\mathbf {u} +(\nabla _{\mathbf {X} }\mathbf {u} )^{\textsf {T}}\cdot \nabla _{\mathbf {X} }\mathbf {u} \right]\,\!} λ {\displaystyle \lambda } константы Ламе μ {\displaystyle \mu } I {\displaystyle {\boldsymbol {\mathit {I}}}} Функция плотности энергии деформации для модели Сен-Венана – Кирхгофа равна
W ( E ) = λ 2 [ tr ( E ) ] 2 + μ tr ( E 2 ) {\displaystyle W({\boldsymbol {E}})={\frac {\lambda }{2}}[{\text{tr}}({\boldsymbol {E}})]^{2}+\mu {\text{tr}}{\mathord {\left({\boldsymbol {E}}^{2}\right)}}} а второе напряжение Пиолы–Кирхгофа можно получить из соотношения
S = ∂ W ∂ E . {\displaystyle {\boldsymbol {S}}={\frac {\partial W}{\partial {\boldsymbol {E}}}}~.} Классификация моделей гиперупругих материалов Модели гиперупругих материалов можно разделить на:
феноменологические описания наблюдаемого поведениямеханистические модели , вытекающие из аргументов об основной структуре материалагибриды феноменологических и механистических моделей Как правило, гиперэластичная модель должна удовлетворять критерию устойчивости Друкера . Некоторые гиперупругие модели удовлетворяют гипотезе Валаниса-Ландела, которая утверждает, что функцию энергии деформации можно разделить на сумму отдельных функций главных растяжений : ( λ 1 , λ 2 , λ 3 ) {\displaystyle (\lambda _{1},\lambda _{2},\lambda _{3})}
W = f ( λ 1 ) + f ( λ 2 ) + f ( λ 3 ) . {\displaystyle W=f(\lambda _{1})+f(\lambda _{2})+f(\lambda _{3})\,.} Отношения напряжение-деформация Сжимаемые гиперэластичные материалы Первое напряжение Пиолы – Кирхгофа Если – функция плотности энергии деформации, 1-й тензор напряжений Пиолы – Кирхгофа можно рассчитать для гиперупругого материала как W ( F ) {\displaystyle W({\boldsymbol {F}})}
P = ∂ W ∂ F or P i K = ∂ W ∂ F i K . {\displaystyle {\boldsymbol {P}}={\frac {\partial W}{\partial {\boldsymbol {F}}}}\qquad {\text{or}}\qquad P_{iK}={\frac {\partial W}{\partial F_{iK}}}.} деформации лагранжевой деформации Грина F {\displaystyle {\boldsymbol {F}}} E {\displaystyle {\boldsymbol {E}}} P = F ⋅ ∂ W ∂ E or P i K = F i L ∂ W ∂ E L K . {\displaystyle {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad P_{iK}=F_{iL}~{\frac {\partial W}{\partial E_{LK}}}~.} правого тензора деформации Коши–Грина C {\displaystyle {\boldsymbol {C}}} P = 2 F ⋅ ∂ W ∂ C or P i K = 2 F i L ∂ W ∂ C L K . {\displaystyle {\boldsymbol {P}}=2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\qquad {\text{or}}\qquad P_{iK}=2~F_{iL}~{\frac {\partial W}{\partial C_{LK}}}~.} Второе напряжение Пиолы – Кирхгофа Если – второй тензор напряжений Пиолы – Кирхгофа, то S {\displaystyle {\boldsymbol {S}}}
S = F − 1 ⋅ ∂ W ∂ F or S I J = F I k − 1 ∂ W ∂ F k J . {\displaystyle {\boldsymbol {S}}={\boldsymbol {F}}^{-1}\cdot {\frac {\partial W}{\partial {\boldsymbol {F}}}}\qquad {\text{or}}\qquad S_{IJ}=F_{Ik}^{-1}{\frac {\partial W}{\partial F_{kJ}}}~.} лагранжевой деформации Грина S = ∂ W ∂ E or S I J = ∂ W ∂ E I J . {\displaystyle {\boldsymbol {S}}={\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad S_{IJ}={\frac {\partial W}{\partial E_{IJ}}}~.} правого тензора деформации Коши–Грина S = 2 ∂ W ∂ C or S I J = 2 ∂ W ∂ C I J . {\displaystyle {\boldsymbol {S}}=2~{\frac {\partial W}{\partial {\boldsymbol {C}}}}\qquad {\text{or}}\qquad S_{IJ}=2~{\frac {\partial W}{\partial C_{IJ}}}~.} формула Дойла-Эриксена Коши стресс Аналогично, напряжение Коши определяется выражением
σ = 1 J ∂ W ∂ F ⋅ F T ; J := det F or σ i j = 1 J ∂ W ∂ F i K F j K . {\displaystyle {\boldsymbol {\sigma }}={\frac {1}{J}}~{\frac {\partial W}{\partial {\boldsymbol {F}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}~;~~J:=\det {\boldsymbol {F}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {1}{J}}~{\frac {\partial W}{\partial F_{iK}}}~F_{jK}~.} лагранжевой деформации Грина σ = 1 J F ⋅ ∂ W ∂ E ⋅ F T or σ i j = 1 J F i K ∂ W ∂ E K L F j L . {\displaystyle {\boldsymbol {\sigma }}={\frac {1}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {1}{J}}~F_{iK}~{\frac {\partial W}{\partial E_{KL}}}~F_{jL}~.} правого тензора деформации Коши–Грина σ = 2 J F ⋅ ∂ W ∂ C ⋅ F T or σ i j = 2 J F i K ∂ W ∂ C K L F j L . {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {2}{J}}~F_{iK}~{\frac {\partial W}{\partial C_{KL}}}~F_{jL}~.} неявно левый [7] σ = 2 J ∂ W ∂ B ⋅ B or σ i j = 2 J B i k ∂ W ∂ B k j . {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}{\frac {\partial W}{\partial {\boldsymbol {B}}}}\cdot ~{\boldsymbol {B}}\qquad {\text{or}}\qquad \sigma _{ij}={\frac {2}{J}}~B_{ik}~{\frac {\partial W}{\partial B_{kj}}}~.} Несжимаемые гиперупругие материалы Для несжимаемого материала . Следовательно, ограничение несжимаемости равно . Для обеспечения несжимаемости гиперупругого материала функцию энергии деформации можно записать в виде: J := det F = 1 {\displaystyle J:=\det {\boldsymbol {F}}=1} J − 1 = 0 {\displaystyle J-1=0}
W = W ( F ) − p ( J − 1 ) {\displaystyle W=W({\boldsymbol {F}})-p~(J-1)} множитель Лагранжа p {\displaystyle p} P = − p J F − T + ∂ W ∂ F = − p F − T + F ⋅ ∂ W ∂ E = − p F − T + 2 F ⋅ ∂ W ∂ C . {\displaystyle {\boldsymbol {P}}=-p~J{\boldsymbol {F}}^{-{\textsf {T}}}+{\frac {\partial W}{\partial {\boldsymbol {F}}}}=-p~{\boldsymbol {F}}^{-{\textsf {T}}}+{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}=-p~{\boldsymbol {F}}^{-{\textsf {T}}}+2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}~.} преобразовать тензор напряжений Коши σ = P ⋅ F T = − p 1 + ∂ W ∂ F ⋅ F T = − p 1 + F ⋅ ∂ W ∂ E ⋅ F T = − p 1 + 2 F ⋅ ∂ W ∂ C ⋅ F T . {\displaystyle {\boldsymbol {\sigma }}={\boldsymbol {P}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial {\boldsymbol {F}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}~.} Выражения для напряжения Коши Сжимаемые изотропные гиперупругие материалы Для изотропных гиперупругих материалов напряжение Коши можно выразить через инварианты левого тензора деформации Коши – Грина (или правого тензора деформации Коши – Грина ). Если функция плотности энергии деформации равна
W ( F ) = W ^ ( I 1 , I 2 , I 3 ) = W ¯ ( I ¯ 1 , I ¯ 2 , J ) = W ~ ( λ 1 , λ 2 , λ 3 ) , {\displaystyle W({\boldsymbol {F}})={\hat {W}}(I_{1},I_{2},I_{3})={\bar {W}}({\bar {I}}_{1},{\bar {I}}_{2},J)={\tilde {W}}(\lambda _{1},\lambda _{2},\lambda _{3}),} σ = 2 I 3 [ ( ∂ W ^ ∂ I 1 + I 1 ∂ W ^ ∂ I 2 ) B − ∂ W ^ ∂ I 2 B ⋅ B ] + 2 I 3 ∂ W ^ ∂ I 3 1 = 2 J [ 1 J 2 / 3 ( ∂ W ¯ ∂ I ¯ 1 + I ¯ 1 ∂ W ¯ ∂ I ¯ 2 ) B − 1 J 4 / 3 ∂ W ¯ ∂ I ¯ 2 B ⋅ B ] + [ ∂ W ¯ ∂ J − 2 3 J ( I ¯ 1 ∂ W ¯ ∂ I ¯ 1 + 2 I ¯ 2 ∂ W ¯ ∂ I ¯ 2 ) ] 1 = 2 J [ ( ∂ W ¯ ∂ I ¯ 1 + I ¯ 1 ∂ W ¯ ∂ I ¯ 2 ) B ¯ − ∂ W ¯ ∂ I ¯ 2 B ¯ ⋅ B ¯ ] + [ ∂ W ¯ ∂ J − 2 3 J ( I ¯ 1 ∂ W ¯ ∂ I ¯ 1 + 2 I ¯ 2 ∂ W ¯ ∂ I ¯ 2 ) ] 1 = λ 1 λ 1 λ 2 λ 3 ∂ W ~ ∂ λ 1 n 1 ⊗ n 1 + λ 2 λ 1 λ 2 λ 3 ∂ W ~ ∂ λ 2 n 2 ⊗ n 2 + λ 3 λ 1 λ 2 λ 3 ∂ W ~ ∂ λ 3 n 3 ⊗ n 3 {\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{\sqrt {I_{3}}}}\left[\left({\frac {\partial {\hat {W}}}{\partial I_{1}}}+I_{1}~{\frac {\partial {\hat {W}}}{\partial I_{2}}}\right){\boldsymbol {B}}-{\frac {\partial {\hat {W}}}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2{\sqrt {I_{3}}}~{\frac {\partial {\hat {W}}}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}\\[5pt]&={\frac {2}{J}}\left[{\frac {1}{J^{2/3}}}\left({\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}\right){\boldsymbol {B}}-{\frac {1}{J^{4/3}}}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\left[{\frac {\partial {\bar {W}}}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}\right)\right]~{\boldsymbol {\mathit {1}}}\\[5pt]&={\frac {2}{J}}\left[\left({\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}\right){\bar {\boldsymbol {B}}}-{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]+\left[{\frac {\partial {\bar {W}}}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}\right)\right]~{\boldsymbol {\mathit {1}}}\\[5pt]&={\frac {\lambda _{1}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac {\lambda _{2}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\frac {\lambda _{3}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}} левого тензора деформации Коши – Грина ). Доказательство 1 Второй тензор напряжений Пиолы – Кирхгофа для гиперупругого материала имеет вид
S = 2 ∂ W ∂ C {\displaystyle {\boldsymbol {S}}=2~{\frac {\partial W}{\partial {\boldsymbol {C}}}}} где –
правый тензор деформации Коши–Грина , –
градиент деформации . Напряжение Коши определяется выражением
C = F T ⋅ F {\displaystyle {\boldsymbol {C}}={\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}} F {\displaystyle {\boldsymbol {F}}} σ = 1 J F ⋅ S ⋅ F T = 2 J F ⋅ ∂ W ∂ C ⋅ F T {\displaystyle {\boldsymbol {\sigma }}={\frac {1}{J}}~{\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}={\frac {2}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{T}} где . Пусть – три главных инварианта . Затем
J = det F {\displaystyle J=\det {\boldsymbol {F}}} I 1 , I 2 , I 3 {\displaystyle I_{1},I_{2},I_{3}} C {\displaystyle {\boldsymbol {C}}} ∂ W ∂ C = ∂ W ∂ I 1 ∂ I 1 ∂ C + ∂ W ∂ I 2 ∂ I 2 ∂ C + ∂ W ∂ I 3 ∂ I 3 ∂ C . {\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial I_{2}}}~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial I_{3}}}~{\frac {\partial I_{3}}{\partial {\boldsymbol {C}}}}~.} Производные
инвариантов симметричного тензора имеют вид
C {\displaystyle {\boldsymbol {C}}} ∂ I 1 ∂ C = 1 ; ∂ I 2 ∂ C = I 1 1 − C ; ∂ I 3 ∂ C = det ( C ) C − 1 {\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}={\boldsymbol {\mathit {1}}}~;~~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {C}}~;~~{\frac {\partial I_{3}}{\partial {\boldsymbol {C}}}}=\det({\boldsymbol {C}})~{\boldsymbol {C}}^{-1}} Поэтому мы можем написать
∂ W ∂ C = ∂ W ∂ I 1 1 + ∂ W ∂ I 2 ( I 1 1 − F T ⋅ F ) + ∂ W ∂ I 3 I 3 F − 1 ⋅ F − T . {\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}})+{\frac {\partial W}{\partial I_{3}}}~I_{3}~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {F}}^{-T}~.} Подстановка выражения для напряжения Коши дает
σ = 2 J [ ∂ W ∂ I 1 F ⋅ F T + ∂ W ∂ I 2 ( I 1 F ⋅ F T − F ⋅ F T ⋅ F ⋅ F T ) + ∂ W ∂ I 3 I 3 1 ] {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~\left[{\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}+{\frac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}-{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T})+{\frac {\partial W}{\partial I_{3}}}~I_{3}~{\boldsymbol {\mathit {1}}}\right]} Используя
левый тензор деформации Коши–Грина и учитывая, что , можем записать
B = F ⋅ F T {\displaystyle {\boldsymbol {B}}={\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}} I 3 = J 2 {\displaystyle I_{3}=J^{2}} σ = 2 I 3 [ ( ∂ W ∂ I 1 + I 1 ∂ W ∂ I 2 ) B − ∂ W ∂ I 2 B ⋅ B ] + 2 I 3 ∂ W ∂ I 3 1 . {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{\sqrt {I_{3}}}}~\left[\left({\frac {\partial W}{\partial I_{1}}}+I_{1}~{\frac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~{\sqrt {I_{3}}}~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.} Для
несжимаемого материала и, следовательно , .Тогда
I 3 = 1 {\displaystyle I_{3}=1} W = W ( I 1 , I 2 ) {\displaystyle W=W(I_{1},I_{2})} ∂ W ∂ C = ∂ W ∂ I 1 ∂ I 1 ∂ C + ∂ W ∂ I 2 ∂ I 2 ∂ C = ∂ W ∂ I 1 1 + ∂ W ∂ I 2 ( I 1 1 − F T ⋅ F ) {\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial I_{2}}}~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}})} Следовательно, напряжение Коши определяется выражением
σ = 2 [ ( ∂ W ∂ I 1 + I 1 ∂ W ∂ I 2 ) B − ∂ W ∂ I 2 B ⋅ B ] − p 1 . {\displaystyle {\boldsymbol {\sigma }}=2\left[\left({\frac {\partial W}{\partial I_{1}}}+I_{1}~{\frac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]-p~{\boldsymbol {\mathit {1}}}~.} где – неопределенное давление, которое действует как
множитель Лагранжа , обеспечивая соблюдение ограничения несжимаемости.
p {\displaystyle p} Если, кроме того, имеем и, следовательно, I 1 = I 2 {\displaystyle I_{1}=I_{2}} W = W ( I 1 ) {\displaystyle W=W(I_{1})}
∂ W ∂ C = ∂ W ∂ I 1 ∂ I 1 ∂ C = ∂ W ∂ I 1 1 {\displaystyle {\frac {\partial W}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}={\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}} В этом случае напряжение Коши можно выразить как
σ = 2 ∂ W ∂ I 1 B − p 1 . {\displaystyle {\boldsymbol {\sigma }}=2{\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}-p~{\boldsymbol {\mathit {1}}}~.} Доказательство 2 Градиент изохорной деформации определяется как , в результате чего градиент изохорной деформации имеет определитель, равный 1, другими словами, он не имеет объемного растяжения. Используя это, можно впоследствии определить изохорный левый тензор деформации Коши – Грина . Инварианты _ F ¯ := J − 1 / 3 F {\displaystyle {\bar {\boldsymbol {F}}}:=J^{-1/3}{\boldsymbol {F}}} B ¯ := F ¯ ⋅ F ¯ T = J − 2 / 3 B {\displaystyle {\bar {\boldsymbol {B}}}:={\bar {\boldsymbol {F}}}\cdot {\bar {\boldsymbol {F}}}^{T}=J^{-2/3}{\boldsymbol {B}}} B ¯ {\displaystyle {\bar {\boldsymbol {B}}}}
I ¯ 1 = tr ( B ¯ ) = J − 2 / 3 tr ( B ) = J − 2 / 3 I 1 I ¯ 2 = 1 2 ( tr ( B ¯ ) 2 − tr ( B ¯ 2 ) ) = 1 2 ( ( J − 2 / 3 tr ( B ) ) 2 − tr ( J − 4 / 3 B 2 ) ) = J − 4 / 3 I 2 I ¯ 3 = det ( B ¯ ) = J − 6 / 3 det ( B ) = J − 2 I 3 = J − 2 J 2 = 1 {\displaystyle {\begin{aligned}{\bar {I}}_{1}&={\text{tr}}({\bar {\boldsymbol {B}}})=J^{-2/3}{\text{tr}}({\boldsymbol {B}})=J^{-2/3}I_{1}\\{\bar {I}}_{2}&={\frac {1}{2}}\left({\text{tr}}({\bar {\boldsymbol {B}}})^{2}-{\text{tr}}({\bar {\boldsymbol {B}}}^{2})\right)={\frac {1}{2}}\left(\left(J^{-2/3}{\text{tr}}({\boldsymbol {B}})\right)^{2}-{\text{tr}}(J^{-4/3}{\boldsymbol {B}}^{2})\right)=J^{-4/3}I_{2}\\{\bar {I}}_{3}&=\det({\bar {\boldsymbol {B}}})=J^{-6/3}\det({\boldsymbol {B}})=J^{-2}I_{3}=J^{-2}J^{2}=1\end{aligned}}} Набор инвариантов, которые используются для определения искажающего поведения, представляют собой первые два инварианта изохорного левого тензора тензора деформации Коши – Грина (которые идентичны инвариантам для правого тензора растяжения Коши Грина) и добавляются к описать объемное поведение.
J {\displaystyle J} Чтобы выразить напряжение Коши через инварианты, напомним, что I ¯ 1 , I ¯ 2 , J {\displaystyle {\bar {I}}_{1},{\bar {I}}_{2},J}
I ¯ 1 = J − 2 / 3 I 1 = I 3 − 1 / 3 I 1 ; I ¯ 2 = J − 4 / 3 I 2 = I 3 − 2 / 3 I 2 ; J = I 3 1 / 2 . {\displaystyle {\bar {I}}_{1}=J^{-2/3}~I_{1}=I_{3}^{-1/3}~I_{1}~;~~{\bar {I}}_{2}=J^{-4/3}~I_{2}=I_{3}^{-2/3}~I_{2}~;~~J=I_{3}^{1/2}~.} Цепное правило дифференциации дает нам
∂ W ∂ I 1 = ∂ W ∂ I ¯ 1 ∂ I ¯ 1 ∂ I 1 + ∂ W ∂ I ¯ 2 ∂ I ¯ 2 ∂ I 1 + ∂ W ∂ J ∂ J ∂ I 1 = I 3 − 1 / 3 ∂ W ∂ I ¯ 1 = J − 2 / 3 ∂ W ∂ I ¯ 1 ∂ W ∂ I 2 = ∂ W ∂ I ¯ 1 ∂ I ¯ 1 ∂ I 2 + ∂ W ∂ I ¯ 2 ∂ I ¯ 2 ∂ I 2 + ∂ W ∂ J ∂ J ∂ I 2 = I 3 − 2 / 3 ∂ W ∂ I ¯ 2 = J − 4 / 3 ∂ W ∂ I ¯ 2 ∂ W ∂ I 3 = ∂ W ∂ I ¯ 1 ∂ I ¯ 1 ∂ I 3 + ∂ W ∂ I ¯ 2 ∂ I ¯ 2 ∂ I 3 + ∂ W ∂ J ∂ J ∂ I 3 = − 1 3 I 3 − 4 / 3 I 1 ∂ W ∂ I ¯ 1 − 2 3 I 3 − 5 / 3 I 2 ∂ W ∂ I ¯ 2 + 1 2 I 3 − 1 / 2 ∂ W ∂ J = − 1 3 J − 8 / 3 J 2 / 3 I ¯ 1 ∂ W ∂ I ¯ 1 − 2 3 J − 10 / 3 J 4 / 3 I ¯ 2 ∂ W ∂ I ¯ 2 + 1 2 J − 1 ∂ W ∂ J = − 1 3 J − 2 ( I ¯ 1 ∂ W ∂ I ¯ 1 + 2 I ¯ 2 ∂ W ∂ I ¯ 2 ) + 1 2 J − 1 ∂ W ∂ J {\displaystyle {\begin{aligned}{\frac {\partial W}{\partial I_{1}}}&={\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\frac {\partial {\bar {I}}_{1}}{\partial I_{1}}}+{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\frac {\partial {\bar {I}}_{2}}{\partial I_{1}}}+{\frac {\partial W}{\partial J}}~{\frac {\partial J}{\partial I_{1}}}\\&=I_{3}^{-1/3}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}=J^{-2/3}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}\\{\frac {\partial W}{\partial I_{2}}}&={\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\frac {\partial {\bar {I}}_{1}}{\partial I_{2}}}+{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\frac {\partial {\bar {I}}_{2}}{\partial I_{2}}}+{\frac {\partial W}{\partial J}}~{\frac {\partial J}{\partial I_{2}}}\\&=I_{3}^{-2/3}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}=J^{-4/3}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\\{\frac {\partial W}{\partial I_{3}}}&={\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\frac {\partial {\bar {I}}_{1}}{\partial I_{3}}}+{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\frac {\partial {\bar {I}}_{2}}{\partial I_{3}}}+{\frac {\partial W}{\partial J}}~{\frac {\partial J}{\partial I_{3}}}\\&=-{\frac {1}{3}}~I_{3}^{-4/3}~I_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}-{\frac {2}{3}}~I_{3}^{-5/3}~I_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}+{\frac {1}{2}}~I_{3}^{-1/2}~{\frac {\partial W}{\partial J}}\\&=-{\frac {1}{3}}~J^{-8/3}~J^{2/3}~{\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}-{\frac {2}{3}}~J^{-10/3}~J^{4/3}~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}+{\frac {1}{2}}~J^{-1}~{\frac {\partial W}{\partial J}}\\&=-{\frac {1}{3}}~J^{-2}~\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)+{\frac {1}{2}}~J^{-1}~{\frac {\partial W}{\partial J}}\end{aligned}}} Напомним, что напряжение Коши определяется выражением
σ = 2 I 3 [ ( ∂ W ∂ I 1 + I 1 ∂ W ∂ I 2 ) B − ∂ W ∂ I 2 B ⋅ B ] + 2 I 3 ∂ W ∂ I 3 1 . {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{\sqrt {I_{3}}}}~\left[\left({\frac {\partial W}{\partial I_{1}}}+I_{1}~{\frac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~{\sqrt {I_{3}}}~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.} В терминах инвариантов мы имеем
I ¯ 1 , I ¯ 2 , J {\displaystyle {\bar {I}}_{1},{\bar {I}}_{2},J} σ = 2 J [ ( ∂ W ∂ I 1 + J 2 / 3 I ¯ 1 ∂ W ∂ I 2 ) B − ∂ W ∂ I 2 B ⋅ B ] + 2 J ∂ W ∂ I 3 1 . {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~\left[\left({\frac {\partial W}{\partial I_{1}}}+J^{2/3}~{\bar {I}}_{1}~{\frac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~J~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.} Подставив выражения для производных через , получим
W {\displaystyle W} I ¯ 1 , I ¯ 2 , J {\displaystyle {\bar {I}}_{1},{\bar {I}}_{2},J} σ = 2 J [ ( J − 2 / 3 ∂ W ∂ I ¯ 1 + J − 2 / 3 I ¯ 1 ∂ W ∂ I ¯ 2 ) B − J − 4 / 3 ∂ W ∂ I ¯ 2 B ⋅ B ] + 2 J [ − 1 3 J − 2 ( I ¯ 1 ∂ W ∂ I ¯ 1 + 2 I ¯ 2 ∂ W ∂ I ¯ 2 ) + 1 2 J − 1 ∂ W ∂ J ] 1 {\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left[\left(J^{-2/3}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+J^{-2/3}~{\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\boldsymbol {B}}-J^{-4/3}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\\&\qquad 2~J~\left[-{\frac {1}{3}}~J^{-2}~\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)+{\frac {1}{2}}~J^{-1}~{\frac {\partial W}{\partial J}}\right]~{\boldsymbol {\mathit {1}}}\end{aligned}}} или,
σ = 2 J [ 1 J 2 / 3 ( ∂ W ∂ I ¯ 1 + I ¯ 1 ∂ W ∂ I ¯ 2 ) B − 1 J 4 / 3 ∂ W ∂ I ¯ 2 B ⋅ B ] + [ ∂ W ∂ J − 2 3 J ( I ¯ 1 ∂ W ∂ I ¯ 1 + 2 I ¯ 2 ∂ W ∂ I ¯ 2 ) ] 1 {\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left[{\frac {1}{J^{2/3}}}~\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\boldsymbol {B}}-{\frac {1}{J^{4/3}}}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]\\&\qquad +\left[{\frac {\partial W}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)\right]{\boldsymbol {\mathit {1}}}\end{aligned}}} В терминах девиаторной части можно написать
B {\displaystyle {\boldsymbol {B}}} σ = 2 J [ ( ∂ W ∂ I ¯ 1 + I ¯ 1 ∂ W ∂ I ¯ 2 ) B ¯ − ∂ W ∂ I ¯ 2 B ¯ ⋅ B ¯ ] + [ ∂ W ∂ J − 2 3 J ( I ¯ 1 ∂ W ∂ I ¯ 1 + 2 I ¯ 2 ∂ W ∂ I ¯ 2 ) ] 1 {\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left[\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]\\&\qquad +\left[{\frac {\partial W}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)\right]{\boldsymbol {\mathit {1}}}\end{aligned}}} Для
несжимаемого материала и, следовательно , . Тогда напряжение Коши определяется выражением
J = 1 {\displaystyle J=1} W = W ( I ¯ 1 , I ¯ 2 ) {\displaystyle W=W({\bar {I}}_{1},{\bar {I}}_{2})} σ = 2 [ ( ∂ W ∂ I ¯ 1 + I 1 ∂ W ∂ I ¯ 2 ) B ¯ − ∂ W ∂ I ¯ 2 B ¯ ⋅ B ¯ ] − p 1 . {\displaystyle {\boldsymbol {\sigma }}=2\left[\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+I_{1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]-p~{\boldsymbol {\mathit {1}}}~.} где – неопределенный член множителя Лагранжа, подобный давлению. Кроме того, если , мы имеем и, следовательно, напряжение Коши можно выразить как
p {\displaystyle p} I ¯ 1 = I ¯ 2 {\displaystyle {\bar {I}}_{1}={\bar {I}}_{2}} W = W ( I ¯ 1 ) {\displaystyle W=W({\bar {I}}_{1})} σ = 2 ∂ W ∂ I ¯ 1 B ¯ − p 1 . {\displaystyle {\boldsymbol {\sigma }}=2{\frac {\partial W}{\partial {\bar {I}}_{1}}}~{\bar {\boldsymbol {B}}}-p~{\boldsymbol {\mathit {1}}}~.} Доказательство 3 Чтобы выразить напряжение Коши через растяжения, напомним , что λ 1 , λ 2 , λ 3 {\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}
∂ λ i ∂ C = 1 2 λ i R T ⋅ ( n i ⊗ n i ) ⋅ R ; i = 1 , 2 , 3 . {\displaystyle {\frac {\partial \lambda _{i}}{\partial {\boldsymbol {C}}}}={\frac {1}{2\lambda _{i}}}~{\boldsymbol {R}}^{T}\cdot (\mathbf {n} _{i}\otimes \mathbf {n} _{i})\cdot {\boldsymbol {R}}~;~~i=1,2,3~.} Цепное правило дает
∂ W ∂ C = ∂ W ∂ λ 1 ∂ λ 1 ∂ C + ∂ W ∂ λ 2 ∂ λ 2 ∂ C + ∂ W ∂ λ 3 ∂ λ 3 ∂ C = R T ⋅ [ 1 2 λ 1 ∂ W ∂ λ 1 n 1 ⊗ n 1 + 1 2 λ 2 ∂ W ∂ λ 2 n 2 ⊗ n 2 + 1 2 λ 3 ∂ W ∂ λ 3 n 3 ⊗ n 3 ] ⋅ R {\displaystyle {\begin{aligned}{\frac {\partial W}{\partial {\boldsymbol {C}}}}&={\frac {\partial W}{\partial \lambda _{1}}}~{\frac {\partial \lambda _{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial \lambda _{2}}}~{\frac {\partial \lambda _{2}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial \lambda _{3}}}~{\frac {\partial \lambda _{3}}{\partial {\boldsymbol {C}}}}\\&={\boldsymbol {R}}^{T}\cdot \left[{\frac {1}{2\lambda _{1}}}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac {1}{2\lambda _{2}}}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\frac {1}{2\lambda _{3}}}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\right]\cdot {\boldsymbol {R}}\end{aligned}}} Напряжение Коши определяется выражением
σ = 2 J F ⋅ ∂ W ∂ C ⋅ F T = 2 J ( V ⋅ R ) ⋅ ∂ W ∂ C ⋅ ( R T ⋅ V ) {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{T}={\frac {2}{J}}~({\boldsymbol {V}}\cdot {\boldsymbol {R}})\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\cdot ({\boldsymbol {R}}^{T}\cdot {\boldsymbol {V}})} Подстановка выражения для производной приводит к
W {\displaystyle W} σ = 2 J V ⋅ [ 1 2 λ 1 ∂ W ∂ λ 1 n 1 ⊗ n 1 + 1 2 λ 2 ∂ W ∂ λ 2 n 2 ⊗ n 2 + 1 2 λ 3 ∂ W ∂ λ 3 n 3 ⊗ n 3 ] ⋅ V {\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {V}}\cdot \left[{\frac {1}{2\lambda _{1}}}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac {1}{2\lambda _{2}}}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\frac {1}{2\lambda _{3}}}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\right]\cdot {\boldsymbol {V}}} Используя
спектральное разложение, мы имеем
V {\displaystyle {\boldsymbol {V}}} V ⋅ ( n i ⊗ n i ) ⋅ V = λ i 2 n i ⊗ n i ; i = 1 , 2 , 3. {\displaystyle {\boldsymbol {V}}\cdot (\mathbf {n} _{i}\otimes \mathbf {n} _{i})\cdot {\boldsymbol {V}}=\lambda _{i}^{2}~\mathbf {n} _{i}\otimes \mathbf {n} _{i}~;~~i=1,2,3.} Также обратите внимание, что
J = det ( F ) = det ( V ) det ( R ) = det ( V ) = λ 1 λ 2 λ 3 . {\displaystyle J=\det({\boldsymbol {F}})=\det({\boldsymbol {V}})\det({\boldsymbol {R}})=\det({\boldsymbol {V}})=\lambda _{1}\lambda _{2}\lambda _{3}~.} Следовательно, выражение для напряжения Коши можно записать как
σ = 1 λ 1 λ 2 λ 3 [ λ 1 ∂ W ∂ λ 1 n 1 ⊗ n 1 + λ 2 ∂ W ∂ λ 2 n 2 ⊗ n 2 + λ 3 ∂ W ∂ λ 3 n 3 ⊗ n 3 ] {\displaystyle {\boldsymbol {\sigma }}={\frac {1}{\lambda _{1}\lambda _{2}\lambda _{3}}}~\left[\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\right]} Для
несжимаемого материала и, следовательно , . Следуя Огдену
[1], с. 485, мы можем написать
λ 1 λ 2 λ 3 = 1 {\displaystyle \lambda _{1}\lambda _{2}\lambda _{3}=1} W = W ( λ 1 , λ 2 ) {\displaystyle W=W(\lambda _{1},\lambda _{2})} σ = λ 1 ∂ W ∂ λ 1 n 1 ⊗ n 1 + λ 2 ∂ W ∂ λ 2 n 2 ⊗ n 2 + λ 3 ∂ W ∂ λ 3 n 3 ⊗ n 3 − p 1 {\displaystyle {\boldsymbol {\sigma }}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}-p~{\boldsymbol {\mathit {1}}}~} На этом этапе требуется некоторая осторожность, поскольку, когда собственное значение повторяется, оно, как правило,
дифференцируемо только по Гато , но не
дифференцируемо по Фреше .
[8] [9] Строгую
тензорную производную можно найти только путем решения другой проблемы собственных значений.
Если выразить напряжение через различия между компонентами,
σ 11 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 ; σ 22 − σ 33 = λ 2 ∂ W ∂ λ 2 − λ 3 ∂ W ∂ λ 3 {\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}} Если помимо несжимаемости мы имеем, то для возможного решения задачи требуется и разность напряжений можно записать в виде
λ 1 = λ 2 {\displaystyle \lambda _{1}=\lambda _{2}} σ 11 = σ 22 {\displaystyle \sigma _{11}=\sigma _{22}} σ 11 − σ 33 = σ 22 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 {\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}} Несжимаемые изотропные гиперупругие материалы Для несжимаемых изотропных гиперупругих материалов функция плотности энергии деформации равна . Тогда напряжение Коши определяется выражением W ( F ) = W ^ ( I 1 , I 2 ) {\displaystyle W({\boldsymbol {F}})={\hat {W}}(I_{1},I_{2})}
σ = − p 1 + 2 [ ( ∂ W ^ ∂ I 1 + I 1 ∂ W ^ ∂ I 2 ) B − ∂ W ^ ∂ I 2 B ⋅ B ] = − p 1 + 2 [ ( ∂ W ∂ I ¯ 1 + I 1 ∂ W ∂ I ¯ 2 ) B ¯ − ∂ W ∂ I ¯ 2 B ¯ ⋅ B ¯ ] = − p 1 + λ 1 ∂ W ∂ λ 1 n 1 ⊗ n 1 + λ 2 ∂ W ∂ λ 2 n 2 ⊗ n 2 + λ 3 ∂ W ∂ λ 3 n 3 ⊗ n 3 {\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&=-p~{\boldsymbol {\mathit {1}}}+2\left[\left({\frac {\partial {\hat {W}}}{\partial I_{1}}}+I_{1}~{\frac {\partial {\hat {W}}}{\partial I_{2}}}\right){\boldsymbol {B}}-{\frac {\partial {\hat {W}}}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]\\&=-p~{\boldsymbol {\mathit {1}}}+2\left[\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+I_{1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]\\&=-p~{\boldsymbol {\mathit {1}}}+\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}} p {\displaystyle p} σ 11 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 ; σ 22 − σ 33 = λ 2 ∂ W ∂ λ 2 − λ 3 ∂ W ∂ λ 3 {\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}} I 1 = I 2 {\displaystyle I_{1}=I_{2}} σ = 2 ∂ W ∂ I 1 B − p 1 . {\displaystyle {\boldsymbol {\sigma }}=2{\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}-p~{\boldsymbol {\mathit {1}}}~.} λ 1 = λ 2 {\displaystyle \lambda _{1}=\lambda _{2}} σ 11 − σ 33 = σ 22 − σ 33 = λ 1 ∂ W ∂ λ 1 − λ 3 ∂ W ∂ λ 3 {\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}} Согласованность с линейной эластичностью Соответствие линейной упругости часто используется для определения некоторых параметров моделей гиперупругих материалов. Эти условия согласованности можно найти, сравнивая закон Гука с линеаризованной гиперупругостью при малых деформациях.
Условия совместности изотропных гиперупругих моделей Чтобы изотропные гиперупругие материалы соответствовали изотропной линейной упругости , соотношение напряжение-деформация должно иметь следующий вид в пределе бесконечно малой деформации :
σ = λ t r ( ε ) 1 + 2 μ ε {\displaystyle {\boldsymbol {\sigma }}=\lambda ~\mathrm {tr} ({\boldsymbol {\varepsilon }})~{\boldsymbol {\mathit {1}}}+2\mu {\boldsymbol {\varepsilon }}} константы [1] λ , μ {\displaystyle \lambda ,\mu } W = 1 2 λ [ t r ( ε ) ] 2 + μ t r ( ε 2 ) {\displaystyle W={\tfrac {1}{2}}\lambda ~[\mathrm {tr} ({\boldsymbol {\varepsilon }})]^{2}+\mu ~\mathrm {tr} {\mathord {\left({\boldsymbol {\varepsilon }}^{2}\right)}}} t r ( ε ) = 0 {\displaystyle \mathrm {tr} ({\boldsymbol {\varepsilon }})=0} W = μ t r ( ε 2 ) {\displaystyle W=\mu ~\mathrm {tr} {\mathord {\left({\boldsymbol {\varepsilon }}^{2}\right)}}} [1] W ( λ 1 , λ 2 , λ 3 ) {\displaystyle W(\lambda _{1},\lambda _{2},\lambda _{3})} W ( 1 , 1 , 1 ) = 0 ; ∂ W ∂ λ i ( 1 , 1 , 1 ) = 0 ∂ 2 W ∂ λ i ∂ λ j ( 1 , 1 , 1 ) = λ + 2 μ δ i j {\displaystyle {\begin{aligned}&W(1,1,1)=0~;~~{\frac {\partial W}{\partial \lambda _{i}}}(1,1,1)=0\\&{\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}(1,1,1)=\lambda +2\mu \delta _{ij}\end{aligned}}} Если материал несжимаем , то указанные выше условия можно выразить в следующем виде.
W ( 1 , 1 , 1 ) = 0 ∂ W ∂ λ i ( 1 , 1 , 1 ) = ∂ W ∂ λ j ( 1 , 1 , 1 ) ; ∂ 2 W ∂ λ i 2 ( 1 , 1 , 1 ) = ∂ 2 W ∂ λ j 2 ( 1 , 1 , 1 ) ∂ 2 W ∂ λ i ∂ λ j ( 1 , 1 , 1 ) = i n d e p e n d e n t o f i , j ≠ i ∂ 2 W ∂ λ i 2 ( 1 , 1 , 1 ) − ∂ 2 W ∂ λ i ∂ λ j ( 1 , 1 , 1 ) + ∂ W ∂ λ i ( 1 , 1 , 1 ) = 2 μ ( i ≠ j ) {\displaystyle {\begin{aligned}&W(1,1,1)=0\\&{\frac {\partial W}{\partial \lambda _{i}}}(1,1,1)={\frac {\partial W}{\partial \lambda _{j}}}(1,1,1)~;~~{\frac {\partial ^{2}W}{\partial \lambda _{i}^{2}}}(1,1,1)={\frac {\partial ^{2}W}{\partial \lambda _{j}^{2}}}(1,1,1)\\&{\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}(1,1,1)=\mathrm {independentof} ~i,j\neq i\\&{\frac {\partial ^{2}W}{\partial \lambda _{i}^{2}}}(1,1,1)-{\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}(1,1,1)+{\frac {\partial W}{\partial \lambda _{i}}}(1,1,1)=2\mu ~~(i\neq j)\end{aligned}}} Условия однородности несжимаемых резиновых материалов на основе I 1 Многие эластомеры адекватно моделируются функцией плотности энергии деформации, которая зависит только от . Для таких материалов у нас есть . Тогда условия согласованности несжимаемых материалов можно выразить как I 1 {\displaystyle I_{1}} W = W ( I 1 ) {\displaystyle W=W(I_{1})} I 1 = 3 , λ i = λ j = 1 {\displaystyle I_{1}=3,\lambda _{i}=\lambda _{j}=1}
W ( I 1 ) | I 1 = 3 = 0 and ∂ W ∂ I 1 | I 1 = 3 = μ 2 . {\displaystyle \left.W(I_{1})\right|_{I_{1}=3}=0\quad {\text{and}}\quad \left.{\frac {\partial W}{\partial I_{1}}}\right|_{I_{1}=3}={\frac {\mu }{2}}\,.} ∂ W ∂ λ i = ∂ W ∂ I 1 ∂ I 1 ∂ λ i = 2 λ i ∂ W ∂ I 1 and ∂ 2 W ∂ λ i ∂ λ j = 2 δ i j ∂ W ∂ I 1 + 4 λ i λ j ∂ 2 W ∂ I 1 2 . {\displaystyle {\frac {\partial W}{\partial \lambda _{i}}}={\frac {\partial W}{\partial I_{1}}}{\frac {\partial I_{1}}{\partial \lambda _{i}}}=2\lambda _{i}{\frac {\partial W}{\partial I_{1}}}\quad {\text{and}}\quad {\frac {\partial ^{2}W}{\partial \lambda _{i}\partial \lambda _{j}}}=2\delta _{ij}{\frac {\partial W}{\partial I_{1}}}+4\lambda _{i}\lambda _{j}{\frac {\partial ^{2}W}{\partial I_{1}^{2}}}\,.} Рекомендации ^ abcde RW Огден, 1984, Нелинейные упругие деформации , ISBN 0-486-69648-0 , Дувр. ^ Мюр, АХ (2005). «Моделирование деформационного поведения резины». Химия и технология резины . 78 (3): 391–425. дои : 10.5254/1.3547890. ^ Гао, Х; Макс; Ци, Н; Берри, К; Гриффит, Бельгия; Ло, X (2014). «Нелинейная модель митрального клапана человека с конечной деформацией и взаимодействием жидкости и структуры». Int J Numer Method Biomed Eng . 30 (12): 1597–613. дои : 10.1002/cnm.2691. ПМЦ 4278556 . ПМИД 25319496. ^ Цзя, Ф; Бен Амар, М; Биллоуд, Б; Чарриер, Б. (2017). «Морфоэластичность в развитии бурой водоросли Ectocarpus siliculosus: от округления клеток к ветвлению». Интерфейс JR Soc . 14 (127): 20160596. doi :10.1098/rsif.2016.0596. ПМЦ 5332559 . ПМИД 28228537. ^ Арруда, EM; Бойс, MC (1993). «Трехмерная модель поведения резиновых эластичных материалов при большом растяжении» (PDF) . Дж. Мех. Физ. Твердые тела . 41 : 389–412. дои : 10.1016/0022-5096(93)90013-6. S2CID 136924401. ^ Буч, MR; Зильберштейн, Миннесота (2020). «Статистическая механическая конститутивная теория полимерных сетей: неразрывные связи между распределением, поведением и ансамблем». Физ. Преподобный Е. 102 (1): 012501. arXiv : 2004.07874 . Бибкод : 2020PhRvE.102a2501B. doi : 10.1103/PhysRevE.102.012501. PMID 32794915. S2CID 215814600. ^ Ю. Басар, 2000, Нелинейная механика сплошной среды твердого тела, Springer, с. 157. ^ Фокс и Капур, Скорость изменения собственных значений и собственных векторов , Журнал AIAA , 6 (12) 2426–2429 (1968) ^ Фрисвелл М.И. Производные повторяющихся собственных значений и связанных с ними собственных векторов. Журнал вибрации и акустики (ASME), 1996 г.; 118:390–397. Смотрите также
![{\displaystyle \mathbf {E} = {\frac {1}{2}}\left[(\nabla _ {\mathbf {X} }\mathbf {u})^{\textsf {T}}+\nabla _ {\mathbf {X} }\mathbf {u} +(\nabla _ {\mathbf {X} }\mathbf {u} )^{\textsf {T}}\cdot \nabla _{\mathbf {X} }\mathbf {u} \right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c8b59fed4fc1f45e08b5f6ae13fe5e5f2586951)
![{\displaystyle W({\boldsymbol {E}})={\frac {\lambda }{2}}[{\text{tr}}({\boldsymbol {E}})]^{2}+\mu {\text{tr}}{\mathord {\left({\boldsymbol {E}}^{2}\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de41de18a428e0920a40050db04bdf7653ef0c5f)
![{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{\sqrt {I_{3}}}}\left[\left({\frac {\partial {\ шляпа {W}}}{\partial I_{1}}}+I_{1}~{\frac {\partial {\hat {W}}}{\partial I_{2}}}\right){\boldsymbol {B}}-{\frac {\partial {\hat {W}}}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2 {\sqrt {I_{3}}}~{\frac {\partial {\hat {W}}}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}\\[5pt ]&={\frac {2}{J}}\left[{\frac {1}{J^{2/3}}}\left({\frac {\partial {\bar {W}}}{ \partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial {\bar {W}}}{\partial {\bar {I }}_{2}}}\right){\boldsymbol {B}}-{\frac {1}{J^{4/3}}}~{\frac {\partial {\bar {W}}} {\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\left[{\frac {\partial {\bar { W}}}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\frac {\partial {\bar {W}}} {\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial {\bar {W}}}{\partial {\ bar {I}}_{2}}}\right)\right]~{\boldsymbol {\mathit {1}}}\\[5pt]&={\frac {2}{J}}\left[\ left({\frac {\partial {\bar {W}}}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\ частичный {\bar {W}}}{\partial {\bar {I}}_{2}}}\right){\bar {\boldsymbol {B}}}-{\frac {\partial {\bar { W}}}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]+\ left[{\frac {\partial {\bar {W}}}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\ frac {\partial {\bar {W}}}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial { \bar {W}}}{\partial {\bar {I}}_{2}}}\right)\right]~{\boldsymbol {\mathit {1}}}\\[5pt]&={\ frac {\lambda _{1}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac {\lambda _{2}}{\lambda _{1}\lambda _{ 2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\frac {\lambda _{3}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\frac {\partial {\tilde {W}}}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc63e121bafc2f5ebc99e2cc102ff55e68618452)
![{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~\left[{\frac {\partial W}{\partial I_{1}}}~{\boldsymbol {F} }\cdot {\boldsymbol {F}}^{T}+{\frac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {F}}\cdot {\ boldsymbol {F}}^{T}-{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}\cdot {\boldsymbol {F}}^{ T})+{\frac {\partial W}{\partial I_{3}}}~I_{3}~{\boldsymbol {\mathit {1}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fceb8e2cf5d2f77071ed86209e41e3b391829c7)
![{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{\sqrt {I_{3}}}}~\left[\left({\frac {\partial W}{\partial I_{1 }}}+I_{1}~{\frac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac {\partial W}{\partial I_ {2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~{\sqrt {I_{3}}}~{\frac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5e6b445b86b2c353a1f18494fc0b3d6cee61325)
![{\displaystyle {\boldsymbol {\sigma }}=2\left[\left({\frac {\partial W}{\partial I_{1}}}+I_{1}~{\frac {\partial W} {\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\ полужирный символ {B}}\right]-p~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29f1bd839ed56c70acb2202948b7027a97467764)
![{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~\left[\left({\frac {\partial W}{\partial I_{1}}}+J^{ 2/3}~{\bar {I}}_{1}~{\frac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\frac { \partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~J~{\frac {\partial W}{\partial I_ {3}}}~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4976e9a59607a67563a2168f67cac160453c8a59)
![{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left[\left(J^{-2/3}~{\frac {\ частичный W}{\partial {\bar {I}}_{1}}}+J^{-2/3}~{\bar {I}}_{1}~{\frac {\partial W}{ \partial {\bar {I}}_{2}}}\right)~{\boldsymbol {B}}-J^{-4/3}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\\&\qquad 2~J~\left[-{\frac {1} {3}}~J^{-2}~\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}} }+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)+{\frac {1} {2}}~J^{-1}~{\frac {\partial W}{\partial J}}\right]~{\boldsymbol {\mathit {1}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92fc8cc0a376769e1a55384831822bfe7278570)
![{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left[{\frac {1}{J^{2/3}}}~ \left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial W}{\ частичный {\bar {I}}_{2}}}\right)~{\boldsymbol {B}}-{\frac {1}{J^{4/3}}}~{\frac {\partial W }{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]\\&\qquad +\left[{\frac { \partial W}{\partial J}}-{\frac {2}{3J}}\left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\ right)\right]{\boldsymbol {\mathit {1}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33fb2175d1cf8867bc4aeb7f3991b4d237cf1543)
![{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\frac {2}{J}}~\left[\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right) ~{\bar {\boldsymbol {B}}}-{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\ cdot {\bar {\boldsymbol {B}}}\right]\\&\qquad +\left[{\frac {\partial W}{\partial J}}-{\frac {2}{3J}}\ left({\bar {I}}_{1}~{\frac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{ 2}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)\right]{\boldsymbol {\mathit {1}}}\end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bab10de5208332a92b44c2e19af8c19a8dca207)
![{\displaystyle {\boldsymbol {\sigma }}=2\left[\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+I_{1}~{ \frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\frac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]-p~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e5f43a4b8e83bf20b8c88b401395570654aaa89)
![{\displaystyle {\begin{aligned}{\frac {\partial W}{\partial {\boldsymbol {C}}}} &={\frac {\partial W}{\partial \lambda _{1}}} ~{\frac {\partial \lambda _{1}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial \lambda _{2}}}~{\frac {\partial \lambda _{2}}{\partial {\boldsymbol {C}}}}+{\frac {\partial W}{\partial \lambda _{3}}}~{\frac {\partial \ лямбда _{3}}{\partial {\boldsymbol {C}}}}\\&={\boldsymbol {R}}^{T}\cdot \left[{\frac {1}{2\lambda _{ 1}}}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac { 1}{2\lambda _{2}}}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _ {2}+{\frac {1}{2\lambda _{3}}}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3} \otimes \mathbf {n} _{3}\right]\cdot {\boldsymbol {R}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/376db081f7668da0294fb408efd68f30e246fba8)
![{\displaystyle {\boldsymbol {\sigma }}={\frac {2}{J}}~{\boldsymbol {V}}\cdot \left[{\frac {1}{2\lambda _{1}} }~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\frac {1} 2\lambda _{2}}}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2} +{\frac {1}{2\lambda _{3}}}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \ mathbf {n} _{3}\right]\cdot {\boldsymbol {V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c1cbf72e429aed44eb8dfa08ee2108ef209c94b)
![{\displaystyle {\boldsymbol {\sigma }}={\frac {1}{\lambda _{1}\lambda _{2}\lambda _{3}}}~\left[\lambda _{1}~ {\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\ frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac { \partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32b4bfca4342f7dc22085470c19916ece1ea702b)
![{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&=-p~{\boldsymbol {\mathit {1}}}+2\left[\left({\frac {\partial {\hat {W}}}{\partial I_{1}}}+I_{1}~{\frac {\partial {\hat {W}}}{\partial I_{2}}}\right){\boldsymbol { B}}-{\frac {\partial {\hat {W}}}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]\\& = -p~{\boldsymbol {\mathit {1}}}+2\left[\left({\frac {\partial W}{\partial {\bar {I}}_{1}}}+I_{ 1}~{\frac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\frac {\partial W }{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]\\&=- p~{\boldsymbol {\mathit {1}}}+\lambda _{1}~{\frac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1} \otimes \mathbf {n} _{1}+\lambda _{2}~{\frac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\frac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec076b6ccffceae7e2ba84414d011247098baac)
![{\displaystyle W={\tfrac {1}{2}}\lambda ~[\mathrm {tr} ({\boldsymbol {\varepsilon }})]^{2}+\mu ~\mathrm {tr} {\ маторд {\left({\boldsymbol {\varepsilon }}^{2}\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bcd60974de818734aa8e47cea766e49c221fc7e)
