stringtranslate.com

Ортоцентроидальная окружность

Треугольник (черный), его ортоцентр (синий), его центроид (красный) и его ортоцентроидный диск (желтый)
  Ортоцентроидальная окружность, ограниченная ортоцентром ( H) и центроидом (S)
  Прямая Эйлера , на которой центр описанной окружности (O) и центр девяти точек (N) лежат вместе с точками H и S
  F 1 и F 2 : точки Ферма
  F: Точка Фейербаха
  I: Инцентр
  G: точка Жергонна
  U: Точка симедианы

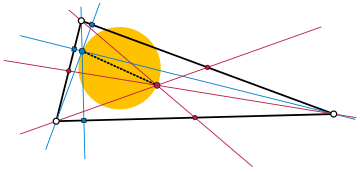
В геометрии ортоцентроидная окружность неравностороннего треугольника — это окружность, ортоцентр и центроид которой находятся на противоположных концах ее диаметра . Этот диаметр также содержит центр треугольника с девятью точками и является подмножеством прямой Эйлера , которая также содержит центр описанной окружности вне ортоцентроидной окружности.

Эндрю Гинанд показал в 1984 году, что инцентр треугольника должен лежать внутри ортоцентроидальной окружности, но не совпадать с центром девяти точек; то есть он должен попадать в открытый ортоцентроидальный диск , проколотый в центре девяти точек. [1] [2] [3] [4] [5] : стр. 451–452  Инцентром может быть любая такая точка, в зависимости от конкретного треугольника, имеющего этот конкретный ортоцентроидальный диск. [3]

Более того, [2] точка Ферма , точка Жергонна и точка симмедианы находятся в открытом ортоцентроидальном диске, проколотом в его собственном центре (и могут находиться в любой точке внутри него), в то время как вторая точка Ферма и точка Фейербаха находятся во внешней части ортоцентроидального круга. Множество потенциальных местоположений одной или другой точки Брокара также является открытым ортоцентроидальным диском. [6]

Квадрат диаметра ортоцентроидальной окружности равен [7] : стр.102  , где a, b и c — длины сторон треугольника, а D — диаметр описанной окружности .

Ссылки

  1. ^ Guinand, Andrew P. (1984), «Линии Эйлера, центры трикасательных треугольников и их треугольники», American Mathematical Monthly , 91 (5): 290–300, doi :10.2307/2322671, JSTOR  2322671.
  2. ^ ab Брэдли, Кристофер Дж.; Смит, Джефф К. (2006), «Расположение центров треугольников», Forum Geometricorum , 6 : 57–70.
  3. ^ ab Stern, Joseph (2007), «Проблема определения треугольника Эйлера» (PDF) , Forum Geometricorum , 7 : 1–9.
  4. ^ Францсен, Уильям Н. (2011), «Расстояние от инцентра до линии Эйлера», Forum Geometricorum , 11 : 231–236.
  5. ^ Леверша, Джерри; Смит, GC (ноябрь 2007 г.), «Эйлер и геометрия треугольника», Mathematical Gazette , 91 (522): 436–452, doi :10.1017/S0025557200182087, JSTOR  40378417, S2CID  125341434.
  6. ^ Брэдли, Кристофер Дж.; Смит, Джефф К. (2006), «Расположение точек Брокара», Forum Geometricorum , 6 : 71–77.
  7. ^ Альтшиллер-Корт, Натан, College Geometry , Dover Publications, 2007 (оригинал Barnes & Noble 1952).

Внешние ссылки