Роторная динамика

Раздел прикладной механики, изучающий вращающиеся конструкции

Ротородинамика (или динамика ротора ) — специализированная отрасль прикладной механики, занимающаяся поведением и диагностикой вращающихся конструкций. Она обычно используется для анализа поведения конструкций, начиная от реактивных двигателей и паровых турбин и заканчивая автомобильными двигателями и компьютерными дисковыми накопителями . На самом базовом уровне динамика ротора связана с одной или несколькими механическими конструкциями ( роторами ), поддерживаемыми подшипниками и находящимися под влиянием внутренних явлений, которые вращаются вокруг одной оси . Опорная конструкция называется статором . По мере увеличения скорости вращения амплитуда вибрации часто проходит через максимум, который называется критической скоростью . Эта амплитуда обычно возбуждается дисбалансом вращающейся конструкции; повседневные примеры включают балансировку двигателя и балансировку шин . Если амплитуда вибрации на этих критических скоростях чрезмерна, то происходит катастрофический отказ . В дополнение к этому, турбомашины часто развивают нестабильности, которые связаны с внутренним составом турбомашин и которые необходимо исправить. Это главная забота инженеров, которые проектируют большие роторы.

Вращающееся оборудование производит вибрации в зависимости от структуры механизма, участвующего в процессе. Любые неисправности в машине могут увеличить или возбудить сигнатуры вибрации. Вибрационное поведение машины из-за дисбаланса является одним из основных аспектов вращающегося оборудования, который необходимо подробно изучить и учитывать при проектировании. Все объекты, включая вращающееся оборудование, демонстрируют собственную частоту в зависимости от структуры объекта. Критическая скорость вращающегося оборудования возникает, когда скорость вращения совпадает с его собственной частотой. Самая низкая скорость, при которой впервые встречается собственная частота, называется первой критической скоростью, но по мере увеличения скорости появляются дополнительные критические скорости, которые являются кратными собственной частоте. Следовательно, минимизация вращательного дисбаланса и ненужных внешних сил очень важна для снижения общих сил, которые инициируют резонанс . Когда вибрация находится в резонансе, она создает разрушительную энергию, которая должна быть главной заботой при проектировании вращающегося оборудования. Цель здесь должна заключаться в том, чтобы избегать операций, которые близки к критическим, и безопасно проходить через них при ускорении или замедлении. Если этот аспект игнорировать, это может привести к потере оборудования, чрезмерному износу машин, катастрофическим поломкам, не подлежащим ремонту, или даже к человеческим травмам и гибели людей.

Реальную динамику машины трудно смоделировать теоретически. Расчеты основаны на упрощенных моделях, которые напоминают различные структурные компоненты ( модели с сосредоточенными параметрами ), уравнениях, полученных из численного решения моделей ( метод Рэлея–Ритца ) и, наконец, на методе конечных элементов (FEM), который является другим подходом к моделированию и анализу машины для собственных частот. Существуют также некоторые аналитические методы, такие как метод распределенной передаточной функции ^[1] , который может генерировать аналитические и замкнутые формы собственных частот, критические скорости и реакцию неуравновешенной массы. На любом прототипе машины он тестируется для подтверждения точных частот резонанса, а затем перепроектируется, чтобы гарантировать, что резонанс не возникнет.

Основные принципы

Уравнение движения в обобщенной матричной форме для аксиально-симметричного ротора, вращающегося с постоянной скоростью вращения Ω, имеет вид: $${\displaystyle \mathbf {M} {\ddot {\mathbf {q} }}(t)+(\mathbf {C} +\mathbf {G} ){\dot {\mathbf {q} }}(t)+(\mathbf {K} +\mathbf {N} )\mathbf {q} (t)=\mathbf {f} (t)}$$

M — симметричная матрица масс ;

C — симметричная матрица затухания ;

G — кососимметричная гироскопическая матрица:

K — симметричная матрица жесткости подшипника или уплотнения;

N — гироскопическая матрица отклонения для включения, например, центробежных элементов;

q ( ​​t ) — обобщенные координаты ротора в инерциальных координатах;

f ( t ) — вынуждающая функция, обычно включающая дисбаланс.

Гироскопическая матрица G пропорциональна скорости вращения Ω . Общее решение приведенного выше уравнения включает в себя комплексные собственные векторы , зависящие от скорости вращения. Инженерные специалисты в этой области полагаются на диаграмму Кэмпбелла для исследования этих решений.

Интересной особенностью роторно-динамической системы уравнений являются недиагональные члены жесткости, демпфирования и массы. Эти члены называются перекрестно-связанной жесткостью, перекрестно-связанным демпфированием и перекрестно-связанной массой. Когда есть положительная перекрестно-связанная жесткость, отклонение вызовет силу реакции, противоположную направлению отклонения, чтобы отреагировать на нагрузку, а также силу реакции в направлении положительного завихрения. Если эта сила достаточно велика по сравнению с доступным прямым демпфированием и жесткостью, ротор будет нестабильным. Когда ротор нестабилен, обычно требуется немедленное отключение машины, чтобы избежать катастрофического отказа.

ротор Джеффкотта

Ротор Джеффкотта (названный в честь Генри Хомана Джеффкотта), также известный в Европе как ротор Лаваля , представляет собой упрощенную модель с сосредоточенными параметрами, используемую для решения этих уравнений. Ротор Джеффкотта состоит из гибкого, безмассового, однородного вала, установленного на двух гибких подшипниках, равноудаленных от массивного диска, жестко прикрепленного к валу. Простейшая форма ротора ограничивает диск плоскостью, ортогональной оси вращения. Это ограничивает реакцию ротора только на боковую вибрацию. Если диск идеально сбалансирован (т. е. его геометрический центр и центр масс совпадают), то ротор аналогичен незатухающему осциллятору с одной степенью свободы при свободных колебаниях. Если между геометрическим центром и центром масс есть некоторое радиальное расстояние, то ротор неуравновешен, что создает силу, пропорциональную массе диска m , расстоянию между двумя центрами (эксцентриситету, ε ) и скорости вращения диска Ω . После вычисления эквивалентной жесткости системы k мы можем составить следующее линейное обыкновенное дифференциальное уравнение второго порядка, которое описывает радиальное отклонение диска от центральной линии ротора. ^[2]

$${\displaystyle m\mathbb {\ddot {r}} +k\mathbb {r} =m\varepsilon \Omega ^{2}\sin(\Omega t)}$$

Если бы мы изобразили радиальный отклик, мы бы увидели синусоидальную волну с угловой частотой . Это боковое колебание называется «вихрем» и в этом случае сильно зависит от скорости вращения. Скорость вращения не только влияет на амплитуду функции силы, но и может вызывать динамическое усиление вблизи собственной частоты системы. ${\displaystyle \Omega /2\pi }$

Хотя ротор Джеффкотта является полезным инструментом для введения концепций роторной динамики, важно отметить, что это математическая идеализация , которая лишь приблизительно аппроксимирует поведение реальных роторов. ^[2]

Диаграмма Кэмпбелла

Диаграмма Кэмпбелла для простого ротора

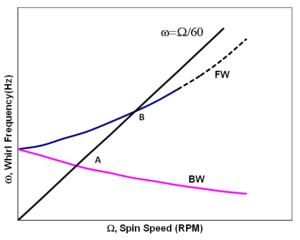
Диаграмма Кэмпбелла , также известная как «Карта скорости вращения» или «Диаграмма частотной интерференции», простой роторной системы показана справа. Розовая и синяя кривые показывают режимы обратного вращения (BW) и прямого вращения (FW) соответственно, которые расходятся по мере увеличения скорости вращения. Когда частота BW или частота FW равна скорости вращения Ω, обозначенной пересечениями A и B с линией синхронной скорости вращения, реакция ротора может показать пик. Это называется критической скоростью .

История

История роторной динамики изобилует взаимодействием теории и практики. WJM Rankine впервые выполнил анализ вращающегося вала в 1869 году, но его модель оказалась неадекватной, и он предсказал, что сверхкритические скорости не могут быть достигнуты. В 1895 году Dunkerley опубликовал экспериментальную работу, описывающую сверхкритические скорости. Gustaf de Laval , шведский инженер, разогнал паровую турбину до сверхкритических скоростей в 1889 году, а Kerr опубликовал работу, демонстрирующую экспериментальное доказательство второй критической скорости в 1916 году.

Генри Джеффкотт был уполномочен Лондонским королевским обществом разрешить конфликт между теорией и практикой. Он опубликовал статью, которая теперь считается классической, в Philosophical Magazine в 1919 году, в которой он подтвердил существование стабильных сверхкритических скоростей. Август Фёппль опубликовал почти такие же выводы в 1895 году, но история в значительной степени проигнорировала его работу.

Между работой Джеффкотта и началом Второй мировой войны было много работы в области неустойчивостей и методов моделирования, кульминацией которой стала работа Нильса Отто Мюклестада ^[3] и М.А. Проля ^[4] , которая привела к методу матрицы переноса (TMM) для анализа роторов. Наиболее распространенным методом, используемым сегодня для анализа роторной динамики, является метод конечных элементов .

Современные компьютерные модели были прокомментированы в цитате, приписываемой Даре Чайлдс: «Качество прогнозов компьютерного кода в большей степени связано с надежностью базовой модели и физическим пониманием аналитика ... Более совершенные алгоритмы или компьютерные коды не исправят плохие модели или недостаток инженерного суждения».

Профессор Ф. Нельсон много писал по истории роторной динамики, и большая часть этого раздела основана на его работах.

Программное обеспечение

Существует множество программных пакетов, способных решать систему уравнений динамики ротора. Коды, специфичные для динамики ротора, более универсальны для целей проектирования. Эти коды позволяют легко добавлять коэффициенты подшипников, боковые нагрузки и многие другие элементы, которые могут понадобиться только специалисту по динамике ротора. Коды, специфичные для динамики не ротора, являются полнофункциональными решателями FEA и имеют многолетнюю разработку в своих методах решения. Коды, специфичные для динамики не ротора, также могут использоваться для калибровки кода, разработанного для динамики ротора.

Смотрите также

• Ось
• Балансировочный станок
• Подшипник (механический)
• Приводной вал
• Экзоскелетный двигатель
• Магнитный подшипник
• Турбина

Ссылки

• Chen, WJ, Gunter, EJ (2005). Введение в динамику систем роторных подшипников . Victoria, BC: Trafford. ISBN 978-1-4120-5190-3.{{cite book}}: CS1 maint: multiple names: authors list (link)использует DyRoBeS
• Чайлдс, Д. (1993). Явления роторной динамики турбомашин, моделирование и анализ . Wiley. ISBN 978-0-471-53840-0.
• Фредерик Ф. Эрих, ред. (1992). Справочник по роторной динамике . McGraw-Hill. ISBN 978-0-07-019330-7.
• Genta, G. (2005). Динамика вращающихся систем . Springer. ISBN 978-0-387-20936-4.
• Джеффкотт, ХХ (1919). «Валы, нагруженные поперечной вибрацией в окрестности вращательной скорости. — Эффект недостатка равновесия». Philosophical Magazine . 6. 37 .
• Кремер, Э. (1993). Динамика роторов и фундаментов . Спрингер-Верлаг. ISBN 978-0-387-55725-0.
• Лаланн, М., Феррарис, Г. (1998). Прогнозирование роторной динамики в машиностроении, второе издание . Wiley. ISBN 978-0-471-97288-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Мушиньска, Агнешка (2005). Роторная динамика . ЦРК Пресс. ISBN 978-0-8247-2399-6.
• Нельсон, Ф. (июнь 2003 г.). «Краткая история ранней роторной динамики». Звук и вибрация .
• Нельсон, Ф. (июль 2007 г.). «Роторная динамика без уравнений». Международный журнал COMADEM . 3. 10. ISSN 1363-7681  .
• Нельсон, Ф. (2011). Введение в роторную динамику . Том SVM-19 [1]. {{cite book}}: Внешняя ссылка в |volume=( помощь )
• Лаланн, М., Феррарис, Г. (1998). Прогнозирование роторной динамики в машиностроении, второе издание . Wiley. ISBN 978-0-471-97288-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Вэнс, Джон М. (1988). Роторная динамика турбомашин . Wiley. ISBN 978-0-471-80258-7.
• Тивари, Раджив (2017). Роторные системы: анализ и идентификация . CRC Press. ISBN 9781138036284.
• Вэнс, Джон М., Мерфи, Б., Зейдан, Ф. (2010). Вибрация машин и роторная динамика . Wiley. ISBN 978-0-471-46213-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Vollan, A., Komzsik, L. (2012). Вычислительные методы динамики ротора с использованием метода конечных элементов . CRC Press. ISBN 978-1-4398-4770-1.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Ямамото, Т., Ишида, И. (2001). Линейная и нелинейная роторная динамика . Wiley. ISBN 978-0-471-18175-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Ганеривала, С., Мохсен Н. (2008). Анализ динамики ротора с использованием XLRotor. SQI03-02800-0811

Примечания

1. Лю, Шибинг; Ян, Бинген (2017-02-22). «Вибрации гибких многоступенчатых роторных систем, поддерживаемых резиновыми подшипниками с водяной смазкой». Журнал вибрации и акустики . 139 (2): 021016–021016–12. doi :10.1115/1.4035136. ISSN  1048-9002.
2. Мацусита, Осами; Танака, Масато; Канки, Хироши; Кобаяши, Масао; Кио, Патрик (2017). Вибрации вращающихся машин (1-е изд.). Япония: Спрингер. стр. 199–206. ISBN 978-4-431-55455-4.
3. Myklestad, Nils (апрель 1944 г.). «Новый метод расчета собственных форм несвязанных изгибных колебаний крыльев самолета и других типов балок». Журнал авиационных наук (Институт авиационных наук) . 11 (2): 153–162. doi :10.2514/8.11116.
4. Prohl, MA (1945), «Общий метод расчета критических скоростей гибких роторов», Trans ASME , 66 : A–142
5. "ROTORDYNAMICS OF TURBOMACHINERY, Software and Engineering services, Alfa-Tranzit Co". www.alfatran.com . Получено 2022-01-11 .
6. "AxSTREAM - Rotordynamics | Turbomachinery Design Software". www.softinway.com . 2016-07-27 . Получено 2022-01-11 .
7. "Главная". www.fem.unicamp.br . Получено 2022-01-11 .
8. "Анализ динамики ротора: SAMCEF Rotors справляется с задачей". Архивировано из оригинала 29-09-2012 . Получено 04-06-2013 .
9. "Главная". www.madyn.de . Получено 2022-01-11 .
10. "MADYN 2000 для роторной динамики". www.delta-js.ch . Получено 2022-01-11 .
11. "Архивная копия". Архивировано из оригинала 2021-05-07 . Получено 2022-01-11 .{{cite web}}: CS1 maint: archived copy as title (link)
12. "FEMRDYN". dynatechengr.com . Получено 2022-01-11 .
13. "Dyrobes – революция в программном обеспечении для динамики роторов" . Получено 11.01.2022 .
14. "RITEC - RIMAP (Rotordynamic Analysis Software Package)". Архивировано из оригинала 2013-10-04 . Получено 2013-10-01 .
15. "Главная". XLRotor . Получено 2022-01-11 .
16. "ARMD Rotor Dynamics" . Получено 2022-01-01 .
17. "Лаборатория турбомашиностроения". turbolab.tamu.edu . Получено 2022-01-11 .
18. «Лаборатория вращающихся машин и механизмов управления».
19. "Институт гидродинамических машин имени Шевальского". Архивировано из оригинала 2008-12-15.
20. "D&M; Technology Co., Ltd". Архивировано из оригинала 2021-05-06.
21. "LaMCoS". lamcos.insa-lyon.fr . Получено 2022-01-11 .
22. "Программное обеспечение Rotordynamics для предиктивного анализа вращающихся машин". www.comsol.com . Получено 2022-01-11 .
23. "Rotordynamics-Seal Research - RSR". rda.guru . Получено 2022-01-11 .

Внешние ссылки

• Анализ динамики ротора с использованием XLRotor
• Вход в техническую литературу по роторной динамике